1.Построить логарифмические характеристики заданного элемента.

2.Последовательность операций при построении характеристик корректирующих устройств.

Пусть задана неизменяемая часть следящей системы с передаточной функцией

.

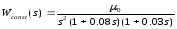Нетрудно обнаружить, что система с такой передаточной функцией неработоспособна, ибо она попросту неустойчива. В самом деле, при замыкании жесткой обратной связью справедливо характеристическое уравнение

.

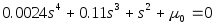Неустойчивость обнаруживается с помощью любого критерия. На рис.12.1 показана амплитудная частотная характеристика (на оси абсцисс указаны десятичные логарифмы частоты).

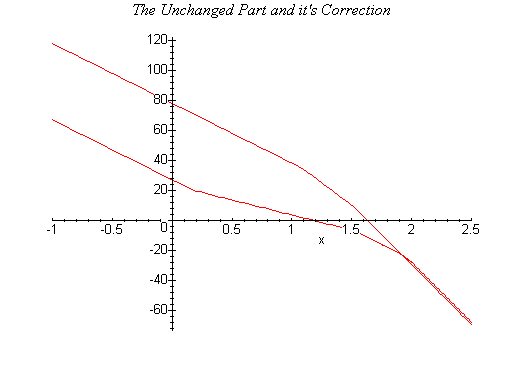
В данном случае нет необходимости строить фазовую характеристику, т.к. из-за наличия полюса второго порядка в передаточной функции неизменяемой части и отсутствию дифференцирующих элементов, она полностью находится ниже линии –180^о. При любом значении коэффициента усиления происходит охват критической точки –1. Сохраняя второй порядок астатизма системы, построим желаемую характеристику с частотой среза около 15 с^-1 (на оси частот ей соответствует отсчет 1.18). Прежде всего, найдем точку пересечения низкочастотной и средне- частотной асимптот. Пусть по условиям точности необходима добротность 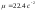. Тогда уравнение низкочастотной асимптоты выражается прямой

.

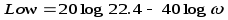Очевидно, среднечастотная асимптота, удовлетворяющая условию оптимальности в смысле быстродействия, имеет аналитическое выражение

.

Обе прямые пересекаются при частоте, определяемой равенством

,

.

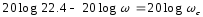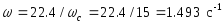В этой точке происходит излом амплитудной частотной характеристики, наклон становится равным –20 дБ/дек (рис.12.1) .

Поскольку неизменяемая часть в области высоких частот имеет характеристику с наклоном –80 дБ/дек, то и желаемую характеристику с помощью кусочно-линейной аппроксимации следует привести к такому же наклону.

Соответствующая передаточная функция имеет вид

. (12.1)

Для проверки устойчивости скорректированной системы можно построить ФХ или составить определитель Гурвица для характеристического уравнения

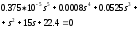
и убедиться, что все его диагональные миноры положительны.

Рис.12.2. Схема для вычисления передаточной функции Z(s).

Найдем передаточную функцию корректирующего элемента, если он подсоединен так, как показано на рис.12.2. Поскольку нам неизвестны пока ни вид, ни, тем более, количественные значения параметров корректирующего элемента, постараемся найти его характеристики, не используя приближенных соотношений типа (11.6).

Желаемая передаточная функция (12.1) согласно схеме равна

.

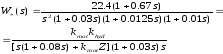Отсюда нетрудно найти передаточную функцию

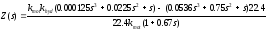.С помощью усилителя можно так изменить произведение 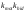, чтобы выполнялось условие.

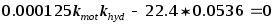
Этим мы реализуем корректирующую цепь наиболее просто, ибо в числителе исчезнет третья степень s. Таким образом,

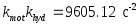и

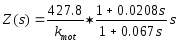. (12.2)

Корректирующий элемент с передаточной функцией (12.2) вполне реализуем в виде тахогенератора, напряжение с которого поступает на пассивную интегро-дифференцирующую цепь (рис.12.3).

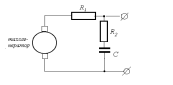
Рис.12.3. Реализация корректирующего элемента с помощью тахогенератора и пассивной RC-цепи.

3.Использование простых итераций при анализе нелинейных систем. Условия сходимости итераций.

Решение можно получить с любой точностью, воспользовавшись методом последовательных приближений. В частности, можно использовать легко реализуемый метод - простых итераций. Следует лишь отметить, что условия сходимости этого метода не всегда выполняются, поэтому есть смысл рассмотреть общие условия его сходимости.

Пусть требуется решить уравнение вида 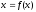, (21.6)где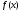- некоторая функция, допускающая существование первой производной. Метод простых итераций строится по формуле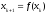(21.7)

Теорема

Если в интервале, содержащем корень уравнения (21.6),а также все последовательные приближения, получаемые по формуле (21.7), выполняется условие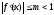, (21.8) то.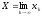

Доказательство

По определению 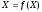. Согласно процедуре итераций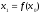. Следовательно,

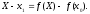
Или, согласно известной теореме Лагранжа,,

где 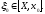Аналогичным путем получаем последовательность оценок

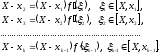
Перемножив оценки, после сокращений находим .

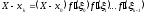При выполнении условия (21.8) теоремы получаем 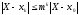(21.9)

Переходя в (21.9) к пределу при 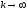, получаем утверждение теоремы.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 8