3.Типы особых точек фазового пространства.

1.Корни вещественные и одного знака. Обозначив их отношение буквой n, получаем семейство степенных зависимостей 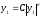. (19.9)

На рис.19.1 изображено семейство графиков для случая n=2 и для различных значений постоянной интегрирования C .

Рис.19.1. Особая точка типа «узел».

Поскольку через начало координат проходит бесчисленное множество фазовых траекторий, эта точка является особой и в данном случае имеет название «узел». Если оба корня отрицательны, узел является устойчивым. При возрастании времени изображающая точка вдоль каждой траектории приближается к особой точке. В случае положительных корней узел неустойчив.

2.Корни вещественны и разных знаков. В этом случае показатель степени в формуле (19.9) отрицателен, что соответствует кривым гиперболического типа. Такая точка называется «седло» Седло всегда неустойчиво, ибо все траектории проходят мимо особой точки. Исключение составляет одна из координатных осей. Однако при любом сколь угодно малом отклонении начальных условий, уводящих изображающую точку от оси, мы получаем одну из гиперболических кривых.

Рис.19.2.Фазовые траектории в окрестности точки типа «седло».

3.Корни комплексные сопряженные. Пусть 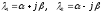. Особая точка в этом случае называется фокусом, устойчивым или неустойчивым в зависимости от знака  .

4.Корни мнимые. В этом случае особая точка называется центром.

Фазовые траектории представляются семейством эллипсов вокруг этой точки (рис.19.4).

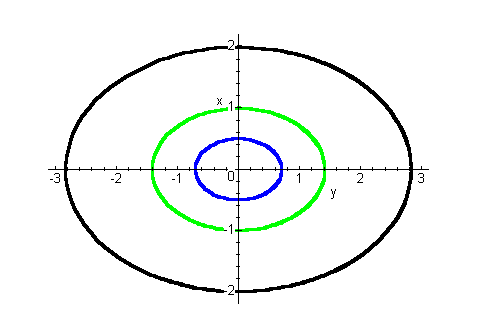
Рис.19.4. Фазовые траектории в окрестности особой точки типа «центр».

5.Корни кратные и матрица системы приводится к диагональной форме.

Дифференциальное уравнение фазовых траекторий имеет в этом случае 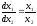, интегрирование которого не вызывает затруднений и приводит к совокупности прямых, проходящих через начало.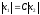

Особая точка называется дикритический узел.

6. корни кратные, но матрица системы приводится к клетке Жордана второго порядка .

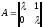уравнение фазовой траектории .

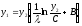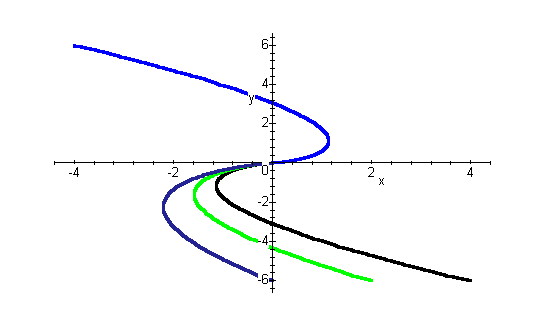
Рис.19.5. Фазовые траектории в окрестности точки типа «вырожденный узел»

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 4

1.Передаточная функция линейной динамической системы. Классификация элементов.

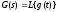Обозначая для краткости и, имеем.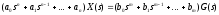

Найдем отношение (2.18)

Мы получили выражение для передаточной функции линейной динамической системы, которая в соответствии с выражением (1.3) обозначается тем же символом, что и частотный оператор.

Определение

Передаточной функцией линейной динамической системы называется отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях.

Рассмотрим знаменатель передаточной функции (2.18).Согласно известной теореме из алгебры целый многочлен можно разложить на элементарные сомножители 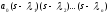, где- корни знаменателя, которые могут либо вещественными числами, либо комплексными попарно сопряженными. Рассмотрим далее отдельные случаи.

1.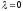. Передаточная функция элемента имеет вид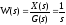(3.1)

Элемент, обладающий такой передаточной функцией, называется интегрирующим. Действительно, из (3.1) вытекает в соответствии

С теоремой об изображении производно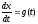й или.

2. , где- вещественный параметр(постоянная времени элемента). В этом случае элемент обладает передаточной функцией. (3.2) Элемент называетсяапериодическим. Действительно, при входном тестовом воздействии типа единичной ступеньки . Переходя к оригиналам, имеем.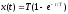

3.Пара комплексно-сопряженных корней .

Передаточная функция имеет вид

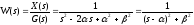
Обращаясь к формуле 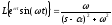,полученной нами на лекции 2, и полагая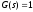(изображение единичного импульса), имеем.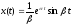

Элемент называется колебательным. Как видим, реакция элемента на тестовое воздействие типа импульса представляет собой затухающую синусоиду (при 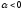).В технической литературе по автоматическому управлению принято записывать передаточную функцию колебательного элемента в несколько иной форме. Введем обозначения

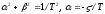, запишем (с точностью до постоянного множителя 1/T²) 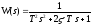. (3.3)

Такая форма записи передаточной функции колебательного элемента называется канонической (свободный член в знаменателе равен единице). Параметр T называется постоянной времени колебательного элемента, параметр 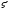называетсякоэффициентом демпфирования.

Перейдем теперь к числителю передаточной функции

4 в случае вещественного корня. (3.4)

передаточную функцию дифференцирующего элемента первого порядка.

5 В случае пары комплексных корней имеем (3.5) передаточную функцию дифференцирующего элемента второго порядка.

6.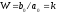Элемент, обладающий такой передаточной функцией, называетсяусилительным независимо от величины коэффициента усиления k.