
- •1.Методы математического описания линейных систем управления.
- •2.Связь между частотными критериями устойчивости и методами выделения области устойчивости в пространстве параметров.
- •3.Аналитическое описание нелинейных элементов. Кусочно-линейная аппроксимация.
- •1.Типовые тестовые воздействия и их краткая характеристика.
- •2.Импульсная переходная характеристика линейной системы управления.
- •3.Метод фазового пространства исследования нелинейных систем.
- •1.Периодические и непериодические сигналы. Преобразование Лапласа.
- •2.Коэффициенты ошибок следящих систем.
- •3.Типы особых точек фазового пространства.
- •1.Передаточная функция линейной динамической системы. Классификация элементов.
- •2.Каким порядком астатизма должна обладать следящая система, чтобы при входном воздействии вида tn установившаяся ошибка была равна нулю?
- •3.Исследование следящей системы с нелинейным элементом типа «линейная зона с участками насыщения».
- •1.Общий вид дифференциального уравнения многомерной системы управления.
- •2.Оптимальный переходный процесс. Возможности реализации.
- •3.Исследование релейной следящей системы методом фазового пространства.
- •1.Годограф частотного оператора системы автоматического управления.
- •2. Синтез следящей системы с заданными показателями качества.
- •3.Исследование релейной следящей системы с гистерезисом.
- •1.Построить логарифмические характеристики заданного элемента.
- •2.Последовательность операций при построении характеристик корректирующих устройств.
- •3.Использование простых итераций при анализе нелинейных систем. Условия сходимости итераций.
- •1.Написать передаточную функцию по заданному графику амплитудной частотной характеристики.
- •2.Интегральная квадратическая оценка качества переходного процесса.
- •1.Построить логарифмическую частотную характеристику замкнутой следящей системы по заданному графику разомкнутой.
- •2.Интегральная оценка переходного процесса с экспоненциальным сглаживанием.
- •3. Исследование релейного автопилота. Скользящий режим.
- •1.Преобразование многоконтурных структурных схем.
- •2.Алгоритм поиска минимума интегральной оценки в пространстве параметров.
- •3.Метод гармонической линеаризации. Вычисление коэффициентов.
- •1.Записать передаточную функцию при заданной структурной схеме.
- •2.Связь между качеством переходного процесса и распределением нулей и полюсов передаточной функции.
- •3.Гармоническая линеаризация идеального реле.
- •1.Определение устойчивости движения по а.М. Ляпунову.
- •2.Способы модуляции в дискретных системах управления.
- •3.Аналитическое исследование автоколебаний при гармонической линеаризации.
- •1.Теорема а.М. Ляпунова об устойчивости для систем, допускающих линеаризацию.
- •2.Рекуррентные соотношения в дискретных системах управления.
- •3.Частотный подход к анализу автоколебаний.
- •1.Практическое применение критерия устойчивости Гурвица (не ниже 4-го порядка)..
- •2.Модификация критерия Гурвица для дискретных систем.
- •1.Доказать критерий устойчивости а.В. Михайлова.
- •2.Управляемость динамических систем. Теорема Калмана об управляемости.
- •3.Вынужденные колебания в нелинейных системах. Условия существования.
- •1.Доказать критерий устойчивости Найквиста.
- •2.Наблюдаемость динамических систем. Теорема Калмана о наблюдаемости.
- •3.Вынужденные колебания в нелинейных системах. Пороговая амплитуда возбуждающего сигнала. Вибрационное сглаживание разрывных характеристик.
- •2.Какое влияние оказывает элемент с запаздыванием на характеристики системы управления?
- •3.Качественный анализ переходных процессов в нелинейных системах, описываемых уравнениями высокого порядка.
- •1.В чем состоит основной принцип выделения границ области устойчивости в пространстве параметров?
- •2.Изложить аналитический подход к исследованию многомерной системы управления. Распространение понятия свертки на многомерные системы.
- •3.Выделение зон затухания и возрастания амплитуды автоколебаний нелинейных систем до установившегося значения.
- •1.Выделение области устойчивости в пространстве двух параметров. Особые прямые. Правила штриховки границы.
- •2.Сформулировать условия устойчивости линейной системы управления с медленно меняющимися параметрами.
- •3.Знакоопределенные и знакопостоянные функции. Связь с устойчивостью нелинейных систем.
- •1.Теорема а.М. Ляпунова об устойчивости в общем случае (с использованием знакоопределенных функций).
- •2.Анализ устойчивости релейной следящей системы с помощью функций а.М. Ляпунова.
- •3.Анализ устойчивости автопилота с нелинейным исполнительным элементом. Абсолютная устойчивость.
- •1.Общие приемы исследования нелинейных систем произвольного порядка.
- •2.Теоремы а.М. Ляпунова об асимптотической устойчивости и о неустойчивости.
- •1.Примеры элементов с нелинейными характеристиками.
- •2.Псевдолинейная коррекция частотных характеристик.
- •3.Преобразоание уравнения высокого порядка, описывающего линейную систему управления к нормальной системе в форме Коши.
1.Доказать критерий устойчивости а.В. Михайлова.
Критерий
Михайлова был
разработан в 30-х г.г. ХХ столетия. Для
его вывода рассмотрим характеристический
полином,
т.е. выражение вида
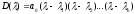 ,
(8.1)
,
(8.1)
в
котором положим
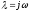 ,
и проследим за изменением аргумента
вектора
,
и проследим за изменением аргумента
вектора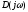 при
при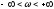 .
Очевидно, изменение аргумента отдельных
сомножителей в (8.1) будет зависеть от
того, в какой части плоскости расположен
корень (рис.8.1). Это изменение
.
Очевидно, изменение аргумента отдельных
сомножителей в (8.1) будет зависеть от
того, в какой части плоскости расположен
корень (рис.8.1). Это изменение
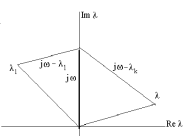
Рис.8.1. Расположение корней характеристического полинома
будет
равно 180о
, если корень расположен в левой
полуплоскости и –180о
в противоположном случае. Таким образом,
приращение аргумента вектора
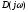 равно
равно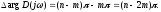
Здесь
m
– число корней с положительной
действительной частью. Если все корни
характеристического полинома имеют
отри-цательную вещественную часть, то
изменение аргумента характеристического
полинома составит
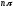
Этот
критерий обычно формулируется несколько
иначе. Если принять во внимание, что
годограф характеристического полинома
симметричен относительно вещественной
оси, то достаточно проследить за
изменением его аргумента лишь при
положительных значениях частоты. При
m=0
оно составит
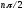 .
Иными словами:
.
Иными словами:
для того, чтобы характеристический полином (8.1) имел все корни с отрицательной вещественной частью необходимо, чтобы его годограф монотонно проходил n квадрантов комплексной плоскости.
2.Управляемость динамических систем. Теорема Калмана об управляемости.
запишем
соответствующее дифференциальное
уравнение в наиболее общем виде
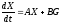 .
.
Здесь X=( x1,x2,…xn ) T – вектор состояния, G=( g1,g2,…gm) T – вектор управления,A - квадратная матрица порядка n.
В
соответствии с введенными обозначениями
матрица
 ,
не обязательно квадратная и некоторые
ее элементы могут быть нулями
,
не обязательно квадратная и некоторые
ее элементы могут быть нулями
Некоторые
компоненты вектора X
или их линейные комбинации можно
измерить. Совокупность измеренных
координат мы будем обозначать вектором
Y
= ( y1,y2,…yq
) T
, а его связь с компонентами вектора
состояния выражается соотношением Y
= CX,
где C
– некоторая, вообще говоря, прямоугольная
матрица
 .
.
Определение
Система называется управляемой, если существует ограниченный вектор управления G , под действием которого она переводится за конечное время из любого начального состояния X в начало координат X=(0,0,…0)T.
Если это свойство относится не ко всем компонентам вектора состояния, то система не полностью управляема. В частности, система может оказаться и полностью неуправляемой (если ни по какой координате система не обладает свойством управляемости).
Теорема Калмана.
Составим
матрицу из n
строк и nm
столбцов
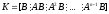 .
.
Система будет полностью управляемой, если ранг матрицы K равен n.
Пример
15.1. Пусть система описывается уравнениями
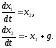
Запишем
матрицы
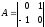 ,
,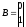 и
и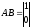 .
.
Составим
матрицу Калмана
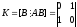 .
.
Определитель этой матрицы не равен нулю, следовательно ее ранг равен 2 и система управляема.
3.Вынужденные колебания в нелинейных системах. Условия существования.
Исследование вынужденных колебаний в нелинейных системах связано с определенными затруднениями из-за невозможности применения принципа суперпозиции, которым мы часто пользовались при исследовании линейных систем. Если на вход нелинейной системы поступает гармоническое воздействие, то на ее выходе возникает сложный многочастотный режим. Принцип гармонической линеаризации основан на отбрасывании высших гармоник. При этом рассматриваются наиболее простые одночастотные вынужденные колебания. На рис.26.1 представлена структурная схема с периодическим воздействием на входе.
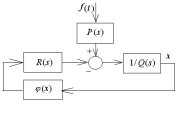 Рис.26.1.
Система с периодическим воздействием
на входе.
Рис.26.1.
Система с периодическим воздействием
на входе.
Применяя принцип гармонической линеаризации, запишем нелинейную характеристику в виде
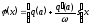 .
.
Предполагая,
что выход нелинейной системы -
гармоническая функция той же частоты,
что и входное воздействие, запишем
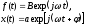 .
.
Заменив,
как обычно, в операторах, показанных на
структурной схеме s
на j,
имеем
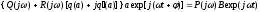 .
.
Т.к. экспоненциальная функция не обращается в нуль ни при каком значении времени t, то в результате сокращения получаем
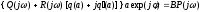 (26.1)
(26.1)
Уравнение (26.1) содержит две неизвестные величины: амплитуду a установившихся колебаний выходной координаты и ее фазу . Решение уравнения можно получить, имея в виду весьма прозрачное графическое толкование. Записав уравнение в форме
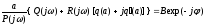 ,
(26.2)
,
(26.2)
замечаем,
что правая часть не зависит от частоты
и при изменении фазы в пределах
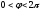 геометрически соответствует окружности
радиусаB.
Левая же часть Z(a,)
при
фиксированном значении амплитуды a
и переменной
частоте
соответствует некоторому годографу,
который может быть построен по обычным
правилам (с выделением вещественной и
мнимой частей). На рис.26.2 показаны
годограф левой части уравнения (26.1) и
окружность радиуса B
с центром в начале координат.
геометрически соответствует окружности
радиусаB.
Левая же часть Z(a,)
при
фиксированном значении амплитуды a
и переменной
частоте
соответствует некоторому годографу,
который может быть построен по обычным
правилам (с выделением вещественной и
мнимой частей). На рис.26.2 показаны
годограф левой части уравнения (26.1) и
окружность радиуса B
с центром в начале координат.
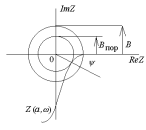 Рис.26.2.Графическое
решение уравнения (26.2)
Рис.26.2.Графическое
решение уравнения (26.2)
Из
рис.26.2 видно, что при значении амплитуды
внешнего воздействия
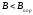 решения уравнения (26.2) не существует.
При радиусе окружности, превышающем
пороговое значения амплитуды внешнего
воздействия решение возможно в точке
пересечения годографа левой частиZ(
a
,)
с окружностью. При этом определяется
значение частоты и фазы при выбранном
значении амплитуды a
для построения годографа. Можно поступить
наоборот – построить семейство годографов
с параметром a
и набора
фиксированных значений частоты и
определить пороговую амплитуду входного
воздействия, при которой одночастотный
режим возникает на выходе нелинейной
системы. При этом можно выявить резонансные
свойства системы, а также явление так
называемого захвата
частоты. Таким
путем можно получить зависимость
порогового значения входного воздействия
от частоты (рис.26.3). С другой стороны
можно получить однопараметрическое
семейство частотных характеристик
нелинейной системы, т.е. зависимости
амплитуды выходного сигнала от частоты
для различных значений амплитуды
входного воздействия. Здесь следует
вспомнить, что в случае линейной системы
амплитудная частотная характеристика
не зависела от амплитуды входного
воздействия.
решения уравнения (26.2) не существует.
При радиусе окружности, превышающем
пороговое значения амплитуды внешнего
воздействия решение возможно в точке
пересечения годографа левой частиZ(
a
,)
с окружностью. При этом определяется
значение частоты и фазы при выбранном
значении амплитуды a
для построения годографа. Можно поступить
наоборот – построить семейство годографов
с параметром a
и набора
фиксированных значений частоты и
определить пороговую амплитуду входного
воздействия, при которой одночастотный
режим возникает на выходе нелинейной
системы. При этом можно выявить резонансные
свойства системы, а также явление так
называемого захвата
частоты. Таким
путем можно получить зависимость
порогового значения входного воздействия
от частоты (рис.26.3). С другой стороны
можно получить однопараметрическое
семейство частотных характеристик
нелинейной системы, т.е. зависимости
амплитуды выходного сигнала от частоты
для различных значений амплитуды
входного воздействия. Здесь следует
вспомнить, что в случае линейной системы
амплитудная частотная характеристика
не зависела от амплитуды входного
воздействия.
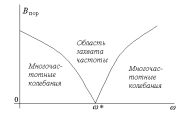 Рис.26.3.
Зависимость пороговой амплитуды от
частоты возмущающего воздействия
Рис.26.3.
Зависимость пороговой амплитуды от
частоты возмущающего воздействия
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 16
