2.Каким порядком астатизма должна обладать следящая система, чтобы при входном воздействии вида tn установившаяся ошибка была равна нулю?

3.Исследование следящей системы с нелинейным элементом типа «линейная зона с участками насыщения».

Рассмотрим следящую систему со структурной схемой, изображенной на рис.20.1. В качестве усилителя здесь используется нелинейный элемент с характеристикой 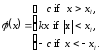(20.1)

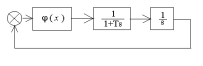
Рис.20.1. Структурная схема следящей системы с нелинейным усилителем.

Дифференциальное уравнение следящей системы 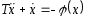. (20.2)

Введем обозначение 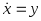. Тогда уравнение(20.2) сводится к двум уравнениям первого порядка нормальной форме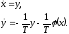(20.3)

Согласно (20.1) фазовая плоскость разбивается на три области (рис.20.2). Справа от зоны линейности система (20.3) принимает вид

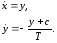
Поделив уравнения, получим одно дифференциальное уравнение

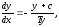
которое определяет семейство фазовых траекторий 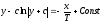. (20.4)

Семейство фазовых траекторий слева от зоны линейности получается заменой с на –с в последнем выражении.

Перейдем к построению фазового портрета в зоне линейности. Согласно (20.1) при этом уравнения (20.3) примут вид

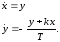
Поделив уравнения, получаем одно линейное уравнение, определяющее семейство фазовых траекторий в линейной зоне 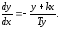(20.5)

В зависимости от коэффициента k получаются различные виды траекторий. Для качественного исследования их необходимо найти корни характеристического уравнения

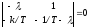. Очевидно,

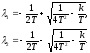
Возможны следующие случаи:

1. 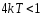- оба корня вещественны и отрицательны, устойчивый узел

2. 4kT = 1 - двукратный корень характеристического уравнения равен -1/2T – вырожденный узел

3. 4kT > 1 – корни компл. сопр. фокус

Дальнейшее повышение крутизны нелинейной характеристики не приводит к качественным изменениям фазового портрета.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 5

1.Общий вид дифференциального уравнения многомерной системы управления.

Попытаемся обобщить приемы линеаризации на случай системы с произвольным числом выходов и входов. Такие автоматические системы называются многомерными. Типичным примером многомерной системы служит система управления самолетом. Выходные координаты, которые регулируются системой управления суть следующие:

высота полета H,

направление полета,

скорость полета V,

подъемная сила Y,

лобовое сопротивление X,

крен .

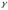Указанные координаты регулируются соответствующими входными величинами:

рулем высоты,

рулем направления,

положением сектора газа,

закрылками и предкрылками (X,Y),

элеронами.

Совокупность выходных координат обозначать вектором-столбцом

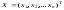
Уравнения, описывающие систему управления, запишем в нормальной форме (в форме Коши)

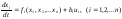(4.4)

, .

Вектор 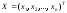называетсявектором состояния системы.

Покажем теперь, что матричная форма записи дифференциального уравнения может быть получена непосредственно из уравнения вида (1.1), которое мы использовали для вывода частотного оператора и передаточной функции. Для этого введем обозначения

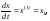
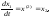(4.6)

,

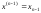Обозначения (4.6) следует рассматривать как совокупность дифференциальных уравнений.

Далее без потери общности введем для краткости обозначения для коэффициентов

.

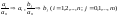Последнее уравнение, дополняющее (4.6) до системы запишется в виде

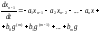. (4.7)

Уравнения (4.6) и (4.7) образуют систему, которую можно записать в матричной форме (4.5), где матрица

.

Нетрудно убедиться, что матрица

,

состоящая из строк и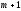столбца после умножения на вектор

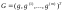образует также вектор-столбец, и вся совокупность уравнений (4.6) и (4.7) приобретает вид

,

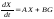который с точностью до обозначения управляющего воздействия совпадает с (4.5).