
- •1.Методы математического описания линейных систем управления.
- •2.Связь между частотными критериями устойчивости и методами выделения области устойчивости в пространстве параметров.
- •3.Аналитическое описание нелинейных элементов. Кусочно-линейная аппроксимация.
- •1.Типовые тестовые воздействия и их краткая характеристика.
- •2.Импульсная переходная характеристика линейной системы управления.
- •3.Метод фазового пространства исследования нелинейных систем.
- •1.Периодические и непериодические сигналы. Преобразование Лапласа.
- •2.Коэффициенты ошибок следящих систем.
- •3.Типы особых точек фазового пространства.
- •1.Передаточная функция линейной динамической системы. Классификация элементов.
- •2.Каким порядком астатизма должна обладать следящая система, чтобы при входном воздействии вида tn установившаяся ошибка была равна нулю?
- •3.Исследование следящей системы с нелинейным элементом типа «линейная зона с участками насыщения».
- •1.Общий вид дифференциального уравнения многомерной системы управления.
- •2.Оптимальный переходный процесс. Возможности реализации.
- •3.Исследование релейной следящей системы методом фазового пространства.
- •1.Годограф частотного оператора системы автоматического управления.
- •2. Синтез следящей системы с заданными показателями качества.
- •3.Исследование релейной следящей системы с гистерезисом.
- •1.Построить логарифмические характеристики заданного элемента.
- •2.Последовательность операций при построении характеристик корректирующих устройств.
- •3.Использование простых итераций при анализе нелинейных систем. Условия сходимости итераций.
- •1.Написать передаточную функцию по заданному графику амплитудной частотной характеристики.
- •2.Интегральная квадратическая оценка качества переходного процесса.
- •1.Построить логарифмическую частотную характеристику замкнутой следящей системы по заданному графику разомкнутой.
- •2.Интегральная оценка переходного процесса с экспоненциальным сглаживанием.
- •3. Исследование релейного автопилота. Скользящий режим.
- •1.Преобразование многоконтурных структурных схем.
- •2.Алгоритм поиска минимума интегральной оценки в пространстве параметров.
- •3.Метод гармонической линеаризации. Вычисление коэффициентов.
- •1.Записать передаточную функцию при заданной структурной схеме.
- •2.Связь между качеством переходного процесса и распределением нулей и полюсов передаточной функции.
- •3.Гармоническая линеаризация идеального реле.
- •1.Определение устойчивости движения по а.М. Ляпунову.
- •2.Способы модуляции в дискретных системах управления.
- •3.Аналитическое исследование автоколебаний при гармонической линеаризации.
- •1.Теорема а.М. Ляпунова об устойчивости для систем, допускающих линеаризацию.
- •2.Рекуррентные соотношения в дискретных системах управления.
- •3.Частотный подход к анализу автоколебаний.
- •1.Практическое применение критерия устойчивости Гурвица (не ниже 4-го порядка)..
- •2.Модификация критерия Гурвица для дискретных систем.
- •1.Доказать критерий устойчивости а.В. Михайлова.
- •2.Управляемость динамических систем. Теорема Калмана об управляемости.
- •3.Вынужденные колебания в нелинейных системах. Условия существования.
- •1.Доказать критерий устойчивости Найквиста.
- •2.Наблюдаемость динамических систем. Теорема Калмана о наблюдаемости.
- •3.Вынужденные колебания в нелинейных системах. Пороговая амплитуда возбуждающего сигнала. Вибрационное сглаживание разрывных характеристик.
- •2.Какое влияние оказывает элемент с запаздыванием на характеристики системы управления?
- •3.Качественный анализ переходных процессов в нелинейных системах, описываемых уравнениями высокого порядка.
- •1.В чем состоит основной принцип выделения границ области устойчивости в пространстве параметров?
- •2.Изложить аналитический подход к исследованию многомерной системы управления. Распространение понятия свертки на многомерные системы.
- •3.Выделение зон затухания и возрастания амплитуды автоколебаний нелинейных систем до установившегося значения.
- •1.Выделение области устойчивости в пространстве двух параметров. Особые прямые. Правила штриховки границы.
- •2.Сформулировать условия устойчивости линейной системы управления с медленно меняющимися параметрами.
- •3.Знакоопределенные и знакопостоянные функции. Связь с устойчивостью нелинейных систем.
- •1.Теорема а.М. Ляпунова об устойчивости в общем случае (с использованием знакоопределенных функций).
- •2.Анализ устойчивости релейной следящей системы с помощью функций а.М. Ляпунова.
- •3.Анализ устойчивости автопилота с нелинейным исполнительным элементом. Абсолютная устойчивость.
- •1.Общие приемы исследования нелинейных систем произвольного порядка.
- •2.Теоремы а.М. Ляпунова об асимптотической устойчивости и о неустойчивости.
- •1.Примеры элементов с нелинейными характеристиками.
- •2.Псевдолинейная коррекция частотных характеристик.
- •3.Преобразоание уравнения высокого порядка, описывающего линейную систему управления к нормальной системе в форме Коши.
3.Аналитическое исследование автоколебаний при гармонической линеаризации.
В
результате гармонической линеаризации
нами был получен аналог передаточной
функции нелинейного элемента в виде
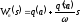 .
.
Если
передаточная функция линейной части
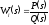 является дробно-рациональной функцией
переменнойs,то
передаточная функция контура (рис.23.1
из предыдущей лекции) в разомкнутом
виде запишется как произведение
является дробно-рациональной функцией
переменнойs,то
передаточная функция контура (рис.23.1
из предыдущей лекции) в разомкнутом
виде запишется как произведение
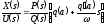 .
.
Соответственно
дифференциальное уравнение замкнутого
контура, описывающее собственное
движение системы имеет вид
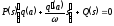 .
(24.1)
.
(24.1)
Последнее
уравнение можно рассматривать как
характеристическое относительно
переменной s.
При наличии автоколебаний с основной
частотой
по крайней мере одна пара корней
характеристического уравнения будет
мнимой, т.е. вместо (24.1) следует записать
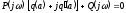 .
(24.2)
.
(24.2)
Выделив
мнимую и вещественную части, получаем
систему из двух уравнений
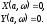 (24.3)
(24.3)
Решив
ее относительно частоты и амплитуды,
получаем искомые параметры автоколебаний.
Решение задачи становится особенно
простым в случае однозначной нечетной
нелинейной характеристики, когда, как
мы знаем,
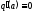 .
В этом случае уравнение (24.2) приобретает
вид
.
В этом случае уравнение (24.2) приобретает
вид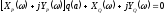 .
.
Отсюда
следует
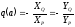 .(24.4)
.(24.4)
Мы
получаем отдельное уравнение для
определения частоты
 .
.
Если существует вещественный корень, то, подставив его в (24.4), мы получаем соотношение для определения амплитуды.
Таким
образом, формально процедура определения
параметров автоколебаний не вызывает
затруднений. Остается невыясненным
вопрос о физической
реальности
найденных параметров. Для выяснения
этого вопроса дадим приращение амплитуде
и частоте предполагаемых автоколебаний
и исследуем поведение этих приращений
(вариаций) по времени. Запишем
неустановившийся режим в комплексной
форме:
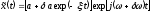 . (24.5)
. (24.5)
Раскрыв
левую квадратную скобку, имеем
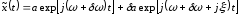 .
Обратимся теперь к уравнению, вытекающему
из (24.2),
.
Обратимся теперь к уравнению, вытекающему
из (24.2), .
.
Запишем
разложение в окрестности точки
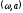 ,
ограничиваясь линейными членами,
,
ограничиваясь линейными членами,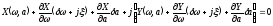 .
.
Имея
в виду (24.3), получаем систему относительно
приращений
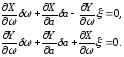
Определитель
этой системы
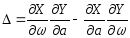 . (24.6)
. (24.6)
Устойчивость
автоколебаний зависит от поведения
приращения амплитуды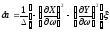 .
(24.7)
.
(24.7)
Из
(24.7) видно, что автоколебания будут
устойчивыми, если
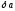 и
одного знака. Действительно, если
приращение амплитуды будет положительным,
то фазовая траектория окажется с наружной
стороны предельного цикла и для
устойчивости необходимо, чтобы приращение
убывало с течением времени. Согласно
(24.5) приращение будет убывать при
>0Аналогичное
рассуждение можно провести для случая
отрицательного приращения амплитуды,
при котором фазовая траектория оказывается
внутри предельного цикла.
и
одного знака. Действительно, если
приращение амплитуды будет положительным,
то фазовая траектория окажется с наружной
стороны предельного цикла и для
устойчивости необходимо, чтобы приращение
убывало с течением времени. Согласно
(24.5) приращение будет убывать при
>0Аналогичное
рассуждение можно провести для случая
отрицательного приращения амплитуды,
при котором фазовая траектория оказывается
внутри предельного цикла.
В
обоих случаях условием устойчивости
предельного цикла будет, как это видно
из (24.7),
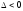 .
.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 13
1.Теорема а.М. Ляпунова об устойчивости для систем, допускающих линеаризацию.
Для
того, чтобы уравнение вида
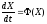 обладало устойчивым тривиальным
решением, необходимо и достаточно, чтобы
корни характеристического уравнения
обладало устойчивым тривиальным
решением, необходимо и достаточно, чтобы
корни характеристического уравнения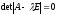 имели отрицательные вещественные части.
имели отрицательные вещественные части.
В
такой формулировке доказательство
теоремы кажется очевидным. Для этого
достаточно записать решение уравнения
(7.2) в общем виде
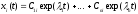 ,
(i=1,2,…n).
,
(i=1,2,…n).
