1.7. Вывод матрицы перехода от I-й к (I–1)-й системе координат
При совершении преобразования (а) по алгоритму Денавита-Хартен- берга система Pi-1xi-1yi-1zi-1 поворачивается на угол i вокруг оси zi-1 и переходит в систему Pi-1x'y'z' (рис. 1.13).
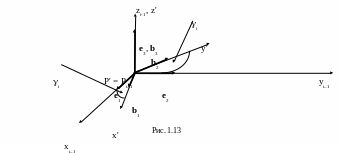
Рис. 1.13
Эти системы связываются с помощью некоторой матрицы T':
=
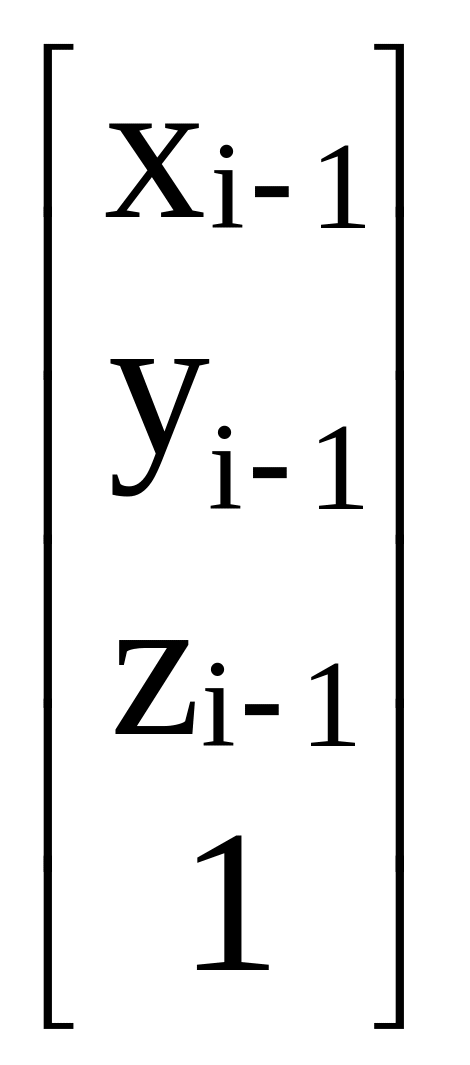T'
.
(1.26)
Для вычисления элементов матрицы T' воспользуемся формулой (1.23):
сos (b1, e1) = cos (360 – i) = cos i,
cos (b2, e1) = cos (270 – i) = – sin i,
cos (b3, e1) = cos 90 = 0,
cos (b1, e2) = cos (90 – i) = sin i,
cos (b2, e2) = cos (360 – i) = cos i,
cos (b3, e2) = 0,
cos (b1, e3) = 0,
cos (b2, e3) = 0,
cos (b3, e3) = 1,
=
0,
=
0,
=
0.
Получаем
T'
=
.
(1.27)
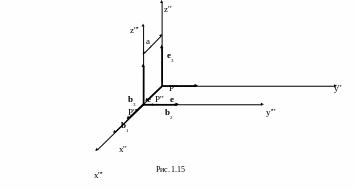
При совершении второго преобразования система P'x'y'z' смещается вдоль оси Pi–1zi–1 (или, что одно и то же, вдоль оси P'z') на величину si и переходит в систему P''x''y''z'' (рис. 1.14).
Для вычисления T'' и последующих матриц T''' и T'''' вновь пользуемся формулой (1.23):
=
.
(1.28)
При совершении третьего преобразования система P''x''y''z'' смещается вдоль оси P''x'' (или, что одно и то же, вдоль оси Pixi) на величину ai и переходит в систему P'''x'''y'''z''' (рис. 1.15).
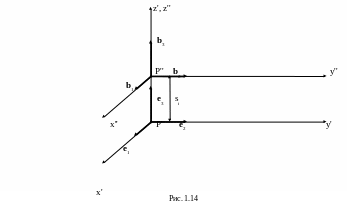
Получаем
=
.
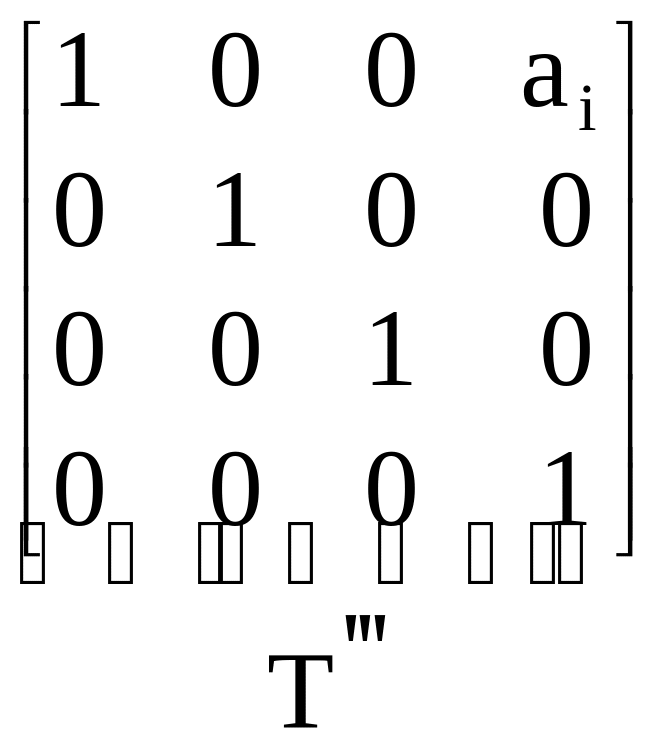
(1.29)
П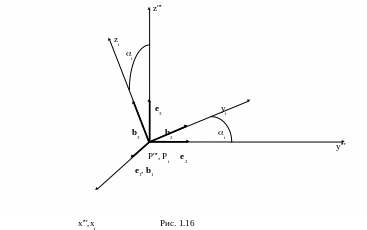
ри
совершении четвертого преобразования
система P'''x'''y'''z''' поворачивается на
угол i
вокруг оси P'''x''' (или, что одно и то же,
вокруг оси Pixi)
и переходит в систему Pixiyizi
(рис. 1.16).
Получаем
=
.
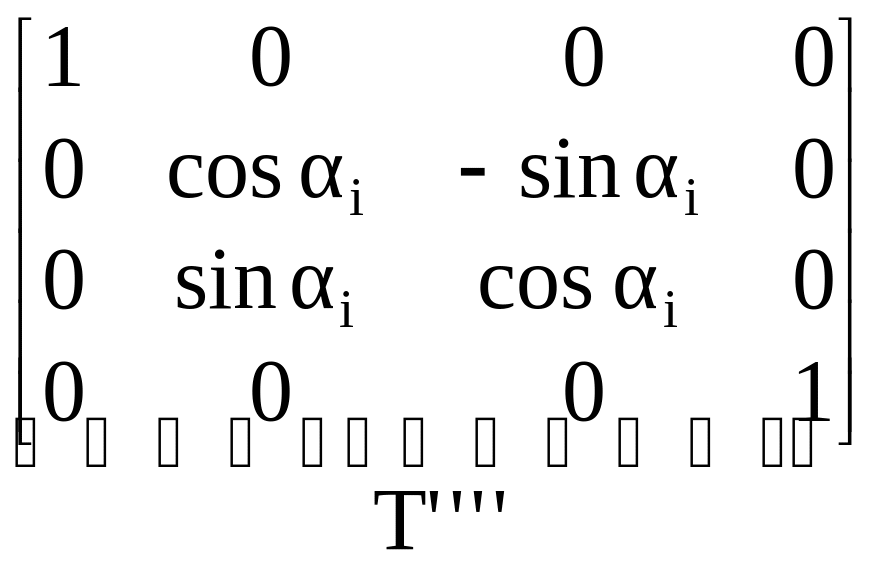
(1.30)
Поскольку
=
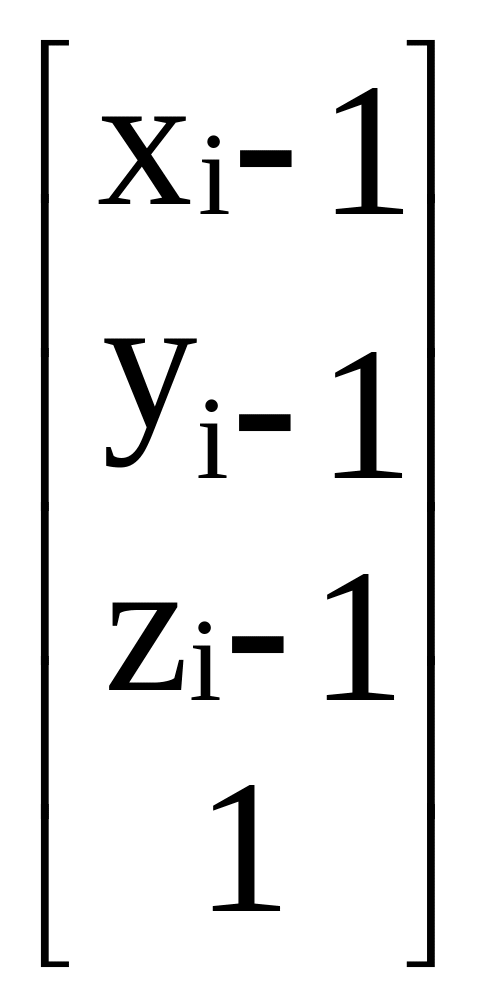T'
T''
T'''
T''''
,
(1.31)
то
=
.
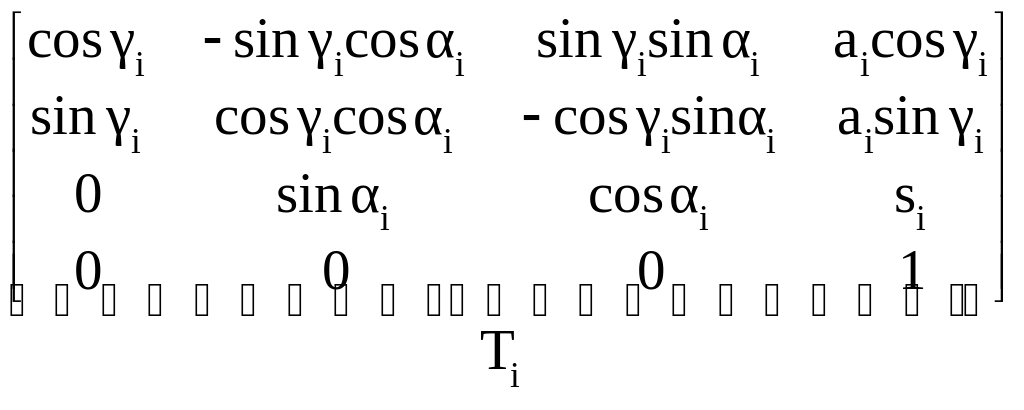
(1.32)
Матрица Ti есть матрица перехода от i-й к (i–1)-й системе координат. Напомним, что если сочленение, связывающее (i–1)-е и i-е звенья, – вращательное, то обобщенной координатой является i, если сочленение поступательное, то обобщенной координатой является si .
1.8. Уравнение кинематики манипулятора
Выведем уравнение кинематики манипулятора. Из формулы (1.32) можно видеть, что
=
T1
.
(1.33)
По той же формуле
=
T2
.
(1.34)
Тогда в общем случае получаем
=
T1
T2
...
Ti
,
(1.35)
или в векторной форме
r0A = T1(q1(t)) T2(q2(t)) ... Ti(qi(t)) riA = Si(q1(t), q2(t),..., qi(t)) riA. (1.36)
Формула (1.36) и есть уравнение кинематики манипулятора. Она позволяет вычислить координаты любой точки (а следовательно, и всех точек) манипулятора в базовой системе координат, если известны координаты этой точки в i-й системе и известно, как изменяются обобщенные координаты. Таким образом мы можем получить полную информацию о характере движения манипулятора.
Кинематика человекоподобного робота. Во введении мы говорили о том, что механика манипулятора, т. е. искусственной «руки», не отличается принципиально от механики человекоподобного робота. Мы рассматривали манипулятор как совокупность твердых тел, связанных друг с другом, но способных двигаться друг относительно друга.
Человекоподобного робота, так же, как и механическую руку, можно рассматривать как совокупность твердых тел, связанных друг с другом, но способных двигаться друг относительно друга.
Связав свою систему координат с каждым звеном робота (рис. 1.18) и учтя связи в сочленениях, можно, как и в случае с манипулятором, получить формулы, описывающие движение каждой точки робота в базовой системе координат.
После этого можно будет вычислить силы, которые надо будет приложить к звеньям человекоподобного робота, а затем подать эти силы через двигатели.
Подробно описание механики человекоподобных роботов можно найти в литературе [1].