3.7. Управление манипуляторами в среде с неизвестными препятствиями

Вопрос планирования пути манипулятора в среде с известными препятствиями уже рассмотрен. Следует отметить, что задача составления списка запрещенных конфигураций является очень трудоемкой. На практике может возникнуть необходимость перемещения манипулятора в среде, заполненной препятствиями очень сложной формы. Причем может оказаться так, что перед началом движения у манипулятора вообще не будет информации о наличии в рабочей области препятствий, их количестве и форме. Поэтому возникает задача разработки алгоритмов управления роботами в среде с неизвестными препятствиями.

Некоторые алгоритмы планирования движения в известной среде в принципе могут быть использованы и для неизвестной среды. Если дискретизироватъ пространство состояний, то можно использовать графовые методы поиска траектории движения динамических систем (ДС) из q⁰ в q^T [9, 16]. Однако эти алгоритмы имеют одно общее свойствo, которое затрудняет их применение для управления ДС в неизвестной среде: они в том или ином объеме требуют осуществлять поиск в ширину, иначе не гарантируется достижение целевой точки [5]. Но при поиске в ширину часто возникает следующая ситуация: предположим, что мы только что закончили рассмотрение вершин, соседних вершине q, и теперь нам надо рассматривать вершины, соседние вершине q', и вершины q и q' не являются соседними. Для того, чтобы рассмотреть вершины, соседние q', ДС должна сначала передвинуться в q'. Таким образом, возникает задача планирования маршрута из q в q', другими словами, мы получаем первоначальную задачу планирования траектории, в которой только q⁰ и q^Т заменены на q и q'. При планировании же в известной среде ЭВМ просто «переключает свое внимание» от q к q', которые хранятся в памяти ЭВМ. Необходимость поиска и реализации путей для многих различных q и q⁰' делает общую сумму передвижений ДС очень большой. В соответствии с классификацией [16] представителями алгоритмов поиска в ширину являются собственно алгоритм поиска в ширину, эвристический поиск «первый - лучший», ленивый вероятностный маршрут, динамическое программирование. В методах, основанных на случайном потенциальном поле, алгоритме «Нить Ариадны», быстроисследующих случайных деревьях [16] новые вершины генерируются случайным образом, и потому они имеют вышеописанный недостаток, вызывающий множество перемещений в новые случайно сгенерированные вершины.

Известно также, что алгоритмы поиска в глубину не всегда доводят до цели [5].

Для решения нашей задачи может быть использован подход, основанный на автоматическом доказательстве теорем [10], но этот подход требует рассмотрения большого числа вариантов и направлений поиска и поэтому его применение оказывается неэффективным [3].

В методе искусственных потенциалов [12] ДС представляется в виде заряженной точки, запрещенные состояния наделяются отталкивающими потенциалами, целевая точка - притягивающим потенциалом. Работа метода демонстрируется для известных запрещенных состояний. Не указывается, как распоряжаться поступающей информацией об обнаружении ранее неизвестных запрещенных состояний. В общем случае нет гарантии того, что траектория, свободная от столкновений, будет найдена [11].

Для методов планирования траектории в среде с наперед известными запрещенными состояниями имеется одна общая трудность: очень трудно собрать заранее полную информацию о расположении запрещенных состояний в рабочей зоне ДС и представить эту информацию в виде, пригодном для учета при планировании траектории. В случае нашего алгоритма можно будет видеть, что собирать полную информацию о запрещенных состояниях заранее не требуется, ДС будет собирать необходимую информацию самостоятельно в ограниченных объемах и в терминах пространства состояний, что удобно для планирования траектории.

В [18] представлен алгоритм управления классом ДС - роботами-манипуляторами среди неизвестных препятствий, расположенных в трехмерном декартовом пространстве. Манипулятор должен иметь не более трех звеньев и последняя кинематическая пара должна быть поступательной. При вышеуказанных предварительных условиях алгоритм гарантирует достижение цели за конечное число шагов.

В [1, 6] описано применение семантических сетей (или М-сетей) для задачи управления роботами в неизвестной среде. Недостатком такого подхода является необходимость предварительного обучения сети, которая моделирует работу планирующей системы. Отсутствие формальных алгоритмов обучения делает невозможным обучение сложной сети, которая должна планировать действия робота в среде, близкой к естественной.

В [2, 8] предлагается преобразовать подход, основанный на пространстве конфигураций, с тем, чтобы иметь возможность описывать движение робота в неизвестной среде. Для этого результатам действий робота и ситуациям в среде предлагается приписывать оценки доверия, основанные на формализмах теории вероятностей, модальной или нечеткой логики. Но метода для генерации обоснованных оценок не предложено. В [3] предлагается ввести в систему логического вывода оценки правдоподобности вывода, соответствующие неопределенности ситуаций в среде, но не говорится о том, как назначать эти оценки.

Опишем наш алгоритм движения манипуляторов в среде с неизвестными препятствиями. Алгоритм применяется для манипуляторов с произвольным конечным числом звеньев, функционирующих в среде с препятствиями, расположение, количество и форма которых произвольны. Будет доказано, что, двигаясь по этому алгоритму, манипулятор достигнет цели за конечное число шагов при условии достижимости цели. Описание нижеприведенного метода позволяет увидеть, что манипулятор составляет список известных запрещенных конфигураций сам. Планирование пути осуществляется в пространстве обобщенных координат.

Сформулируем задачу движения манипулятора в среде с неизвестными препятствиями: даны начальная конфигурация q⁰ и целевая конфигурация q^T, в рабочей области могут располагаться препятствия, но перед началом движения информация о наличии препятствий, их количестве, расположении и форме отсутствует. Требуется сделать так, чтобы манипулятор передвинулся из q⁰ в q^T.

Примем следующие допущения:

1) положение, форма и размеры препятствий неизменны в течение всего времени движения манипулятора (препятствия стационарны);

2) заранее известно, что цель достижима (т. е. известно, что в пространстве обобщенных координат можно найти линию, соединяющую q⁰ и q^T и не налегающую ни на одно присутствующее в рабочей зоне препятствие);

3) обобщенные координаты должны удовлетворять ограничениям (3.1);

4) манипулятор снабжен сенсорной системой, позволяющей определять, налегает или не налегает манипулятор на препятствия в каждой из конфигураций, лежащих в небольшой r-окрестности текущей конфигурации (в том числе - налегает ли на препятствия текущая конфигурация). Под r-окрестностью будем понимать гипершар радиуса r в пространстве конфигураций (круг в двумерном случае, шар в трехмерном случае, гипершар в n-мерном случае) с центром в текущей конфигурации. Устройство сенсорной системы рассматривать не будем;

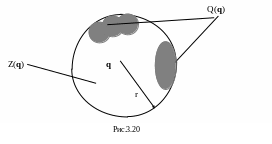
5) если, по крайней мере, одна точка манипулятора, находящегося в некоторой конфигурации q, принадлежит внутренней области хотя бы одного препятствия, либо данная конфигурация q не удовлетворяет ограничениям (3.1), то будем считать такую конфигурацию манипулятора запрещенной. В остальных случаях конфигурация считается разрешенной. Множество всех конфигураций из r-окрестности некоторой конфигурации q обозначим как Y(q). Множество всех запрещенных конфигураций из Y(q) обозначим как Q(q), множество всех разрешенных конфигураций из Y(q) обозначим как Z(q). Множества Y(q), Q(q) и Z(q) могут выглядеть в виде списков либо записываться с помощью формул либо другим способом.

Главное, что мы считаем, что у нас есть способ записи всех конфигураций во множества Y(q), Q(q) и Z(q). Примерный вид r-окрестности некоторой точки q с обнаруженными в ней множествами Z(q) и Q(q) показан на рис. 3.20.

Обращаем внимание, что множества Z(q) и Q(q) могут быть не непрерывными.

Приведем алгоритм управления манипуляторами в среде с неизвестными препятствиями.

1. Находясь в q⁰, манипулятор исследует r-окрестность q⁰ и формирует множества Z(q⁰) и Q(q⁰). Затем манипулятор планирует в пространстве конфигураций траекторию q(t). Траектория должна удовлетворять следующим условиям:

– соединять q⁰ и q^Т;

– не налегать ни одной своей точкой ни на одну из точек из Q(q⁰);

– удовлетворять конструктивным ограничениям (3.1).

Манипулятор начинает двигаться по этой траектории.

2. При отработке этой траектории возможны два исхода:

2.1) манипулятор не встретит на своем пути препятствий и, как следствие, достигнет целевой конфигурации q^T, по достижении q^T алгоритм заканчивает свою работу;

2.2) манипулятор придет в точку (обозначим ее через qⁿ, n = 1,2,…), следующая за которой налегает на препятствия.

В этом случае манипулятор, находясь в qⁿ, исследует r-окрестность около qⁿ и формирует множества Z(qⁿ) и Q(qⁿ). Затем манипулятор планирует траекторию, которая должна удовлетворять следующим условиям:

– соединять qⁿ и q^T;

– не налегать на множества Q(qⁱ), i=0, 1, ... , n;

– удовлетворять ограничениям (3.1).

Манипулятор начинает двигаться по этой траектории, n увеличивается на 1, а алгоритм переходит на п. 2.

Теорема. Если манипулятор будет двигаться по вышеприведенному алгоритму, то он достигнет цели за конечное число шагов.

Доказательство. Пусть манипулятор, находясь в qⁿ, спланировал траекторию, приводящую его в q^T, и начал по этой траектории двигаться. Если во время движения манипулятор не встретит препятствий, он достигнет цели за конечное число шагов (в силу конечности длины траектории). Поэтому бесконечность блуждания манипулятора может быть вызвана только бесконечной сменой предварительной траектории.

Бесконечность смены предварительной траектории может быть вызвана следующими обстоятельствами:

– манипулятор будет все время попадать в одну и ту же точку смены траектории;

– число точек смены траектории будет бесконечным.

Покажем, что все точки смены траектории различны. Предположим, что манипулятор сменил траекторию, находясь в точке q^s, а потом опять сменил траекторию, будучи в точке q^p, т. е. s < p. Покажем, что q^s  q^p. Предположим сначала, что q^s = q^p. Тогда Q(q^s) = Q(q^p). Находясь в q^s, манипулятор сгенерировал траекторию, не налегающий на множества Q(qⁱ), i = 0, 1, ..., s. Затем манипулятор, оказавшись в q^p, обнаружил, что эта точка является запрещенной, т. е. обнаружил, что предварительная траектория налегает на Q(q^p) = Q(q^s), что невозможно. Получили противоречие. Следовательно, все точки смены траектории различны.

Покажем, что число точек смены траектории конечно. Предположим, что, наоборот, оно бесконечно. Все точки смены траектории должны удовлетворять ограничениям (3.1). Это означает, что последовательность этих точек ограничена. Согласно теореме Больцано-Вейерштрасса, из этой последовательности можно извлечь сходящуюся подпоследовательность qⁱ, i = 1, 2, … В соответствии со свойством Коши сходящихся последовательностей для любого  можно найти такой номер s, что все точки qⁱ, i > s, будут лежать в -окрестности точки q^s. Возьмем <r. Рассмотрим произвольную точку смены траектории qⁱ, расположенную в -окрестности точки q^s. Так как манипулятор, находясь в qⁱ, сменил свою траекторию, то это означает, что последняя налегала на множество Q(q^s), потому что qⁱ и ее соседние точки принадлежат Q(q^s). Отсюда можно сделать вывод: множество Q(q^s) не было учтено при генерации той траектории, что невозможно при строгом выполнении предписаний алгоритма. Таким образом, если принять, что число точек смены маршрута бесконечно, то неизбежно возникнет ситуация, которая не может наступить при строгом следовании предписаний алгоритма. Следовательно, число точек смены маршрута конечно. Теорема доказана.

Итак, число случаев, когда манипулятору придется строить новую траекторию из текущей конфигурации в целевую, будет конечным. Каждый раз, когда манипулятору надо будет решать задачу генерации новой траектории, ему, фактически, надо будет решать задачу ПИ планирования траектории в среде с известными препятствиями (спланировать траекторию из текущей точки в целевую, такую, чтобы она не налегала на уже известные запрещенные точки). Методы планирования путей и траекторий в среде с известными запрещёнными состояниями рассмотрены в настоящем учебном пособии, а также в [16, 18]. Итак, задача управления манипуляторами в среде с неизвестными препятствиями сводится к решению конечного числа задач планирования траекторий манипулятора в среде с известными препятствиями.