
- •П. К. Лопатин Интеллектуальные манипуляционные роботы
- •Предисловие
- •Введение
- •1. Кинематика манипуляторов
- •1.1. Манипулятор как система твердых тел
- •1.2. Кинематика произвольного движения тела,
- •1.3. Кинематика поступательного движения тела
- •1.4. Кинематика произвольного движения твердого тела
- •1.5. Характер связей между звеньями
- •1.6. Расстановка систем координат по алгоритму Денавита-Хартенберга
- •1.7. Вывод матрицы перехода от I-й к (I–1)-й системе координат
- •1.8. Уравнение кинематики манипулятора
- •1.9. Скорость и ускорение некоторой точки манипулятора
- •Правая часть (1.45), если k j, k I;
- •0, Если k j.
- •1.10. Прямая задача кинематики
- •1.11. Обратная задача кинематики
- •Примеры решения задач
- •Разделим уравнение (1.71) на (1.72). Получим
- •Задачи для самостоятельного решения
- •Библиографический список
- •2.1. Уравнения Лагранжа II рода
- •2.2. Кинетическая энергия манипулятора
- •Поскольку интеграл – это сумма, то формулу (2.3) можно записать в виде уравнения
- •Из (1.36) следует, что
- •Из формулы (1.42) видно, что
- •2.3. Потенциальная энергия манипулятора
- •2.4. Уравнение динамики манипулятора
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3. Планирование путей, траекторий и управление манипуляторами
- •3.1. Понятие пространства обобщенных координат.
- •Постановки задачи
- •3.2. Планирование пути методом полиномиальной аппроксимации
- •Решая эту систему, получим
- •3.3. Планирование пути с учетом ограничений на положение, скорость и ускорение
- •3.4. Планирование траектории с учетом динамики манипулятора
- •Библиографический список
- •3.5. Исполнение траектории
- •Библиографический список
- •Библиографический список
- •3.6.1. Алгоритм полного перебора
- •Библиографический список
- •3.6.2. Алгоритм перебора в глубину
- •3.6.3. Алгоритм а*
- •Библиографический список
- •3.6.4. Алгоритм фронта волны
- •Библиографический список
- •3.6.5. Алгоритм полиномиальной апроксимации
- •Библиографический список
- •3.6.6. Диаграммы вороного
- •Библиографический список
- •3.6.7. Алгоритм разделения ячеек
- •1. Предварительный поиск маршрута
- •2. Разделение плоскости на свободные области
- •3. Соединение свободных областей
- •4. Объединение свободных соединенных областей
- •5. Соединение свободных областей на соседних плоскостях
- •6. Создание объединенных областей и проверка достижимости
- •7. Построение маршрута
- •8. Пример
- •Библиографический список
- •Примеры решения задач
- •3.7. Управление манипуляторами в среде с неизвестными препятствиями
- •Библиографический список
- •Алгоритм
- •3.8. Иерархия уровней Управления роботами
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Заключение
- •Учебное издание
- •Учебное пособие
Примеры решения задач
Задача 1. Вычислите матрицы инерции Hi (i=1, 2, 3) звеньев манипулятора (рис. 1.20).
Решение. Для составления уравнений движения манипулятора в форме уравнений Лагранжа II рода необходимо знать матрицы инерции звеньев Hi, (i=1,2,3), определенных по формуле (2.14).
Интегралы в (2.14) берут по объему U звена i (i = 1, 2, 3). Они являются тройными интегралами, которые более детально записывают в виде
![]() ,
(2.51)
,
(2.51)
где dv – элемент объема. Вычисление интеграла (2.51) сводится к последовательному вычислению трех определенных интегралов по каждой из переменных x, y, z. Пределы интегрирования расставляются в зависимости от формы области U.
Звенья манипулятора будем рассматривать как однородные сплошные или тонкостенные полые цилиндры (рис. 2.2).
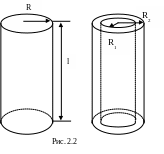
Найдем матрицу инерции для первого звена, считая его цилиндром с радиусом R1 и высотой l1 (длина звена).
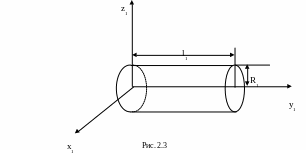
Матрица инерции зависит от выбора системы координат. Первое звено расположено относительно системы координат P1x1y1z1 так, как указано на рис. 2.3 (сравните с рис. 1.21). Тогда областью U1 является внутренность цилиндра.
Вычислим все интегралы, составляющие матрицу (2.14), для случая i = 1. В силу предположения однородности материала звеньев имеем
dm1=dv,
где – плотность материала, dv – элемент объема.
Вычислим все элементы первой строки матрицы H1:
![]()
![]() =
=
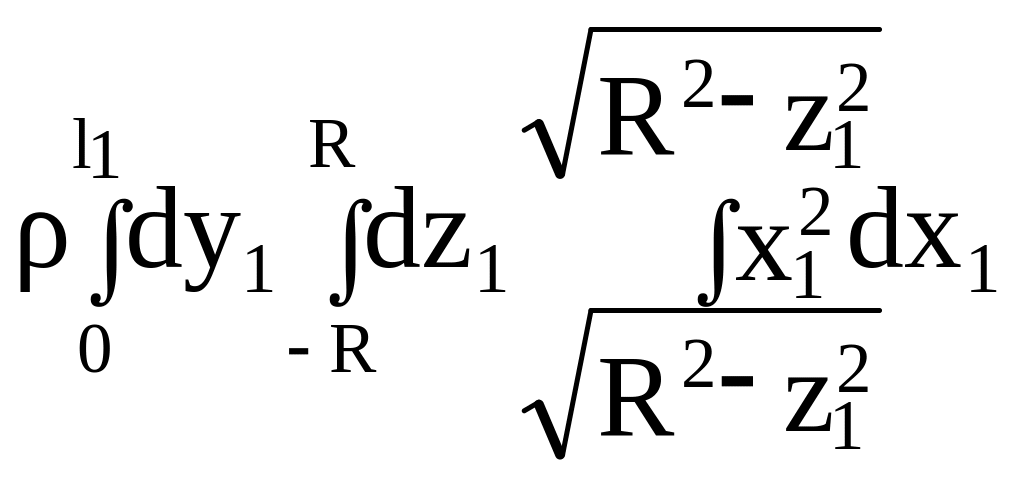 .
(2.52)
.
(2.52)
П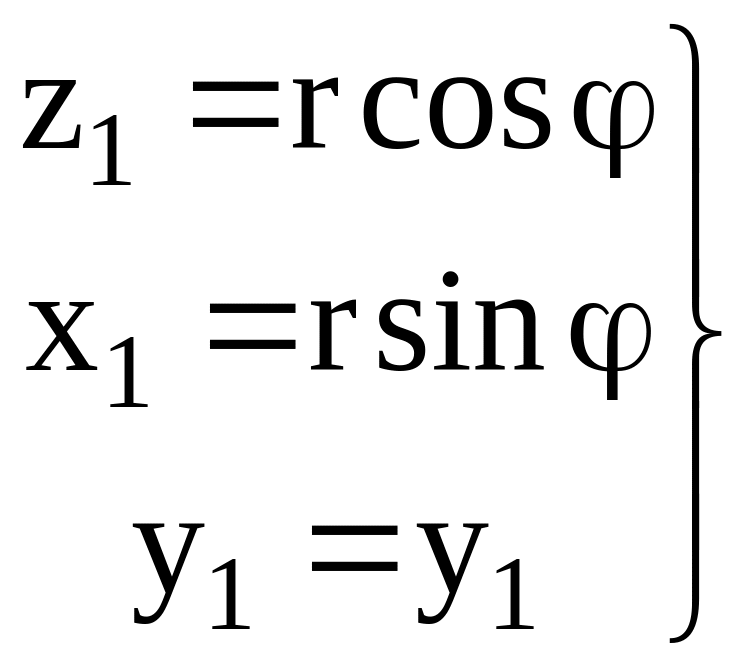 ри
введении цилиндрических координат r,
,
y1
по системе уравнений
ри
введении цилиндрических координат r,
,
y1
по системе уравнений
(2.53)
получаем
![]() =
=
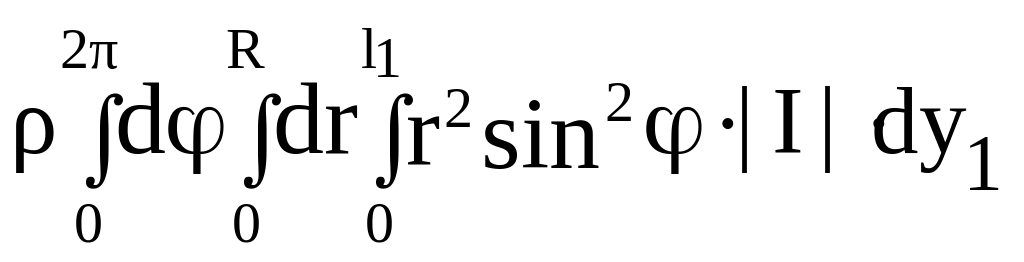 ,
(2.54)
,
(2.54)
где x взято в соответствии с (2.53) и I – якобиан преобразования переменных, который для цилиндрических координат равен r.
Итак, имеем
![]() =
=
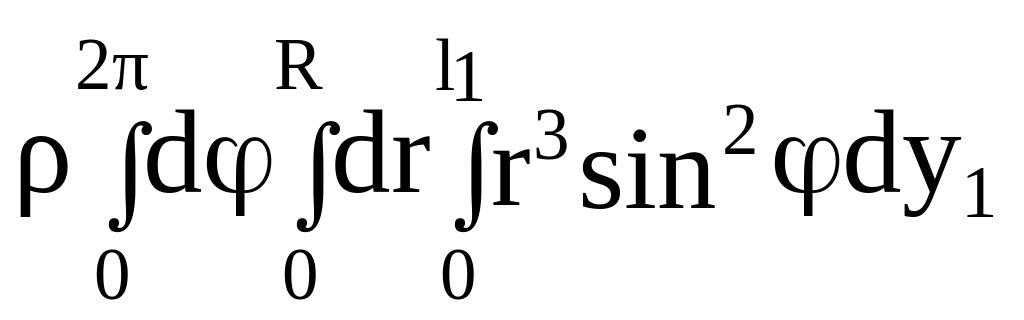 =
=
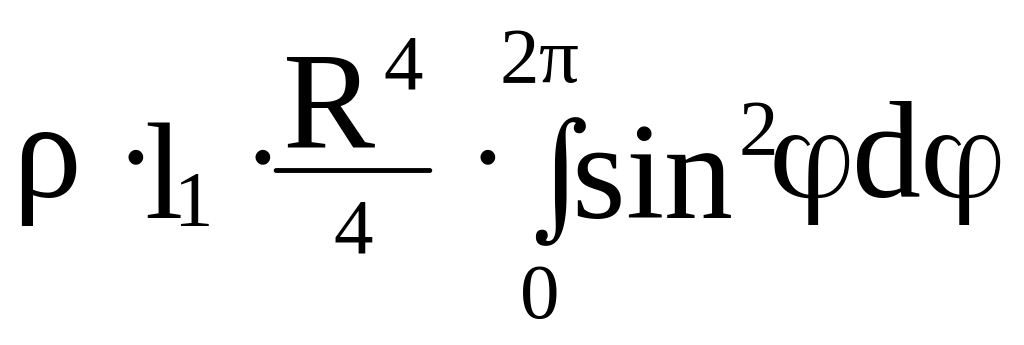 =
=
=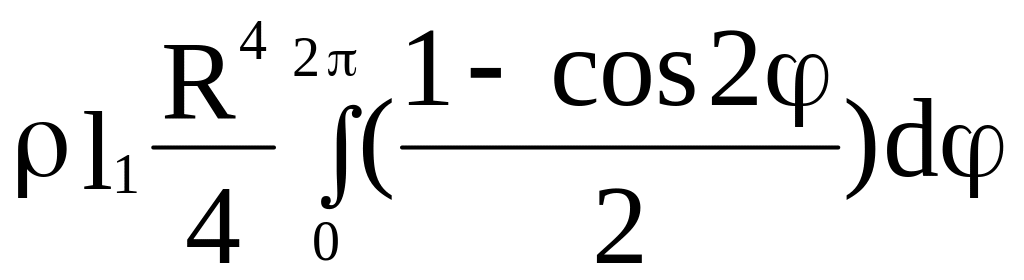 =
=
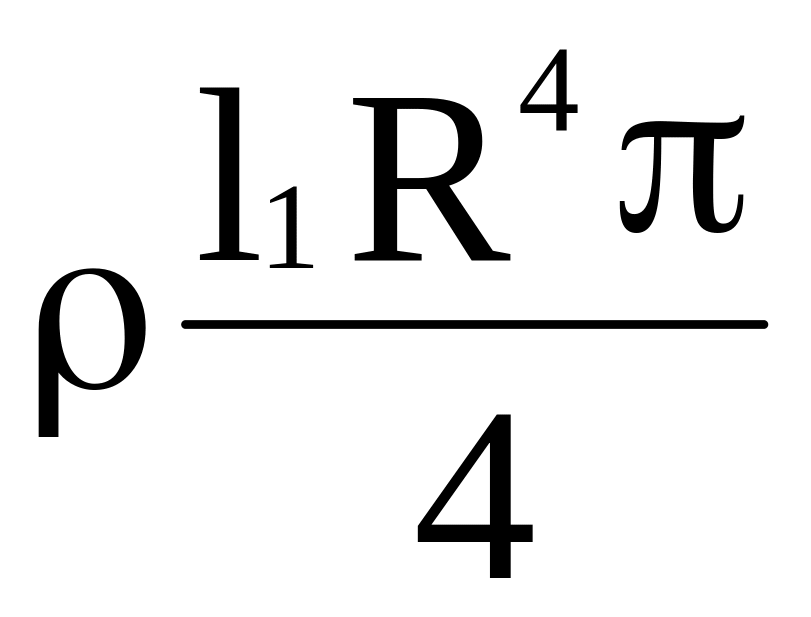 .
(2.55)
.
(2.55)
При
вычислении интеграла
![]() область интегрирования остается той
же самой, меняется подынтегральная
функция.
область интегрирования остается той
же самой, меняется подынтегральная
функция.
Вместо y1 и z1 подставляются их выражения из (2.53):
![]() =
=
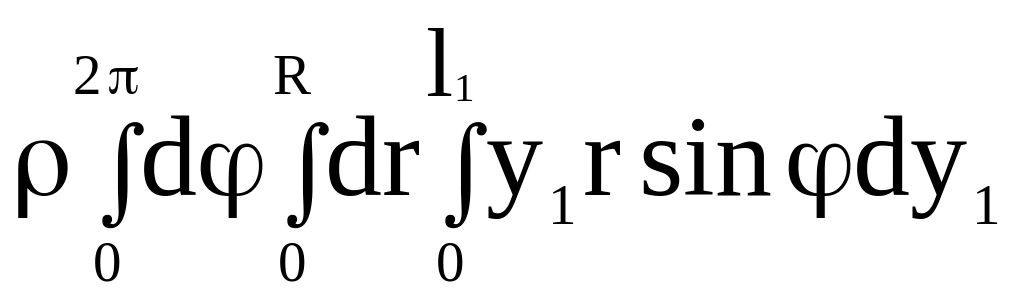 =
0. (2.56)
=
0. (2.56)
Аналогично подсчитывается следующий интеграл:
![]() =
=
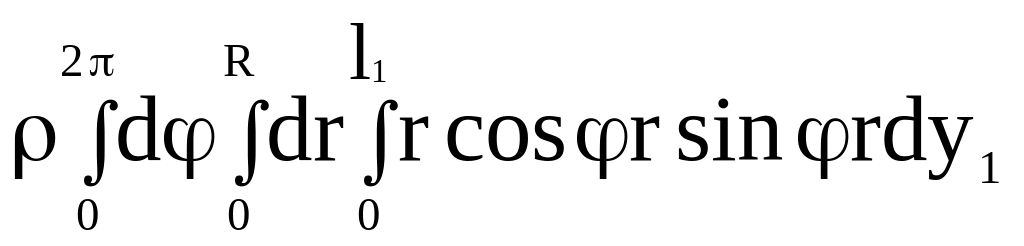 =
0. (2.57)
=
0. (2.57)
Вычислим
интеграл
![]() .
Аналогично формуле (2.55) имеем
.
Аналогично формуле (2.55) имеем
![]() =
=
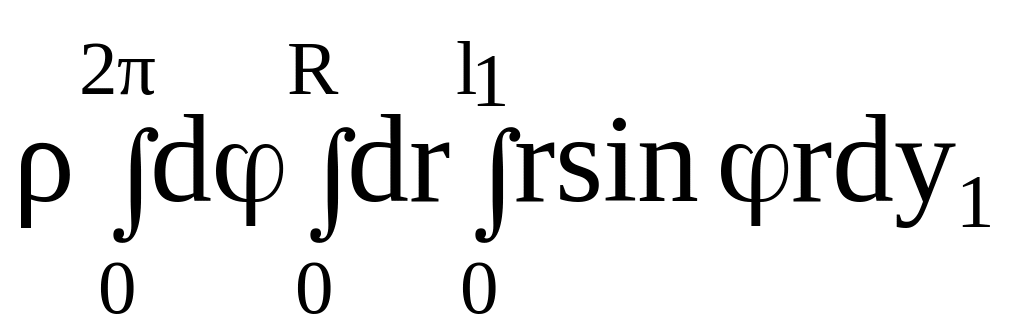 =
0. (2.58)
=
0. (2.58)
При
вычислении элементов второй строки
матрицы H1
получаем
![]() =
0 (в соответствии с (2.56)):
=
0 (в соответствии с (2.56)):
![]() =
=
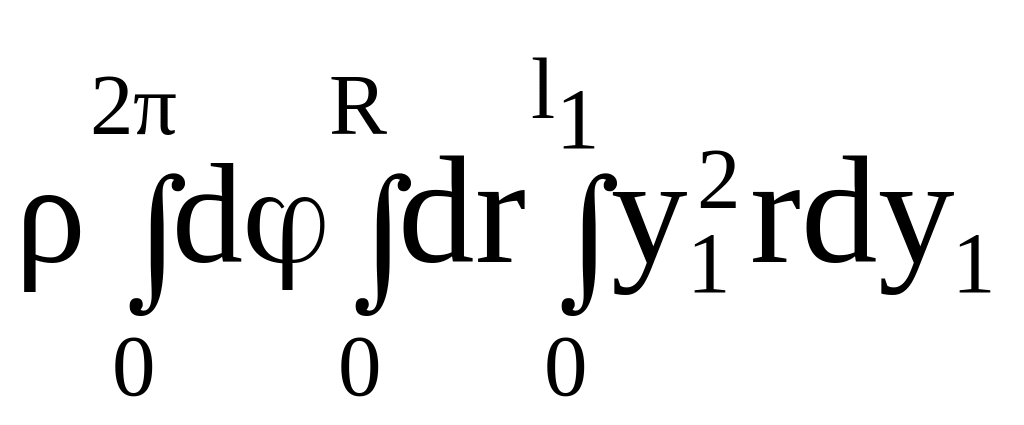 =
=
![]() =
=![]() ,
(2.59)
,
(2.59)
![]() =
=
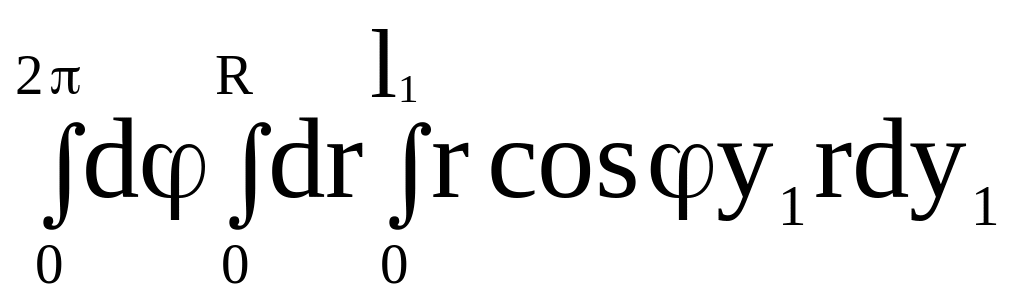 =
0, (2.60)
=
0, (2.60)
![]() =
=
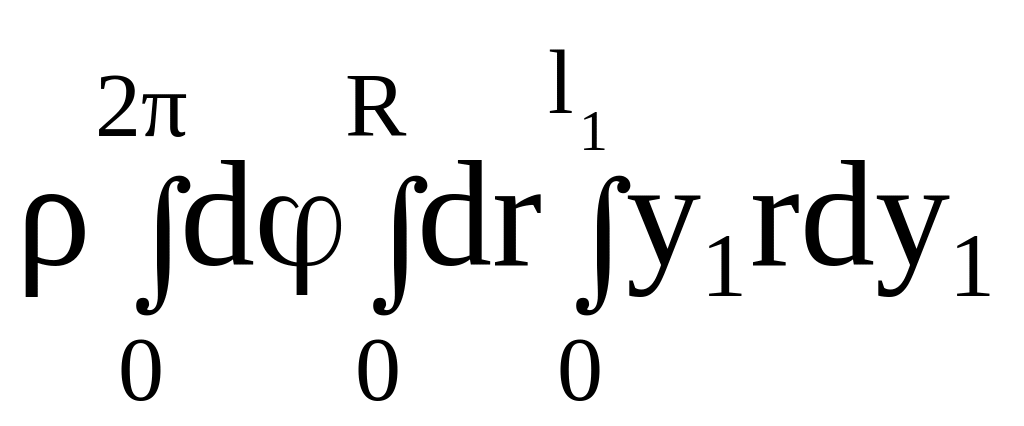 =
=
![]() .
(2.61)
.
(2.61)
В силу симметричности матрицы Hi, (i=1,2,3) имеем
![]() =
=
![]() =
=
![]() =
0, (2.62)
=
0, (2.62)
![]() =
=
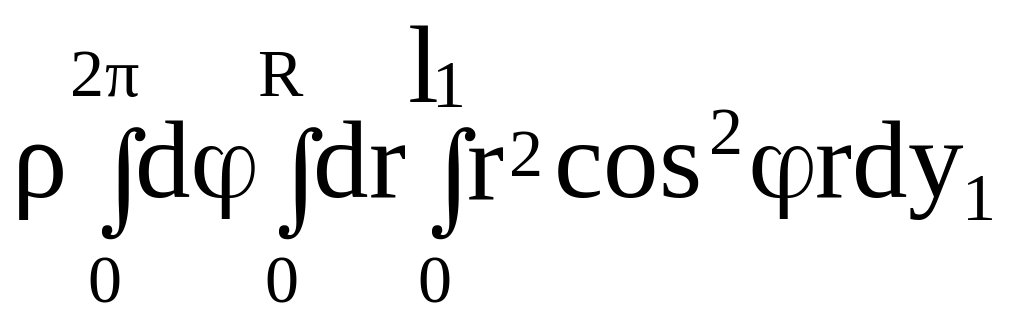 =
=
![]() =
=
![]() =
=
=![]() ,
(2.63)
,
(2.63)
![]() =
=
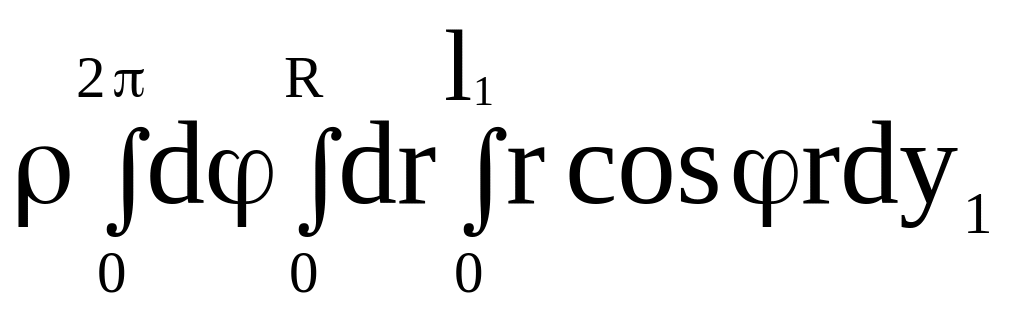 =
0. (2.64)
=
0. (2.64)
Итак,
в соответствии с формулами (2.55)–(2.64)
имеем (учитывая, что
![]() – объем звена 1, а
– объем звена 1, а
![]() – масса звена 1):
– масса звена 1):
H1
=
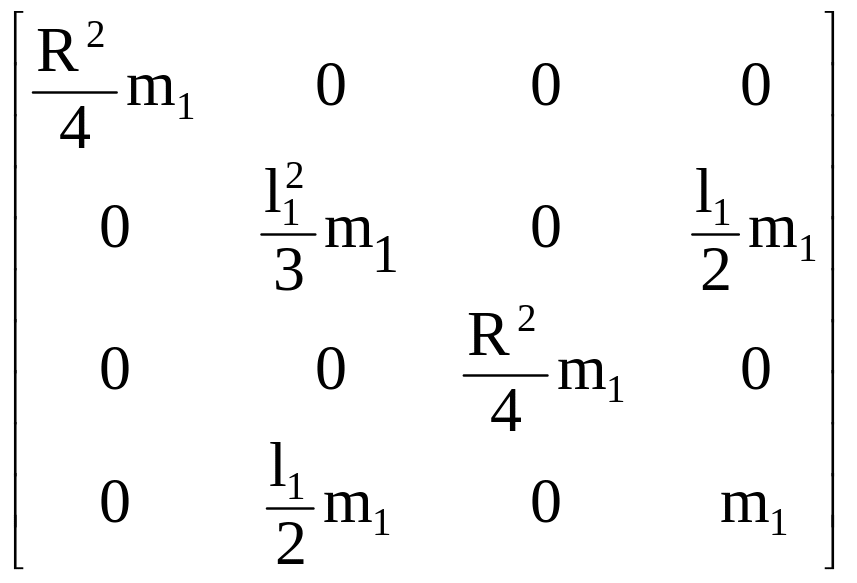 .
(2.65)
.
(2.65)
Звено 2 считаем однородным тонкостенным цилиндром. Взаимное расположение второго звена и системы координат P2x2y2z2 показано на рис. 2.4.
Объемом U2, по которому берутся интегралы для звена 2, является внутренность тонкой стенки.
Переходя к цилиндрическим координатам r, , z2:
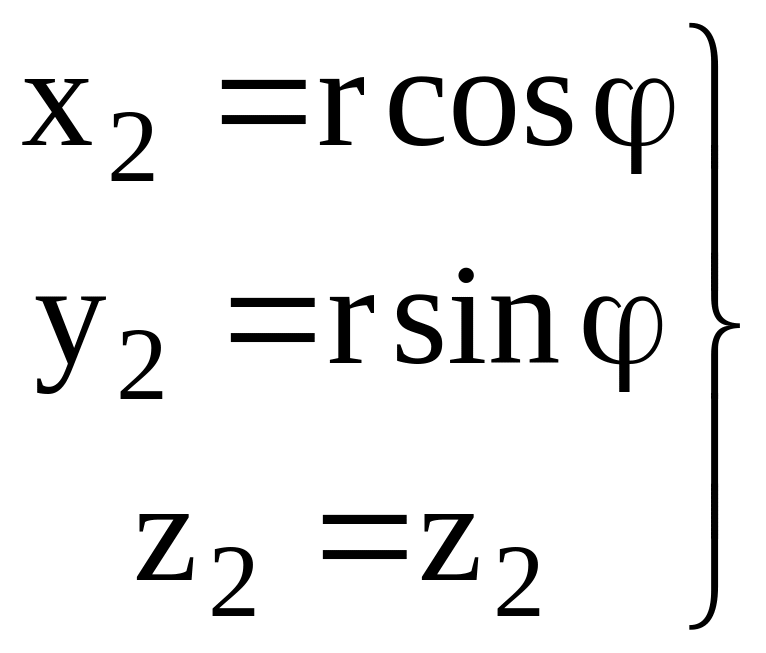
, (2.66)
получаем, что для данного объема U2 и произвольной функции f(x2, y2, z2) интеграл
![]() =
(2.67)
=
(2.67)
преобразуется к виду
![]() =
=
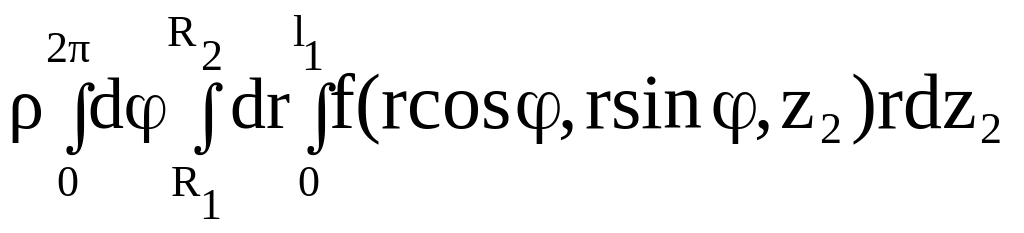 .
(2.68)
.
(2.68)
Подставляя
в формулу (2.68) последовательно функции
![]() ,
y2x2,
z2x2,
x2,
,
y2x2,
z2x2,
x2,
![]() ,
,
![]() ,
z2y2,
y2,
z2
и вычисляя интегралы, имеем
,
z2y2,
y2,
z2
и вычисляя интегралы, имеем
=![]()
![]() =
=
![]() ,
(2.69)
,
(2.69)
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]() =
0, (2.70)
=
0, (2.70)
![]() =
=
![]() =
=
![]() ,
(2.71)
,
(2.71)
![]() =
=
![]() =
=
![]() ,
(2.72)
,
(2.72)
![]() =
=
![]() =
=
![]() ,
(2.73)
,
(2.73)
где m2 – масса звена 2.
Итак, на основании формул (2.69)–(2.73) получаем
H2
=
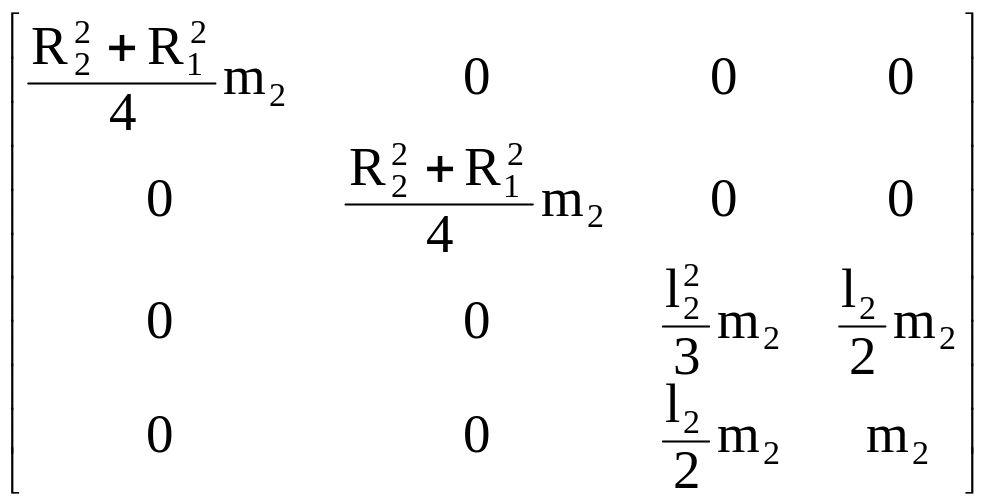 .
(2.74)
.
(2.74)
Для звена 3 взаимное расположение звена (которое считаем сплошным цилиндром длины l3 и радиуса R3) и системы координат P3x3y3z3 представлено на рис. 2.5.
Аналогично (2.68) получаем формулу
![]() =
=
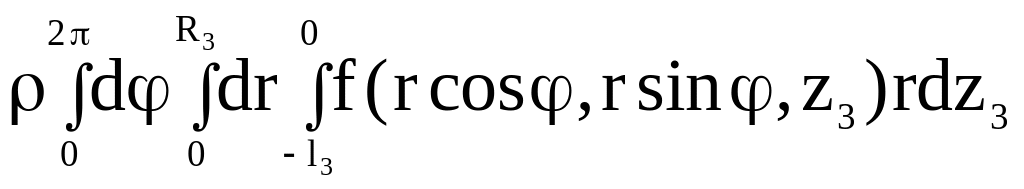 (2.75)
(2.75)
для вычисления элементов матрицы H3.
Проводя эти вычисления аналогично (2.55)–(2.64) и (2.69)–(2.73), получаем
H3
=
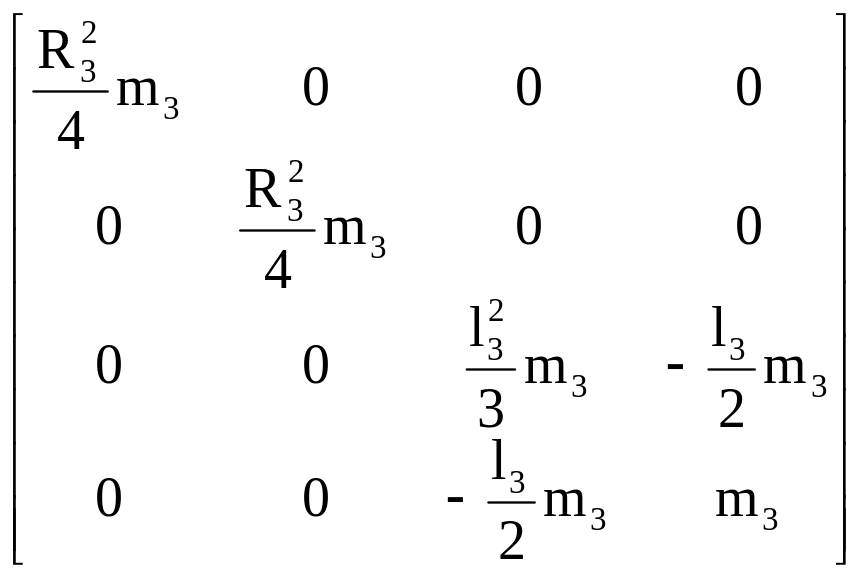 .
(2.76)
.
(2.76)
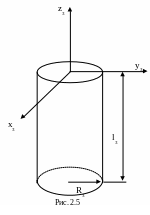
Задача 2. Вычислить кинетическую и потенциальную энергии манипулятора (см. рис. 1.20).
Решение. В соответствии с формулой (2.19) кинетическая энергия манипулятора имеет вид
K
=
![]() .
(2.77)
.
(2.77)
Матрицы
![]() ,
,
![]() ,
,
![]() являются производными матриц S1(q(t))
и S2(q(t)),
задаваемых формулами (1.67), (1.68):
являются производными матриц S1(q(t))
и S2(q(t)),
задаваемых формулами (1.67), (1.68):
![]() =
=
![]() =
=
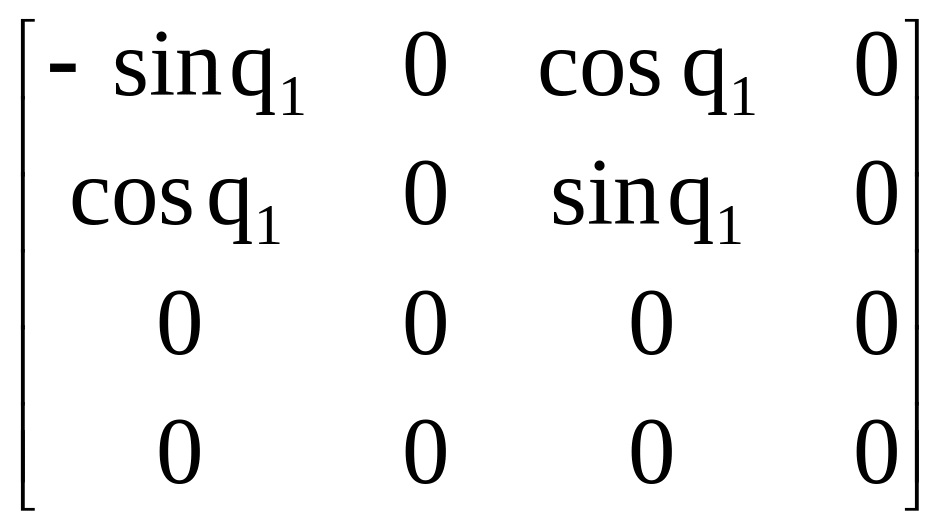 ,
(2.78)
,
(2.78)
![]() =
=
![]() =
=
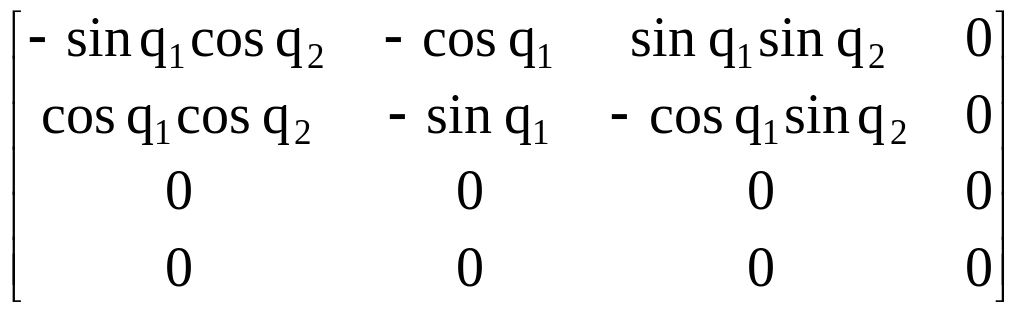 ,
2.79)
,
2.79)
![]() =
=
![]() =
=
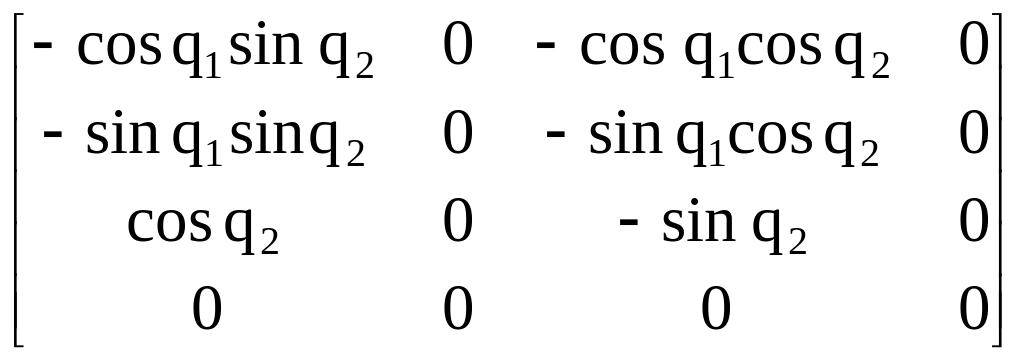 .
(2.80)
.
(2.80)
Подставляя
матрицы в (2.77) и проводя перемножения,
получаем формулу кинетической энергии
манипулятора в зависимости от q1,
q2,
q3,
![]() ,
,
![]() ,
,
![]() .
.
Найдем потенциальную энергию манипулятора в соответствии с формулой (2.26). В нашем случае потенциальная энергия
П
=![]() ,
(2.81)
,
(2.81)
где
g
– ускорение силы тяжести; 3
= (0, 0, 1, 0); mi
(i=1,2,3)
– массы звеньев;
S1,
S2,
S3
– матрицы, определяемые формулами
(1.67)–(1.69);
![]() –
координаты центра масс i-го
звена в системе координат, связанной
со звеном
i.
Считаем, что центры масс расположены
на середине звеньев. Тогда, с учетом
введенных систем координат, имеем
–
координаты центра масс i-го
звена в системе координат, связанной
со звеном
i.
Считаем, что центры масс расположены
на середине звеньев. Тогда, с учетом
введенных систем координат, имеем
![]()
![]()
 (2.82)
(2.82)
![]()
Подставляя (1.67) – (1.69) в (2.81) и проводя вычисления, получаем
П
=![]() .
(2.83)
.
(2.83)
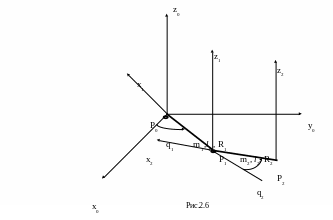
Задача 3. Вывести уравнение динамики для манипулятора, состоящего из двух звеньев (рис. 2.6).
Массы первого и второго звеньев равны, соответственно, m1 и m2, длины звеньев – l1 и l2, радиусы – R1 и R2. Звенья считаем сплошными однородными цилиндрами. Все движение происходит в плоскости x0P0y0.
Решение. Уравнение динамики имеет вид (2.84). По этому уравнению можно узнать, как изменяются обобщенные силы, если известно, как изменяются обобщенные координаты. Кроме того, можно узнать, как изменяются обобщенные координаты, если известно, как изменяются обобщенные силы.
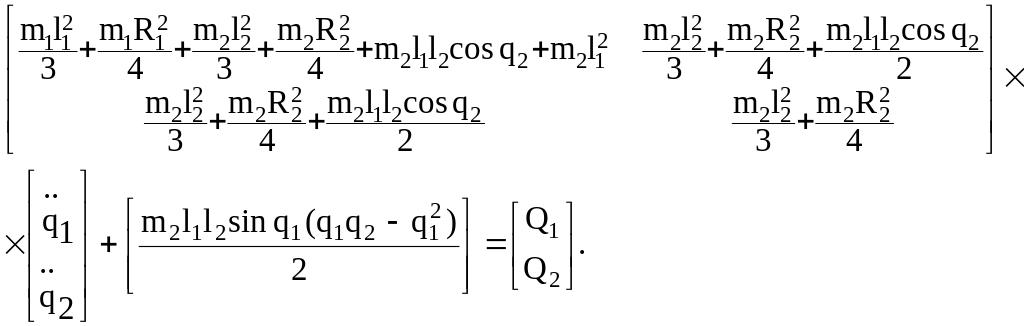 (2.84)
(2.84)
