Библиографический список

1. Лопатин П.К., Звягин П.А., Применение в точном алгоритме управления манипуляционными роботами в неизвестной среде алгоритмов полного перебора и фронта распространения волны// Актуальные проблемы защиты и безопасности. Экстремальная робототехника. Труды Девятой Всероссийской научно-практической конференции. Том 5. НПО Специальных материалов. Санкт-Петербург. 2006, стр.307-313.

2. Barraquand J., Latombe J.-C. Robot Motion Planning: A Distributed Representation Approach // Int. J. of Rob. Res., Vol. 10, No. 6, December 1991. — Pp. 628–649.

3.6.5. Алгоритм полиномиальной апроксимации

Рассмотрим алгоритм полиномиальной аппроксимации [2]. Пусть дано n-мерное пространство конфигураций, в котором имеются запрещённые точки p₁, p₂, …, p_M. Необходимо найти путь в пространстве обобщённых координат, описываемый вектор-функцией q(t), который соединял бы заданные начальную точку q⁰ и целевую точку q^T, ни одной своей точкой не налегал бы ни на одну из запрещённых точек и удовлетворял бы ограничению q^L ≤ q(t) ≤ q^H. Пусть t [t₀; T], t₀ = 0, T = 1, q(0) = q⁰ и q(1) = q^T.

Пространство обобщённых координат дискретизировано с шагом Δq по всем координатам, т.е. q может принимать только значения, попадающие в узлы n-мерной сетки. Найденный путь должен представлять последовательность q⁰, q¹, …, q^T, соседние элементы которой должны отличаться не более чем на один шаг по каждой координате.

Обозначим компонеты вектор-функции q(t) = (q₁, q₂,…, q_n), тогда ограничения примут следующий вид:

q_j(0) = q⁰_j, q_j(1) = q^T, j = 1, 2, … , n. (3.109)

q^L_j ≤ q_j(t) ≤ q^Н_j, j = 1, 2, ... , n. (3.110)

Препятствия зададим в виде гиперсфер с центром в точках (q^p_m1, q^p_m2, … , q^p_mn) и радиусом r = (Δq / 2) ∙ 1.1, где q^p_mi есть соответствующие компоненты векторов p_m, m = 1, 2, …, M. Тогда условие неналегания пути на препятствия можно записать так:

(3.111)

Будем искать путь в виде полиномов некоторой степени s:

, (3.112)

здесь c_ji – неизвестные коэффициенты, требующие определения.

Подставим в (3.112) значения t = 0 и t = 1:

q_j(0) = c_j0 + c_j1 ∙ 0 + c_j2 ∙ 0² + … + c_js ∙ 0^s = c_j0

q_j(1) = c_j0 + c_j1 ∙ 1 + c_j2 ∙ 1² + … + c_js ∙ 1^s = c_{j0 +} , (3.113)

j = 1, 2, …, n.

С учётом ограничений (3.109) можно записать:

c_j0 = q⁰_j (3.114)

= q^T_j – q⁰_j , j = 1, 2, …, n (3.115)

Разобьём отрезок времени [0; 1] на K + 1 отрезков, получив между t = 0 и t = 1 K промежуточных точек t₁, t₂, …, t_K. Тогда ограничения (3.110) и (3.111) запишутся в следующем виде:

≥ q^L_{j ,} j = 1, 2, …, n

≤ q^H_{j ,} j = 1, 2, …, n (3.116)

≥ r²,

m = 1, 2, …, M, k = 1, 2, …, K.

Таким образом, необходимо найти такие коэффициенты c_ji (при j = 1, 2, …, n; i = 1, 2, …, s), которые являются решением системы уравнений (3.114), (3.115) и неравенств (3.116). Очевидно, коэффициенты c_j0 легко находятся из уравнений (3.114). Выразим из уравнений (3.115) коэффициенты c_js:

Подставим c_j0 и c_js в (3.116):

(3.117)

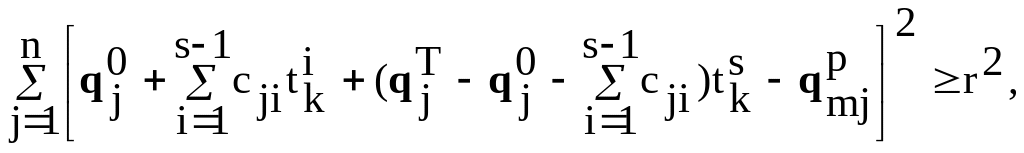
Итак, необходимо решить систему из (M + 2n)·K нелинейных неравенств. Эту задачу можно свести к задаче оптимизации некоторой функции F(C):

(3.118)

где C – вектор коэффициентов (c_1,1, c_1,2, …, с_1,s-1, c_2,1, c_2,2, …, с_2,s-1,…, c_n,1, c_n,2, …, c_n,s-1), задающий путь, E(C) – мера нарушения ограничений путём, P(C) – оценка вероятности того, что путь не налегает на неизвестные препятствия.

Зададим функцию E(C). Ввведём функцию, определяющую j-ю координату точки траектории, заданной вектором C, в момент времени t:

(3.119)

Зададим функции, соответствующие неравенствам системы ограничений и показывающие нарушение нижней и верхней границ и налегание на препятствия траектории в момент времени t:

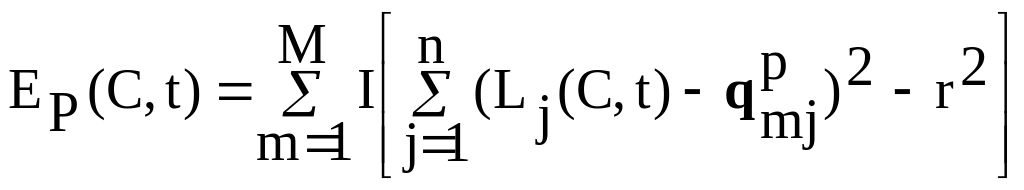(3.120)

Теперь объединим все ограничения в одну функцию (с учётом всех дискретных моментов времени, за исключением t = 0 и t = 1):

. (3.121)

Таким образом, функция E(C) принимает отрицательные значения, если хотя бы одно ограничение нарушено, и устанавливается в ноль в противном случае, т.е. если вектор коэффициентов C удовлетворяет всем неравенствам системы (3.117).

Для того чтобы можно было сравнить двапути, не нарушающие ограничения и не налегающие на препятствия, была введена функция P(C), значение которой – оценка вероятности того, что путь не налегает на неизвестные препятствия. Она вычисляется следующим образом. Будем считать, что вероятность встретить неизвестное препятствие в некоторой точке равна

p(d) = e^-2d, (3.122)

где d – расстояние до ближайшего известного препятствия.

Тогда

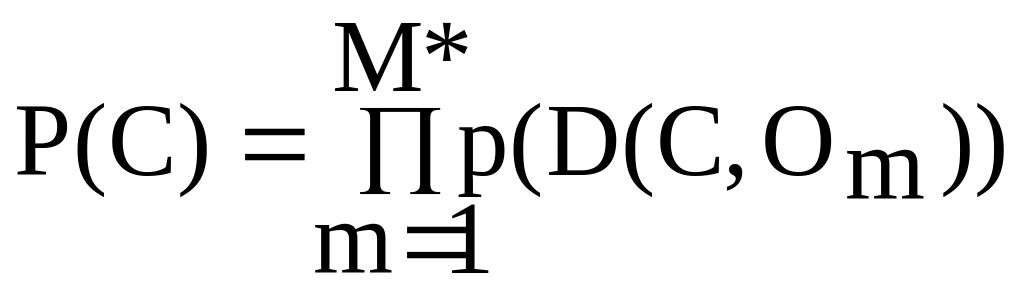, (3.123)

где {O₁, O₂, …, O_M*} – множество препятствий, мимо которых пролегает траектория, – расстояние от пути С до препятствия O.

Мимо препятствия O проходит путь, если найдётся такая точка пути L(t_k), что для неё препятствие O ближе, чем остальные препятствия. Использование функции P(C) будет способствовать тому, чтобы алгоритм генерировал пути, которые проходят, по возможности, далеко от обнаруженных препятствий.

Для оптимизации функции F(C) предлагается использовать генетический алгоритм. В основе генетического алгоритма [1] лежит коллективный процесс обучения внутри популяции индивидов, каждый из которых представляет собой поисковую точку пространства. В нашем случае таким пространством является пространство векторов C. Кодирование вектора в индивиде осуществляется следующим образом. По каждой компоненте вектора задаётся интервал, значения из которого она принимает. Этот интервал разбивается на некоторое количество дискретных узлов. Таким образом, каждой компоненте вектора сопоставляется номер узла, соответствующий её значению. Индивид образуется последовательностью этих номеров в бинарном представлении.

Общая схема алгоритма:

1. Генерация случайным образом начальной популяции.

2. Вычисление пригодности индивидов.

3. Селекция индивидов в промежуточную популяцию.

4. С вероятностью P_c выбрать случайным образом из промежуточной популяции двух индивидов, произвести скрещивание и потомка поместить в популяцию потомков; а с вероятностью 1-P_c выбрать случайным образом из промежуточной популяции индивида и поместить его в популяцию потомков.

5. Если размер популяции потомков меньше N, перейти на шаг 4.

6. Инвертировать каждый бит каждого индивида из популяции потомков с заданной вероятностью мутации P_м.

7. Популяция потомков переходит в следующее поколение.

8. Если еще не прошло нужное количество поколений, перейти на шаг 2.

На 3-ем этапе применяется турнирная селекция. В качестве пригодности индивидов используется функция F(C). В процессе селекции проводится N турниров (N – размер популяции) среди случайно выбранных m индивидов (m – размер турнира), наилучший из которых переходит в следующее поколение.

На 4-ом этапе применяется арифметическое скрещивание. Из двух родителей получается один потомок, компоненты которого находятся как среднее арифметическое соответствующих компонент родителей.

После того, как найдены коэффициенты полиномов, определяющих путь, необходимо получить последовательность дискретных точек этого пути q⁰, q¹, …, q^T. Первая точка (q⁰) известна из исходных данных. Остальные точки найдём по следующему алгоритму:

1. t = 0; i = 0.

2. t_H = 1.

3. t* = (t + t_H) / 2.

4. Определить точку q* c координатами (q*₁, q*₂, …, q*_n), в окрестности которой лежит путь в момент времени t*:

q*_j - q/2 ≤ q_j(t*) < q*_j + q/2, j = 1, 2, …, n.

5. Если q* совпадает с q_i, то t = t*, перейти на шаг 3.

6. Если q* не является соседней по отношению к q_i, то t_H = t*, перейти на шаг 3.

7. Если q* не является запрещённой, перейти на шаг 9.

8. Если q_ij - q ≤ q_j(t*) ≤ q_ij + q j = 1, 2, …, n, где q_ij – координаты точки q_i, то t = t*, иначе t_H = t*. Перейти на шаг 3.

9. i = i + 1; q_i = q*.

10. Если qⁱ = q^T, алгоритм завершён, иначе перейти на шаг 2.

Алгоритм полиномиальной аппроксимации применим для n-мерного пространства состояний, но не гарантирует нахождения пути.