Алгоритм

Перед началом работы Алгоритма n=0 и, соответственно, qⁿ=q⁰.

ШАГ1. При нахождении МР в qⁿ, n=0,1,2,… его СС доставляет информацию об r-окрестности точки qⁿ и формируются множества Y(qⁿ), Z(qⁿ), Q(qⁿ). Затем вызывается процедура ПИ (qⁿ, q^T, ), которая генерирует путь L(qⁿ, q^T). Переход на ШАГ2.

ШАГ2. МР начинает двигаться вдоль L(qⁿ, q^T). При движении по L(qⁿ, q^T) возможны два исхода:

а) МР не встретит ранее неизвестных запрещённых состояний и, как следствие, достигнет q^T. По достижении q^T Алгоритм заканчивает свою работу.

б) МР придёт в такую точку (предварительно выполнив n:=n+1, обозначим её qⁿ, n=1, 2,…), что следующая точка исполняемого пути является запрещённой. Переход на ШАГ1. Конец Алгоритма.

Теорема. Если МР будет двигаться по вышеприведенному Алгоритму, то он перейдет из q⁰ в q^T за конечное число шагов.

Доказательство. Так же, как и в доказательстве [ису20011] необходимо показать, что число точек смены пути будет конечным и они все будут различными.

Показывается, что они различные.

Что их число конечно.

Поскольку число точек смены пути конечно, то в последней точке смены пути МР спланирует новый путь, при исполнении его не появится новая точка смены пути и q^T будет достигнута за конечное число шагов в силу конечности длины пути.

Результаты моделирования

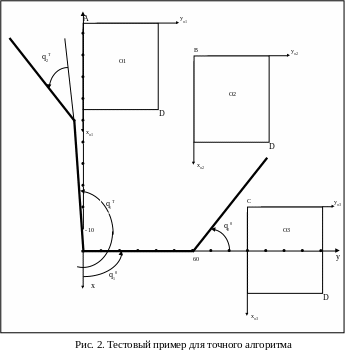
Разработано программное обеспечение (ПО) на основе точного алгоритма. Приведем результаты работы ПО на следующем тестовом примере (Рис. 2). Требовалось передвинуть плоский двузвенный манипулятор из q⁰=(1.57; 0.8)(радиан) в q^T=(3.2; 0.8)(радиан). Манипулятор движется в плоскости xOy. Длина каждого звена составляет 60 пикселов. В рабочей зоне имеется три прямоугольных препятствия: O1, O2 и O3. Координаты начал A, B, C систем координат, связанных с препятствиями O₁, O₂, O₃ соответственно, в базовой системе координат составляют: (x^A= -105, y^A=0), (x^B= -90, y^B=60), (x^C= -20, y^C=0). Координаты точки D каждого из препятствий определены в системе координат, привязанной к препятствию, и в каждой из этих систем равны (x^D=40, y^D=40). Гиперпараллелепипед (1) для д анного случая предстает в виде (2) (числа даны в радианах).

Мы уже упоминали о том, что задача управления манипуляторами в неизвестной среде сводится к решению конечного числа задач планирования траектории манипулятора в среде с известными запрещенными точками. В качестве алгоритма для решения задачи планирования траектории в известной среде мы выбрали алгоритм полного перебора [9, стр.55]. Поскольку этот алгоритм может быть применен только для дискретизированного пространства конфигураций, введем дискретизацию. Величина delta дискрета по каждой обобщенной координате q_i, i=1,2, вычисляется следующим образом:

delta=(0+6.28)/количество_дискретов (3),

то есть мы суммируем минимальную и максимальную величины по i-той обобщенной координате и делим результат на количество дискретов, лежащих между минимальной и максимальной величинами по i-той (i=1,2) обобщенной координате. Время работы точного алгоритма для различных delta приведено в Таблице 1. Программное обеспечение написано на языке C и тестировалось на процессоре AMD Athlon XP 1800+ 1.533 GHz. Как можно видеть, цель достигалась во всех случаях, но использование алгоритма полного перебора ведет к существенным временным затратам с уменьшением delta.

В связи с этим требуется либо модифицировать алгоритм полного перебора, учитывая, что поначалу запрещенных точек обнаружено немного, либо использовать другие алгоритмы в качестве алгоритма планирования траектории в среде с известными запрещенными состояниями.

Таблица 1.

№	delta, ˚	t, секунд		№	delta, ˚	t, секунд
1	9	67		6	3	159
2	8	74		7	2	412
3	6	81		8	1.5	1139
4	4.5	94		9	1	5968

На Рис.3. приведены все конфигурации из пути движения манипулятора к целевой конфигурации (для случая delta=9˚).

Работа сенсорной системы имитировалась программой. Для текущей конфигурации qⁿ (n=0,1,2,…) Y(qⁿ) представляло собой 3ⁿ-1 соседних к qⁿ конфигураций. На каждом звене выделялось 20 точек. Конфигурация заносилась в множество Z(qⁿ), если ни одна точка ни одного звена не принадлежала внутренней области ни одного препятствия и она удовлетворяла ограничениям (1), в противном случае конфигурация заносилась в Q(qⁿ).

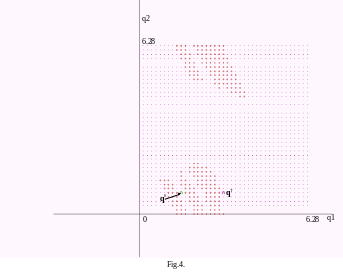
Теперь рассмотрим движение манипулятора в конфигурационном пространстве. На Fig.4. показано конфигурационное пространство, определенное условиями 0<=qi<=6.28 rad, i=1,2. Разрешенные конфигурации показаны маленькими точками, конфигурации, пересекающиеся с препятствиями, показаны жирными точками. Таким образом, мы показываем все запрещенные конфигурации из конфигурационного пространства и наблюдатель (но не робот) может видеть все существующие запрещенные точки.

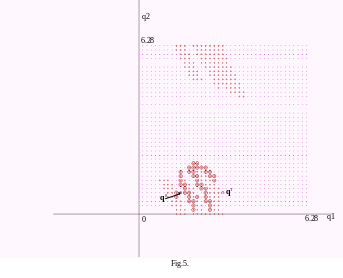
На Fig.5. показаны все запрещенные конфигурации, обнаруженные манипулятором во время его движения. Они показаны окружностями вокруг жирных точек. Таким образом, манипулятор обнаружил только некоторые из объективно существующих запрещенных точек.

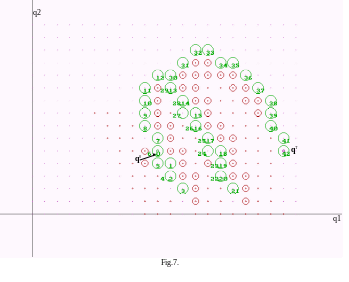
На Fig.6. приведен путь, пройденный манипулятором. Он показан окружностями вокруг обычных точек, что закономерно, поскольку путь состоит из разрешенных точек. На Fig.7. путь показан в увеличенном виде.

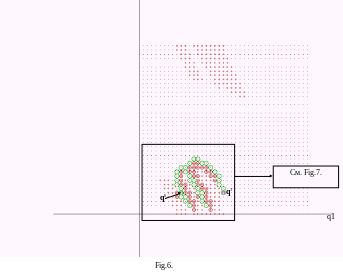
q2

очки пути пронумерованы, точка q⁰ имеет номер 0, точка q^T имеет номер 42.