3.4. Планирование траектории с учетом динамики манипулятора

Методы планирования траектории, приведенные в предыдущих параграфах, имеют следующий недостаток: пусть мы нашли q(t), но когда подставим q(t) в уравнение динамики манипулятора

A(q(t), c) (t) + b(q(t), (t), c) = Q(t), (3.50)

то могут нарушиться условия

Q_н  Q(t)  Q_в (3.51)

в один или более моментов времени t. Здесь Q_н – нижние ограничения на обобщенные силы, Q_в – верхние ограничения.

Поэтому более приближенной к реальности была бы другая постановка задачи: найти вектор q(t), удовлетворяющий условиям

q(t₀) = q⁰, (3.52)

q(T) = q^T, (3.53)

a¹  q(t)  a², (3.54)

b¹  (t)  b², (3.55)

w¹  (t)  w², (3.56)

A(q(t), c) (t) + b(q(t), (t), c)  Q_в, (3.57)

-[A(q(t), c) (t) + b(q(t), (t), c)] –Q_н (3.58)

для каждого t[t₀,T].

Решать эту задачу можно с помощью теории оптимального управления.

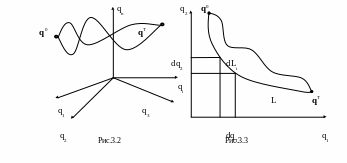
Сведение к задаче оптимального управления. Перед нами стоит задача: найти в пространстве обобщенных координат линию, соединяющую q⁰ и q^T. Таких линий может быть бесконечное множество (рис. 3.2). Надо выбрать какую-то одну линию, и при этом возникает желание выбрать наилучшую (оптимальную), причем в каком-то смысле – иногда нужна самая короткая, иногда – требующая минимального расхода энергии, иногда – удовлетворяющая одновременно нескольким требованиям. Требование оптимальности надо научиться записывать в математическом виде. Поясним это на двумерном примере. Пусть нам надо выбрать траекторию с минимальной длиной (рис. 3.3). Для рассмотрения выберем наугад какую-нибудь линию. Ее длину обозначим L. Длина dL_i маленького кусочка линии (этот кусочек считаем отрезком прямой) вычисляется по теореме Пифагора:

(dL_i)² = (dq₁)² + (dq₂)². (3.59)

Но, согласно определению производной, dq_i = dt, тогда

dL_i = dt. (3.60)

Длина всей линии складывается из этих кусочков:

L = dL₁ + dL₂ + ... + dL_N = = =

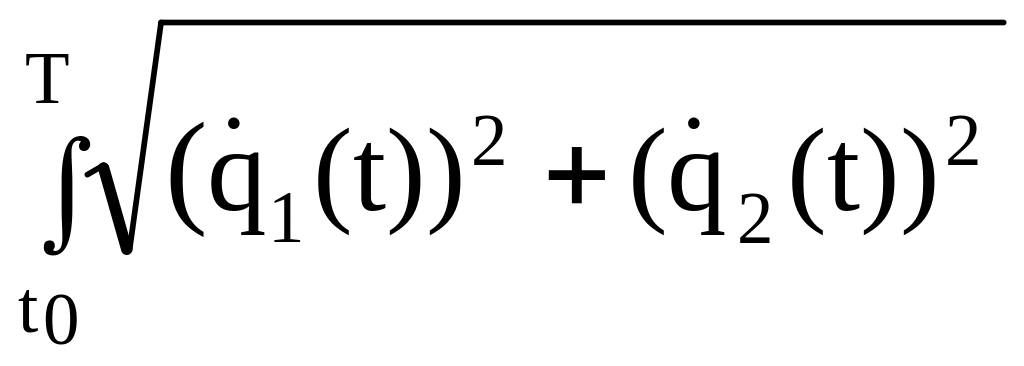= dt. (3.61)

В n-мерном случае квадрат длины элементарного кусочка

(dL_i)² = (dq₁)² + (dq₂)² + ... + (dq_n)². (3.62)

Тогда

dL_i = dt. (3.63)

И длина всей линии

L = dL₁ + dL₂ + ... + dL_N = = =

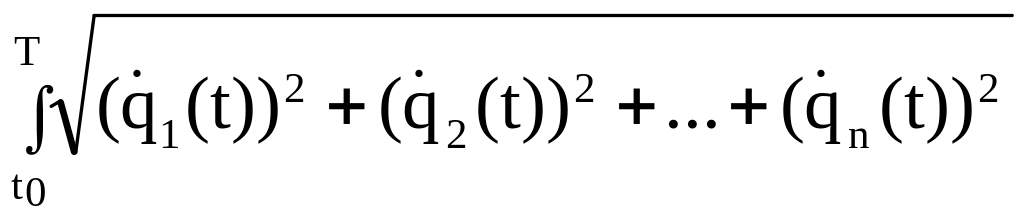= dt (3.64)

или, в других обозначениях,

L = q(t), t)dt. (3.65)

Разные линии описываются разными вектор-функциями q(t). Будем подставлять разные формулы для q(t) и получать разные L, сообщающие нам о длине траектории. Поэтому требование об определении кратчайшей траектории математически можно сформулировать так: найти такую вектор-функцию q(t), при которой величина L будет принимать минимальное значение из всех возможных. Функция L называется функционалом.

Точно так же требование оптимальности в каком-либо другом аспекте выражают в виде требования найти вектор-функцию, сообщающую минимум соответствующему функционалу.

Для дальнейшего изложения необходимо привести уравнение динамики манипулятора (2.50) к нормальной форме. Для этого запишем его в следующем виде:

(t) = A^-1(q(t), c)[Q(t) - b(q(t), (t), c)], (3.66)

где A^–1(q(t), c) – матрица, обратная к A(q(t), c).

Предполагаем, что A^–1(q(t),c) существует в каждый момент времени t[t₀,T].

Введем обозначения (3.67) и тогда, используя формулы (3.66) и (3.67), получим (3.68):

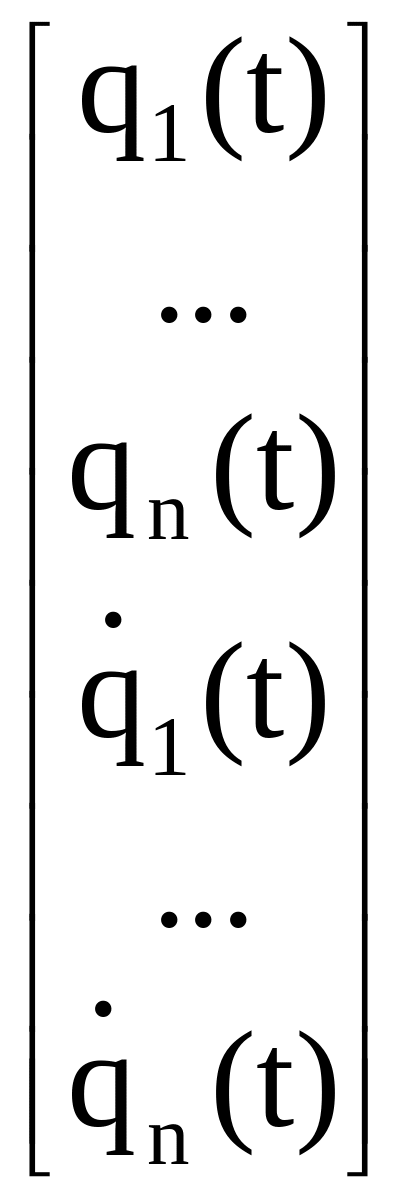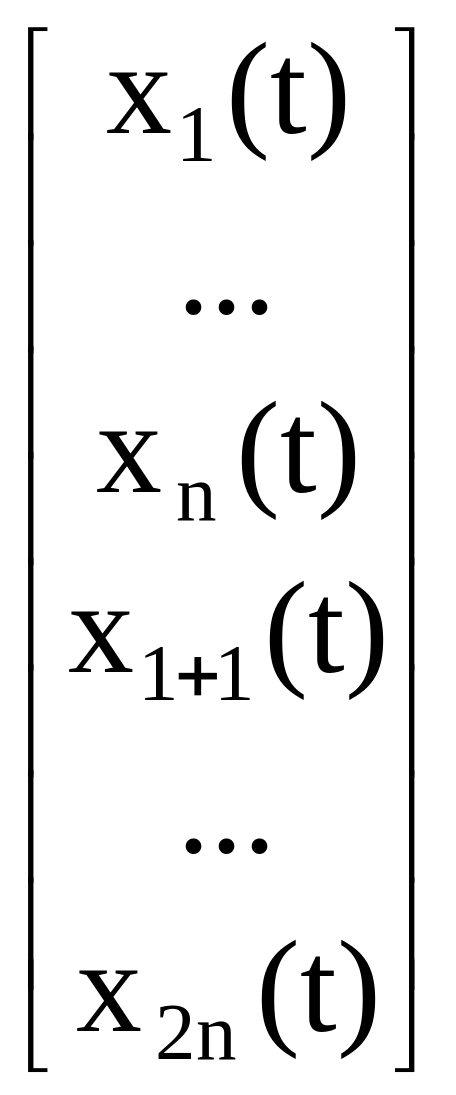= = x(t), Q(t) = u(t), (3.67)

= =

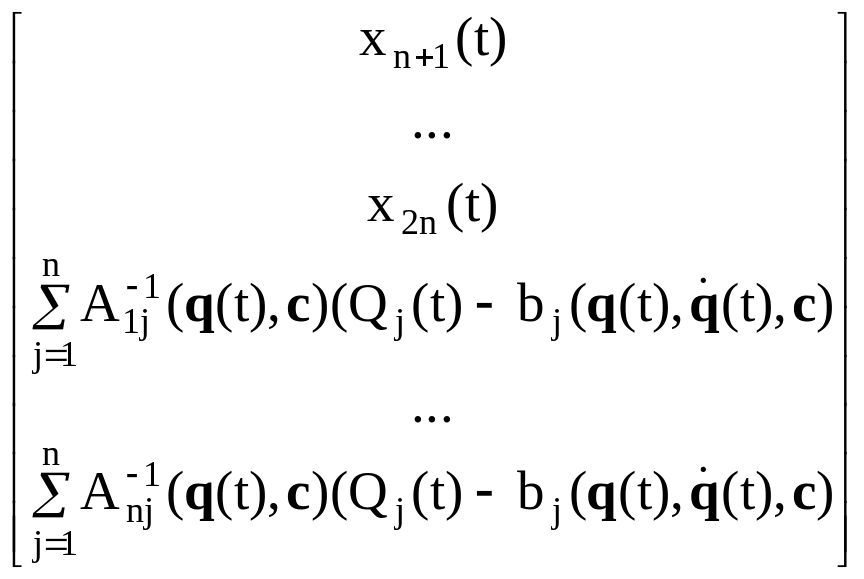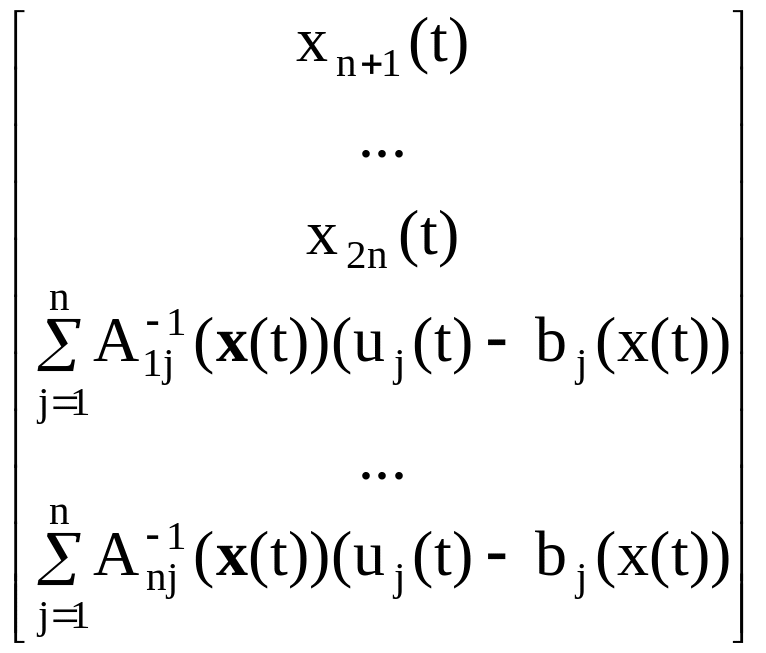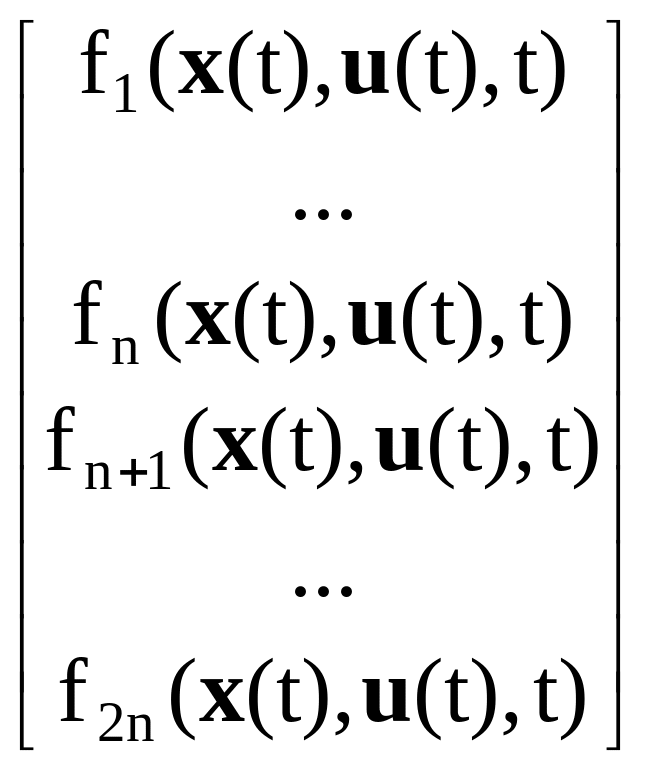= = . (3.68)

Запишем (3.68) в векторном виде:

(t)= f(x(t), u(t), t). (3.69)

Уравнение (3.69) представляет собой систему из 2n обыкновенных дифференциальных уравнений первого порядка и называется уравнением динамики в нормальной форме.

Как было сказано выше, q(t), (t), (t) не могут принимать произвольных значений, что можно выразить математически:

x(t)G_x, (3.70)

u(t)G_u, (3.71)

t[t₀, T], (3.72)

где G_x, G_u – некоторые множества.

Теперь мы можем сформулировать задачу оптимального управления: найти такие x(t) и u(t), которые удовлетворяли бы уравнению динамики

(t) = f(x(t), u(t), t), (3.73)

краевым условиям

x(t₀) = x⁰, (3.74)

x(T) = x^T, (3.75)

ограничениям

x(t)G_x, (3.76)

u(t)G_u, (3.77)

t[t₀, T], (3.78)

и сообщали минимум некоторому функционалу

J = x(t), u(t), t)dt, (3.79)

где минимизация функционала выражает требование оптимальности в каком-то аспекте.

Следует сказать, что до сих не предложено методов, гарантирующих решение этой задачи. Однако в 1956 г. Л. С. Понтрягин сформулировал необходимое условие оптимальности (называемое также принципом максимума Понтрягина [1]), позволяющее в некоторых случаях находить оптимальное управление.

Принцип максимума Понтрягина в поиске оптимальных траектории и управления. Выведем численную схему поиска оптимальных траектории и управления. Пусть требуется найти такие x(t) и u(t), которые бы удовлетворяли уравнению динамики (3.73), краевым условиям (3.74), (3.75), ограничениям (3.76)-(3.78) и сообщали бы минимум функционалу (3.79).

Обозначим функционал (3.85) через следующую формулу:

x₀(t) = x(t), u(t), t)dt. (3.80)

Тогда

= f⁰(x(t), u(t), t). (3.81)

Теперь будем рассматривать (n+1)-мерный вектор

(t) = (x₀(t), x₁(t), ... , x_n(t)). (3.82)

Кроме того, будем рассматривать вектор неизвестных функций:

(t) = (₀(t), ₁(t), ... , _n(t)), (3.83)

но таких, что

= – ₀(t) – ₁(t) – ... – _n(t) . (3.84)

Запишем функцию H, называемую гамильтонианом:

H( (t), (t), u(t)) = ₀(t)f⁰(x(t), u(t), t) + ₁(t)f₁(x(t), u(t), t) + ...+

+ _n(t)f_n(x(t), u(t), t). (3.85)

Теперь мы можем сформулировать сам принцип максимума Понтрягина: оптимальное управление придает функции H максимум в каждый момент времени t[t₀, T].

Поясним смысл этого принципа. Рассмотрим всевозможные управления u(t), и пусть нам откуда-то известно, что u^*(t) – оптимальное управление. Тогда для любого u(t) и для любого t будет верно неравенство

H(u^*(t))  H(u(t)).

Путем непосредственной проверки можно убедиться в том, что

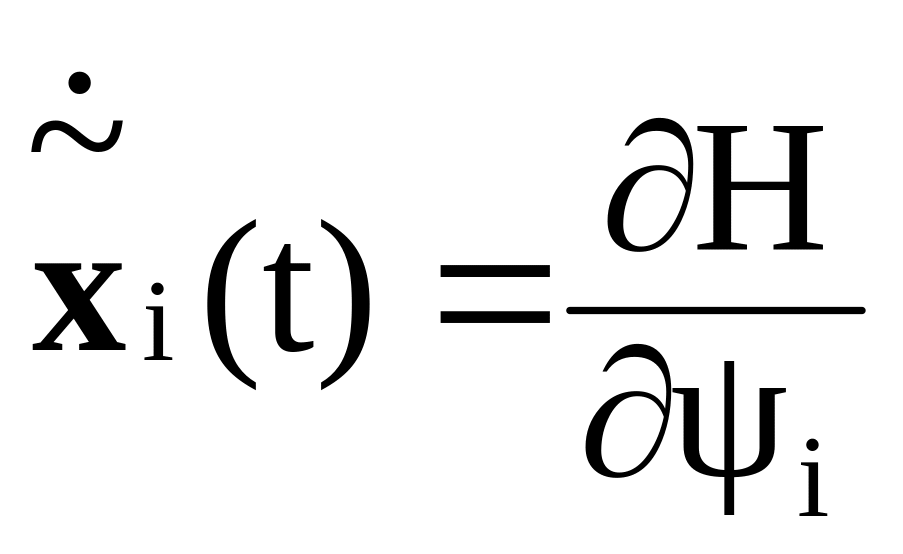, i = 0,1, ... , n (3.86)

и

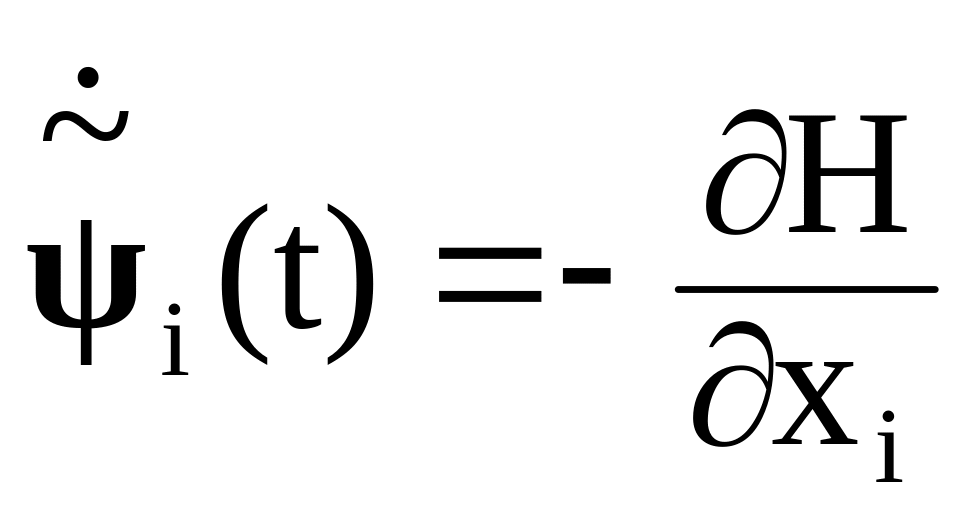, i = 0,1, ... , n. (3.87)

Согласно определению производной,

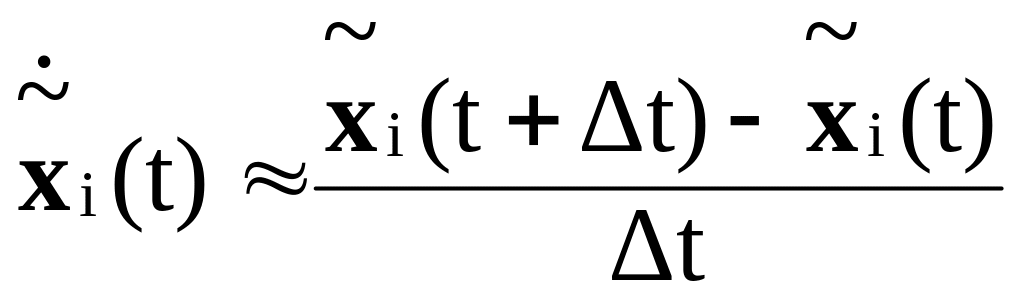= |в других обозначениях| =

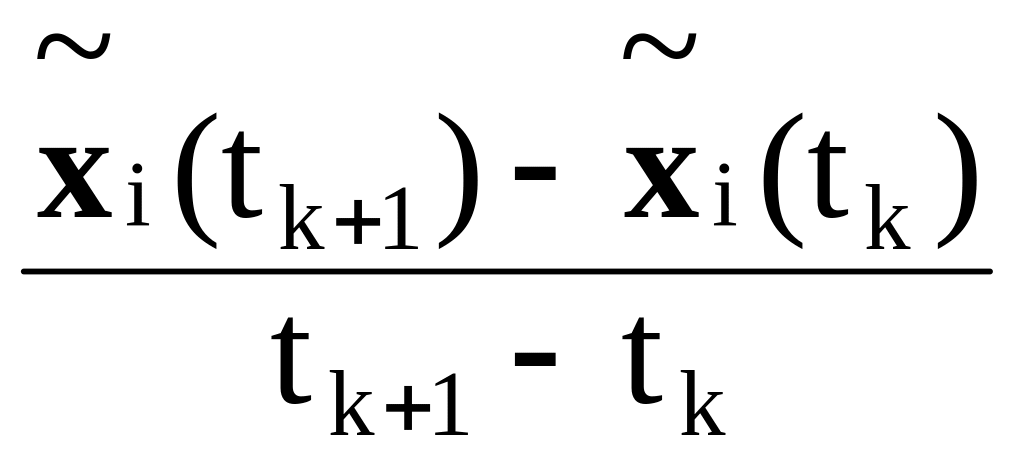= , i = 0,1,…,n. (3.88)

По аналогии с (3.88)

, i = 0,1, … , n. (3.89)

Заметим также, что и есть некоторые функции. Обозначим = ( (t), (t), u(t)) и = ( (t), (t), u(t)). Тогда система (3.86) – (3.87) примет вид

( t_k), (t_k), u(t_k))(t_k+1– t_k), i = 0,1, ... , n, (3.90)

( t_k), (t_k), u(t_k))(t_k+1– t_k), i = 0,1, ... , n. (3.91)

Формулы (3.90)–(3.91) и представляют численную схему расчета оптимальных траектории и управления. Опишем порядок ее использования.

Пусть k = 0. Вектор (t₀) известен:

(t₀) = x⁰,

а вектор (t₀) неизвестен. Придадим его компонентам произвольные значения. Функции и зависят также от u(t). Вектор u(t₀) тоже неизвестен. Определим его, используя принцип максимума, т. е. найдем тот вектор чисел u(t₀), который придает функции H в момент t₀ максимум (эта задача решается методами оптимизации) и удовлетворяет условию (3.77). Если такое управление найти невозможно, то задача нахождения оптимальных траекторий и управления в данном случае не может быть решена. Определив u(t₀), получим оптимальное управление в момент t₀. Затем подставим (t₀), (t₀), u(t₀) в систему уравнений (3.90)–(3.91) и получим (t₁) и (t₁). Проверяем, удовлетворяет ли (t₁) условию (3.76). Если нет, то задача нахождения оптимальных траекторий и управления в данном случае не может быть решена. Если да, то выполняем k = k + 1 и переходим к поиску (t_K), (t_K), (t_K).

Вычисляя (t₀), (t₁), ..., получим, наконец, (T). Может оказаться, что мы получим

(T)  ^T,

т. е. оптимальная траектория и, соответственно, оптимальное управление, найдены не будут. Это происходит из-за того, что (t₀) был неизвестен, и мы взяли его произвольным. В этом случае надо взять вектор

+

и повторить процесс. Проблема в том, что мы не знаем, как правильно выбрать  . Попытки решения этой проблемы обсуждаются [1].

Если же мы вычислим ( (t), u(t)), удовлетворяющие требованиям (3.73) – (3.79), то тем самым мы найдем (q(t), Q(t)), переводящие манипулятор из q⁰ в q^T оптимальным образом.