1.3. Кинематика поступательного движения тела

относительно неподвижной системы координат

Рассмотрим случай, когда система P_ixyz движется поступательно относительно неподвижной системы P_i-1x_i-1y_i-1z_i-1 (рис. 1.8).

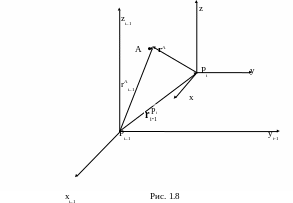
Нам известны законы изменения координат точки А в системе P_ixyz. Они описываются вектором r^A:

r^A = . (1.18)

Мы хотим вычислить координаты точки А в системе P_i-1x_i-1y_i-1z_i-1. Эти координаты будут описываться вектором r_i-1^A:

r_i-1^A = . (1.19)

В соответствии с рис. 1.8 получаем следующее выражение:

r_i-1^A = + r^A, (1.20)

или, покоординатно,

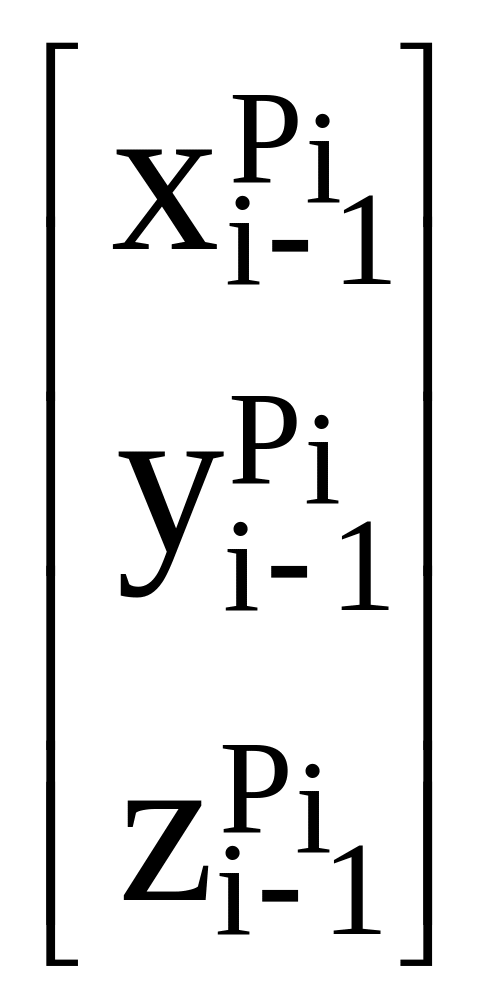= + . (1.21)

С помощью формулы (1.21) можно вычислить координаты произвольной точки в (i–1)-й системе координат, если мы знаем, как изменяются координаты этой точки в системе O_ixyz.

1.4. Кинематика произвольного движения твердого тела

относительно неподвижной системы координат

Мы ставили перед собой задачу: зная координаты некоторой точки А в системе P_ix_iy_iz_i, произвольно движущейся относительно неподвижной системы P_i-1x_i-1y_i-1z_i-1, научиться вычислять координаты точки А в системе P_i-1x_i-1y_i-1z_i-1. В результате наших исследований мы получили формулы (1.9) и (1.21). Преобразуя их, получаем:

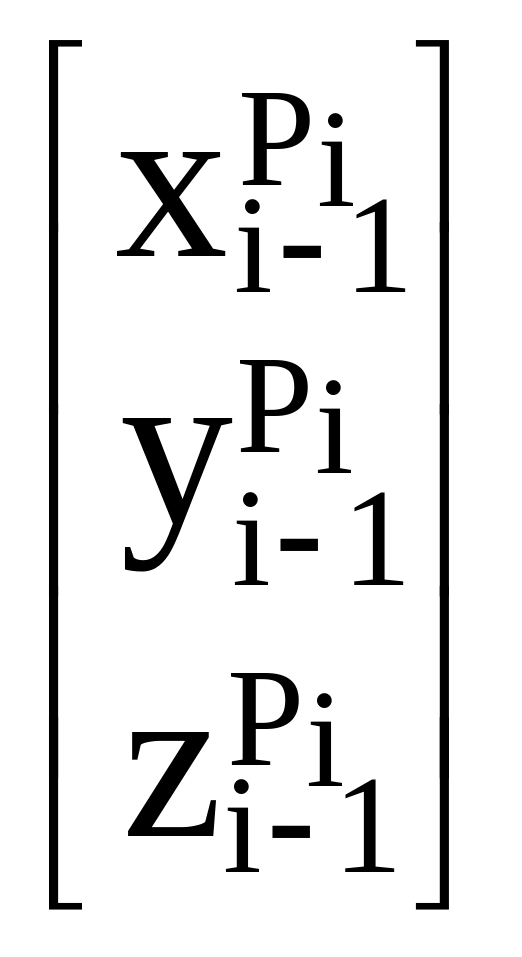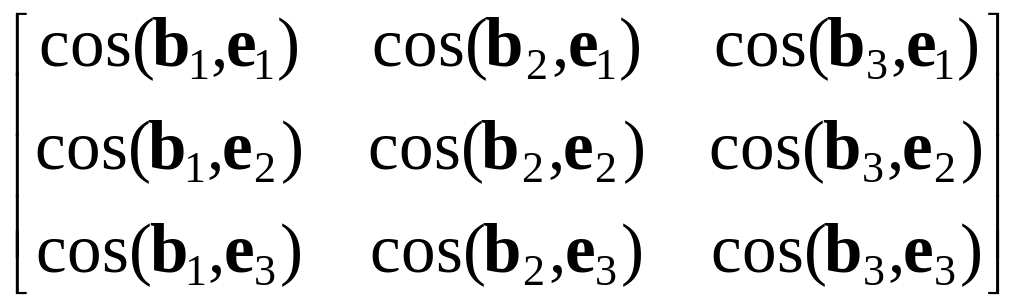
= +  . (1.22)

Перепишем формулу (1.22) в следующем виде:

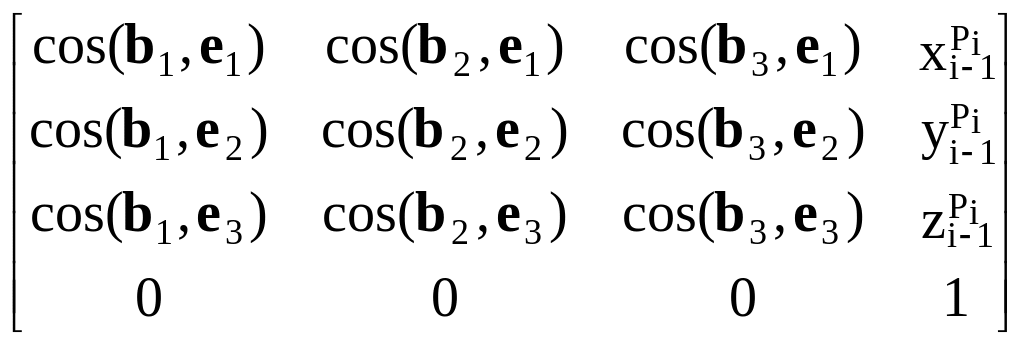
=  . (1.23)

Обозначим матрицу в (1.23) через T_i.

По формуле (1.23) можно вычислить координаты любой точки (а, следовательно, и всех точек) в (i–1)-й системе координат, если мы знаем координаты этой точки в i-й системе координат. Система P_ix_iy_iz_i движется произвольно. Матрица T_i содержит 6 неизвестных величин: , , и какие-то 3 из направляющих косинусов. Тем самым мы переоткрыли известный в механике факт, утверждающий, что положение твердого тела, произвольно перемещающегося в пространстве, определяется шестью величинами. При этом величины , , определяют положение (удаленность) тела относительно неподвижной системы координат, а косинусы углов определяют ориентацию тела относительно неподвижной системы координат. Заметим также, что формула (1.23) останется действительной и для того случая, когда точка А не принадлежит i-му телу. Достаточно лишь знать ее координаты в i-й системе и мы получаем возможность вычислить координаты этой точки в (i–1)-й системе.

Мы рассмотрели движение свободного тела, т. е. самый общий случай. В манипуляторе же тела связаны друг с другом. В следующей главе определим характер этих связей и то, как они повлияют на вид матрицы T_i в формуле (1.23).

1.5. Характер связей между звеньями

Договоримся, что звенья манипулятора будут соединяться в кинематические пары 5-го класса (практически все манипуляторы, используемые в промышленности, состоят из кинематических пар 5-го класса).

Как известно, кинематической парой 5-го класса называются два тела, связанные друг с другом и способные перемещаться друг относительно друга, но так, что положение одного тела относительно другого полностью описывается одним параметром – углом поворота или величиной линейного смещения (рис. 1.9).

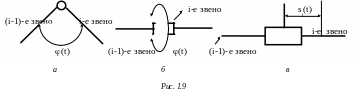
Кинематические пары 5-го класса бывают вращательными (рис. 1.9, а, б) и поступательными (рис. 1.9, в). Других пар 5-го класса не существует.

Во всех случаях (i–1)-е звено считаем неподвижным, а i-е звено – подвижным. Разумеется, за i-м звеном могут следовать и другие звенья, но в данном случае мы про них забываем.

Положение i-го звена относительно (i–1)-го полностью характеризуется в случае вращательной пары углом _i, в случае поступательной пары – линейным смещением s_i.

Если мы хотим получить описание того, как i-е звено движется относительно (i–1)-го в течение некоторого времени, то нужно составить соответствующую функцию – _i(t) (для вращательной пары) или s_i(t) (для поступательной пары).

Обратимся вновь к манипулятору. Для полного описания движения n-звенного манипулятора в пространстве нам необходимо знать n функций _i(t) и s_i(t), описывающих движение звеньев друг относительно друга.

Обозначим функции, характеризующие движение звеньев друг относительно друга, через q_i(t), i = 1,...,n. При этом будем иметь в виду, что q_i(t) = = _i(t), если пара вращательная, и q_i(t) = s_i(t), если пара поступательная. Функции q_i(t) называются обобщенными координатами манипулятора. Они объединяются в вектор обобщенных координат:

q(t) = 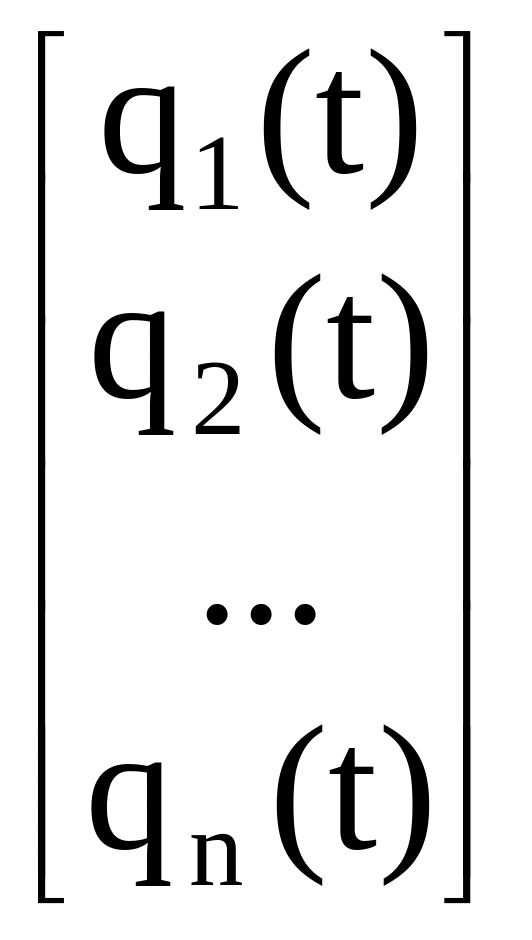. (1.24)

Пример. Вектор q(t) может иметь вид

q(t) = = 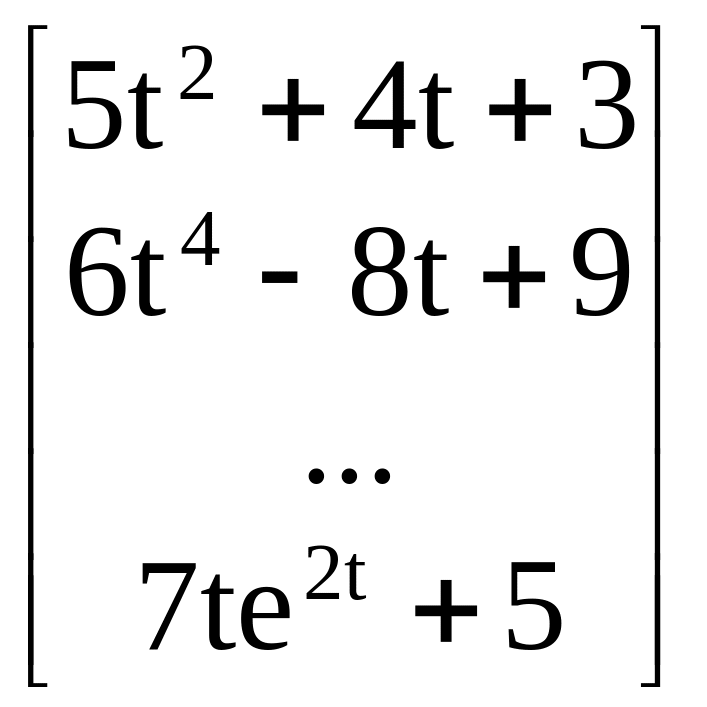. (1.25)

Вектор q(t) полностью описывает движение манипулятора в пространстве.