Правая часть (1.45), если k  j, k  I;

правая часть (1.46), если k  j;

правая часть (1.47), если k = j;

0, Если k  j.

Окончательно получаем

w₀^A = r_i^A +

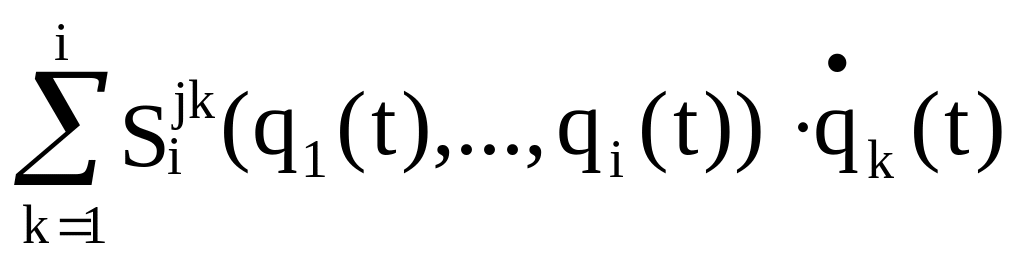+ ) r_i^A. (1.49)

Формула (1.43) позволяет вычислить скорость, а формула (1.49) – ускорение любой точки манипулятора.

1.10. Прямая задача кинематики

Прямая задача кинематики заключается в следующем: по известному вектору q(t) найти положение и ориентацию некоторого звена манипулятора (обычно схвата).

С одной стороны, звено представляет собой твердое тело, определенным образом расположенное в пространстве. Связь системы координат звена (пусть это i-е звено) и базовой системы координат согласно (1.23) находят по уравнению

= T_i . (1.50)

При выводе формулы (1.23) было указано, что величины , , определяют положение тела относительно неподвижной системы координат, а какие-то три из направляющих косинусов – ориентацию тела.

С другой стороны, звено принадлежит манипулятору и положение и ориентация звена обусловлены значениями обобщенных координат на данный момент времени. Связь системы i и базовой системы определяется уравнением кинематики (1.36) и имеет вид

= T₁ T₂ ... T_i = S_i . (1.51)

Матрица S_i есть матрица размером 44, все ее элементы известны.

Таким образом, если мы хотим знать положение звена, то из матрицы S_i надо взять величины , , . Если мы хотим знать ориентацию звена, то из матрицы S_i надо взять какие-то 3 косинуса (например, стоящие на месте элементов S_i¹³, S_i²³, S_i¹¹).

Математически эти действия можно записать следующим образом:

x = F(q(t)), (1.52)

x = ( , , )^T, (1.53)

F(q(t)) = (₁^TS_i(q(t)) ₄, ₂^TS_i(q(t)) ₄, ₃^TS_i(q(t)) ₄)^T, (1.54)

где ₁ = , ₂ = , ₃ = , ₄ = ; (1.55)

X = (q(t)); (1.56)

X = ( , , , S_i¹³, S_i²³, S_i¹¹)^T; (1.57)

(q(t)) = (F(q(t))^T, ₁^TS_i(q(t)) ₃, ₂^TS_i(q(t)) ₃, ₁^TS_i(q(t)) ₁)^T. (1.58)

По уравнению (1.56) можно решить прямую задачу кинематики.

1.11. Обратная задача кинематики

Обратная задача кинематики заключается в определении вектора обобщенных координат q(t) манипулятора с учетом известных положения и ориентации схвата X.

Запишем формулу (1.56) в виде шести уравнений:

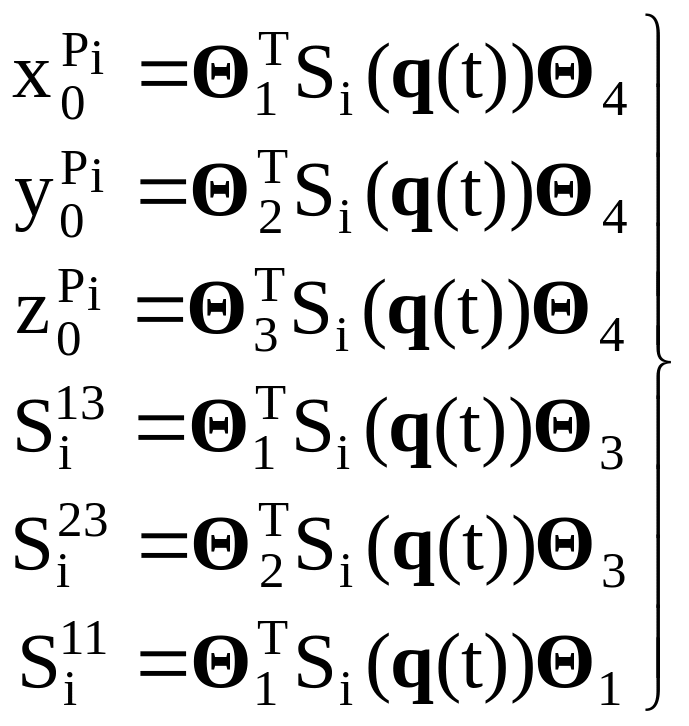. (1.59)

Величины, стоящие в (1.59) слева, известны. Для нахождения обобщенных координат необходимо решить систему из 6 нелинейных уравнений (1.59) с n неизвестными. Аналитическое решение системы (1.59) возможно, но не всегда. Дело осложняется тем, что решение системы (1.59) может быть не единственным. Этот факт можно продемонстрировать на следующем примере (рис. 1.19).

Для заданного положения X схвата возможны две конфигурации:

q^I = (q₁^I,q₂^I)^T, q^II = (q₁^II,q₂^II)^T.

Для решения системы (1.59) могут быть применены численные методы. Для этого сначала приведем (1.59) к виду (1.60) путем переноса правых частей (1.59) в левые.

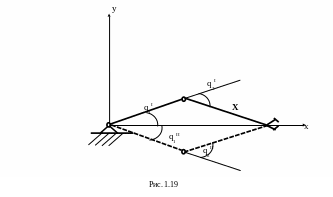
Система (1.60) будет решена, если мы найдем такой вектор q, который, будучи подставлен в (1.60), обращает все уравнения в тождества:

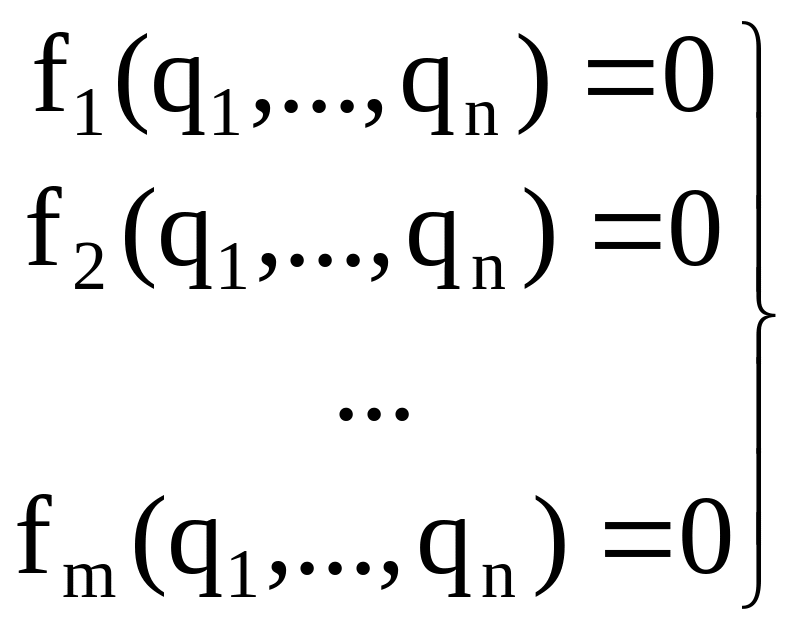. (1.60)

Задача нахождения вектора q может быть сформулирована следующим образом. Составим функцию

f(q₁,...,q_n) = f₁²(q₁,...,q_n) + f₂²(q₁,...,q_n) + ... + f_m²(q₁,...,q_n). (1.61)

Поставим себе задачу: найти такой вектор q, который, будучи подставлен в функции f₁, f₂, ..., f_m, обращает каждую из них в нуль и тем самым обращает в нуль и функцию f. Поскольку функция f может принимать значения только большие или равные нулю, то вектор q, при котором f становится равной нулю, одновременно является и тем вектором, при котором f принимает минимальное значение. То есть, найдя такой вектор, мы тем самым найдем решение системы.

Одним из методов поиска минимума функции является метод градиентного спуска. При использовании этого метода поиск минимума функции f(q₁,...,q_n) осуществляется с помощью такой последовательности итераций:

q^k+1 = q^k - agradf(q₁^k,...,q_n^k), (1.62)

где a – весовой коэффициент (величина шага).

Схема поиска минимума функции состоит в следующем: задаем произвольное значение q⁰, подставляем его в (1.61) и вычисляем f(q⁰). Так как мы знаем, что минимальное значение функции равно 0, то проверяем, равно ли нулю f(q⁰). Если f(q⁰) = 0, то q⁰ является решением системы, если же f(q⁰) ≠ 0, то по формуле (1.62) вычисляем q¹ и повторяем итерационный процесс.

Формула (1.63) представляет собой покоординатную запись уравнения (1.62):

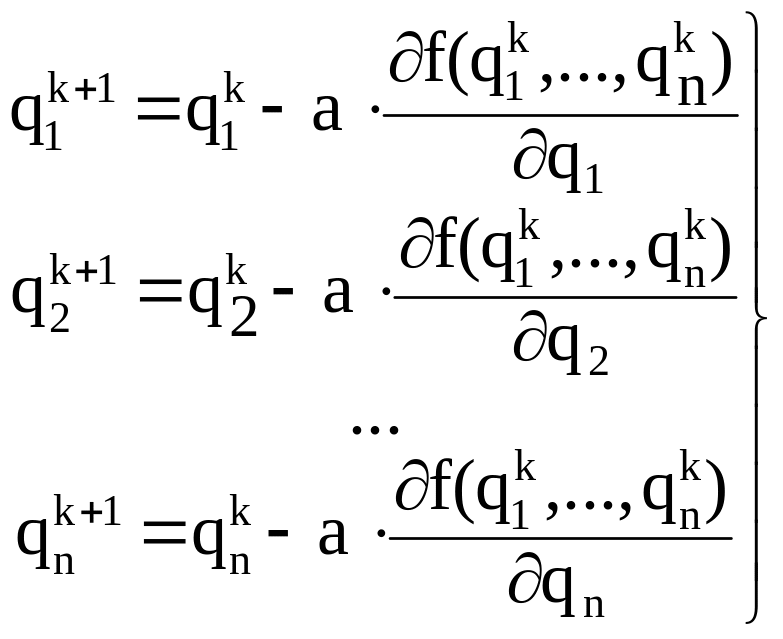. (1.63)

Итак, приведя систему (1.59) к виду (1.60) и используя методы поиска минимума функции, можно численно решать обратную задачу кинематики.

В этой главе мы нашли способ описания движения манипуляторов – с помощью вектора обобщенных координат q(t). Если мы имеем этот вектор, то, решив прямую задачу кинематики, можем получить формулы, описывающие движение любой точки манипулятора в базовой системе координат (а следовательно, и всех точек). Для этого, как мы видели, необходимо знать координаты этой точки в системе координат того звена, которому данная точка принадлежит. Кроме того был предложен способ решения обратной задачи кинематики – определение вектора q(t) исходя из положения и ориентации схвата.