Библиографический список

1. Моисеев, Н. Н. Элементы теории оптимальных систем [Текст] / Н. Н. Моисеев. – М.: Наука, 1975. – 526 с.

2. Понтрягин, Л. С. Принцип максимума в оптимальном управлении [Текст] / Л. С. Понтрягин. – М.: Наука, 1989. – 60 с.

3.5. Исполнение траектории

Предположим, что мы нашли траекторию q(t), которую манипулятор должен исполнить, и управляющие силы Q(t), которые двигатели должны приложить к звеньям, чтобы они отработали требуемую траекторию. По уравнению привода можно вычислить токи, подаваемые на двигатели. То есть мы могли бы действовать в соответствии со схемой (см. рис. 2). Однако вследствие того, что уравнения динамики и привода лишь приближенно описывают реальные процессы, происходящие в манипуляторе, и звенья в процессе движения подвергаются различного рода возмущающим воздействиям, в действительности мы получим, что реальная траектория q_р(t) не будет равна желаемой q_ж(t). Но нам необходимо, чтобы q_р(t)  q_ж(t), или, в других обозначениях,

e(t) = q_ж(t) – q_р(t)  0, (3.92)

где e(t) – рассогласование между q_ж(t) и q_р(t).

Следовательно, нам надо построить такую управляющую систему (регулятор), чтобы она обеспечивала e(t)  0.

Опишем одну идею [1], позволяющую рассчитать управляющие токи так, чтобы ошибка в исполнении желаемой траектории стремилась к нулю. Будем считать, что привод описывается уравнением:

_p(t) = D_{1 p}(t) + D₂u_p(t) + D₃M_н(q_р(t), _р(t), c), (3.93)

где D_j – diag(d_1j, ..., d_nj) – диагональные матрицы размерности n × n, элементы которых выражаются через параметры приводов; M_н(q(t), (t), c) – n-мерный вектор нагрузок на выходных валах приводов, определяемый согласно формуле (5.2) [1]; u(t) – n-мерный вектор обобщенных сил, развиваемых приводами.

Уравнение (3.93) описывает определенный класс приводов с двигателями постоянного тока с независимым возбуждением [1].

Уравнение динамики манипулятора (2.50) запишем в скорректированном виде [1]:

Â(q_p(t), c) _р(t) +ß(q_p(t), _р(t), c) = u_p(t). (3.93а)

Здесь

Â(q_p(t), c)= A(q_p(t), c)+J_1д,

где J_1д – диагональная матрица моментов инерции (масс) перемещающихся частей (роторов) двигателей, умноженных на квадраты передаточных отношений, ß(q_p(t), _р(t), c)= b(q_p(t), _p(t), c)-M_T-M_В, где M_T и M_В – векторы моментов сопротивления, создаваемых силами трения, и внешних моментов на валах нагрузки (см. формулу (5.2) [1]).

Будем подавать на привод v_р(t) такое, что

_p(t) = D_{1 p}(t) + D₂{ Â(q_p(t), c)[ _ж(t) + Г₁( _p(t) – _ж(t)) +

+ Г₀(q_p(t) – q_ж(t))] + ß(q_p(t), _p(t), c)} + D₃M_н(q_p(t), _p(t), c), (3.94)

где Г₀ = diag(₁₀, ..., _n0), Г₁ = diag(₁₁, ..., _n1) – диагональные матрицы размерности n x n, _ij < 0, i=1,...,n, j=0,1.

Вектор v(t) можно вычислить из (3.94) по известной формуле

v(t) = v(t₀) + (t)dt. (3.95)

Покажем, что если мы хотим исполнить траекторию q_ж(t) и будем подавать на приводы токи v(t), вычисленные по формулам (3.94) и (3.95), то e(t)  0.

Подставим правую часть (3.94) в левую часть (3.93), получим

D_{1 p}(t) + D₂{ Â(q_p(t), c)[ _ж(t) + Г₁( _p(t) – _ж(t)) +

+ Г₀(q_p(t) – q_ж(t))] + ß(q_p(t), _p(t), c)} + D₃M_н(q_p(t), _p(t), c) =

= D_{1 р}(t) + D₂u_р(t) + D₃M_н(q_р(t), _р(t), c). (3.96)

После сокращений

Â(q_p(t), c)[ _ж(t) + Г₁( _p(t) – _ж(t)) +

+ Г₀(q_p(t) – q_ж(t))] + ß(q_p(t), _р(t), c) = u_p(t). (3.97)

В правую часть (3.97) подставим левую часть (3.93а), получим

Â(q_p(t), c)[ _ж(t) + Г₁( _p(t) – _ж(t)) +

+ Г₀(q_p(t) – q_ж(t))] + ß(q_p(t), _р(t), c) = Â(q_p(t), c) _р(t) +

+ ß(q_p(t), _р(t), c). (3.98)

После сокращений получаем

( _ж(t) – _р(t)) + Г₁( _p(t) – _ж(t)) + Г₀(q_p(t) – q_ж(t)) = 0, (3.99)

или

(t) – Г₁ (t) – Г₀e(t) = 0. (3.100)

Уравнение (3.100) для i-й обобщенной координаты имеет вид

_i(t) – _{i1 i}(t) – _i0e_i(t) = 0, i=1,…,n. (3.101)

Как известно, для уравнения (3.101) можно записать характеристическое уравнение в виде

² – _i1 – _i0 = 0. (3.102)

Если характеристическое уравнение имеет простые корни _1i и _2i, то решение уравнения (3.101) имеет вид

e_i(t) = , (3.103)

если же характеристическое уравнение имеет кратный корень _0i, то решение уравнения (3.101) имеет вид

e_i(t) = , (3.104)

Можно показать, что если _i1, _i0 отрицательны, то корни уравнения (3.102) также будут отрицательны, а значит, с течением времени e_i(t)  0, что нам и требуется. Постоянные c_1i и c_2i определить можно, так как известны e_i(t₀) и _i(t₀), i=1,2,…,n.

Итак, мы показали, что если на приводы подавать токи v(t), вычисляемые согласно формулам (3.94) и (3.95), то e(t)  0 и q_р(t)  q_ж(t).

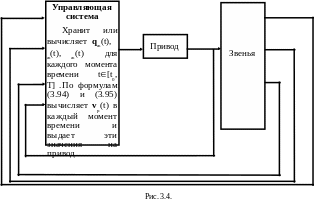
В связи с этим изменится схема управления манипуляторами. Во введении (см. рис. 2) мы дали схему управления манипуляторами, которая называется «схемой без обратной связи». Такая схема не способна корректировать исполняемую траекторию, ее надо изменить. Мы видим, что при вычислении управляющих токов по формуле (3.94) необходимо знать как желаемые траекторию, скорость и ускорение, так и действительные их значения, а также действительные значения управляющих сил, прилагаемых двигателями к звеньям. Эти значения будут подаваться в управляющую систему через датчики обратной связи (рис. 3.4). Такая схема называется схемой управления манипуляторами с обратной связью.

В данной главе мы рассмотрели способ исполнения траектории для определенного класса электроприводов. Более подробный и углубленный анализ вопросов исполнения траектории приведен в [1, 2].

q(t) q_p(t)

(t) v_p(t) u_p(t) (t)

(t) (t)

u_p(t)