2.4. Уравнение динамики манипулятора
Теперь мы готовы к тому, чтобы, подставив выражения (2.19) и (2.26) в систему уравнений (2.1), получить уравнение динамики манипулятора.
Распишем выражение для кинетической энергии (2.19) более подробно:
K
=
=
=
=
=
+
+
+...+
+
)=
=
+
+
+
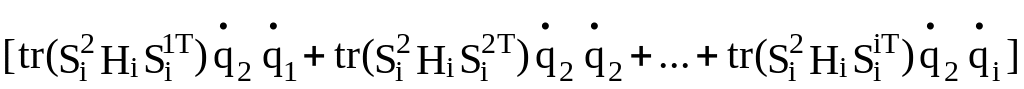(2.27)
+
+
+
+
+
+
+
+
+
+
+
}+...+
+
+
+
+
+...+
+...+
+
+
+...+
}.
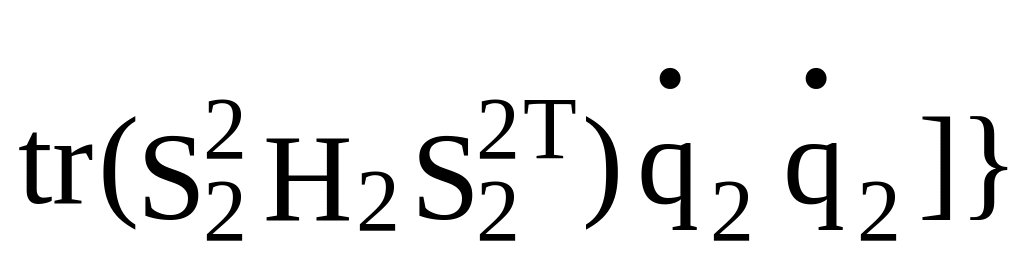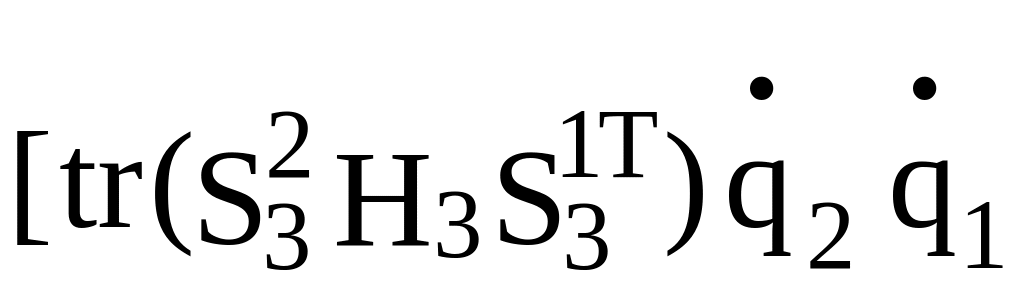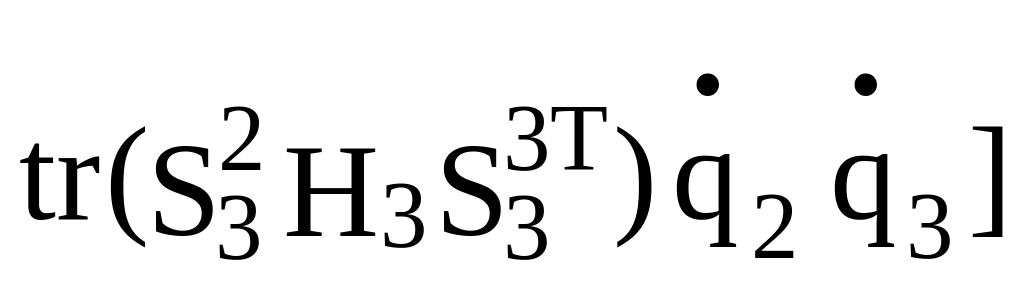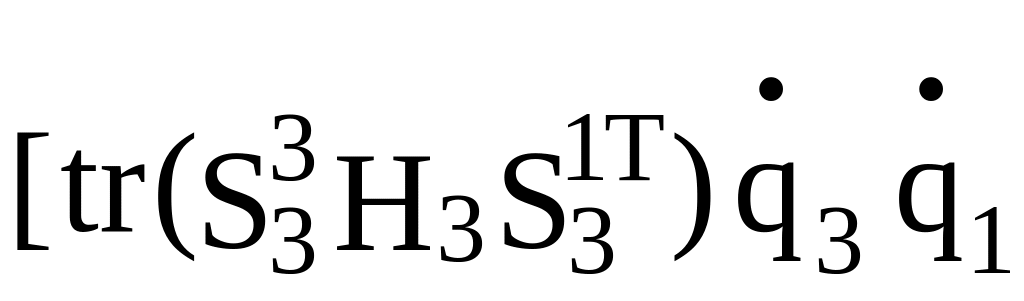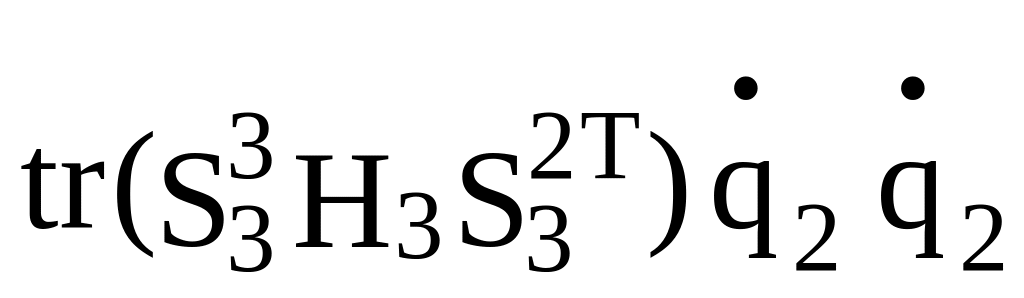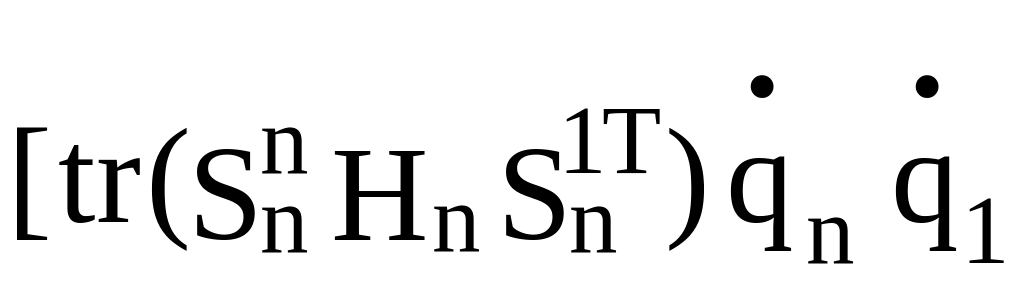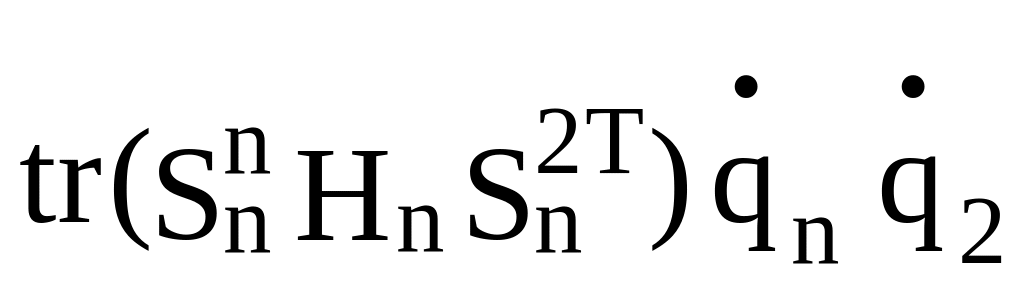Вычислим
=
=
=
=
=
| учтем,
что tr(AHST)
= tr(SHAT)
и что
=
0 при k>i |
=
=
=
(2.28)
При
вычислении
будем учитывать, что обобщенные скорости
не входят в матрицы
и Hi.
На то, что в формуле (2.29) одни слагаемые
написаны курсивом, а другие – обычным
шрифтом, пока не обращаем внимания:
=
+
}
+
+
+
+
+
+
+
+
+
+...+
+
+
+
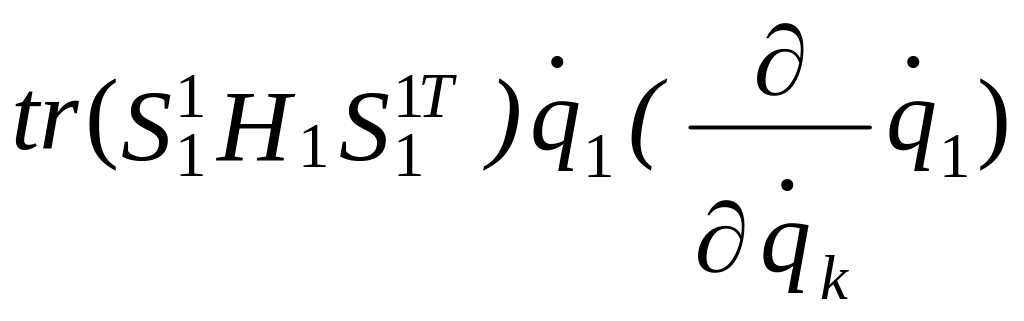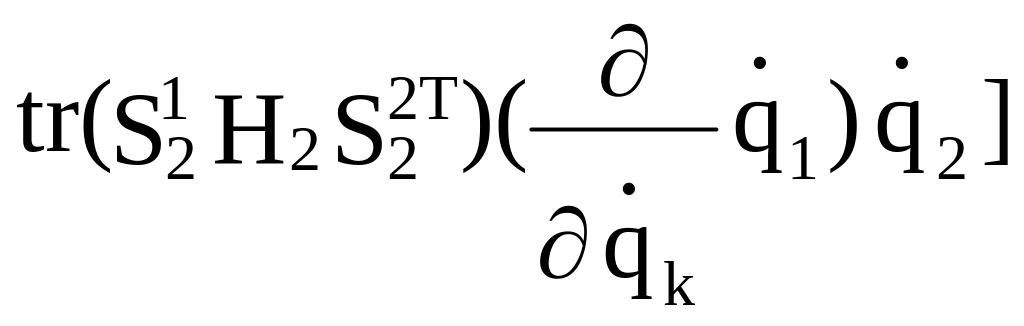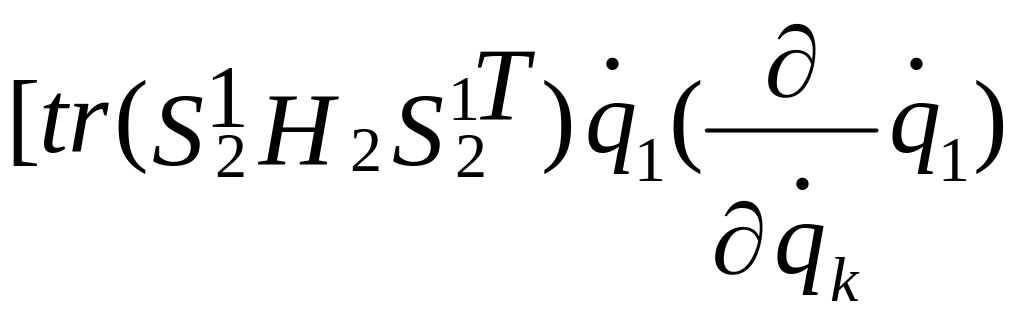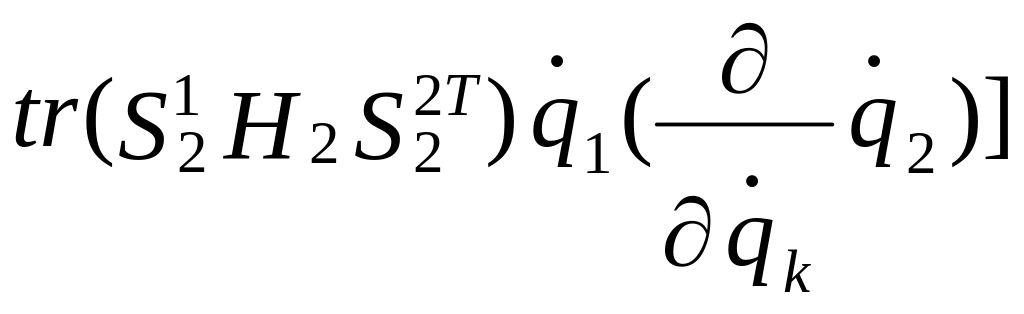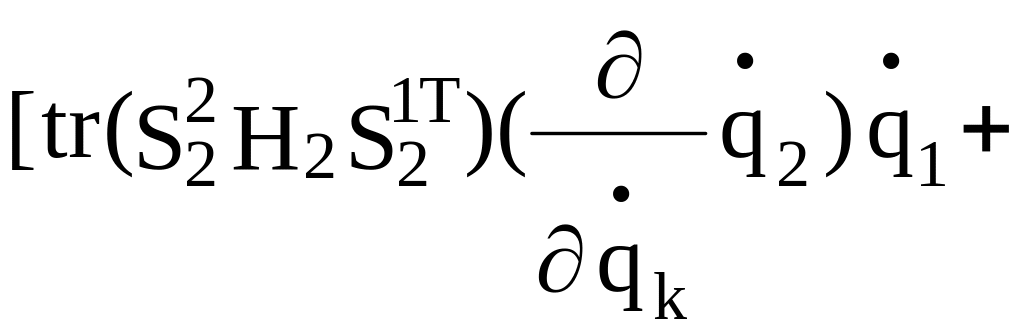
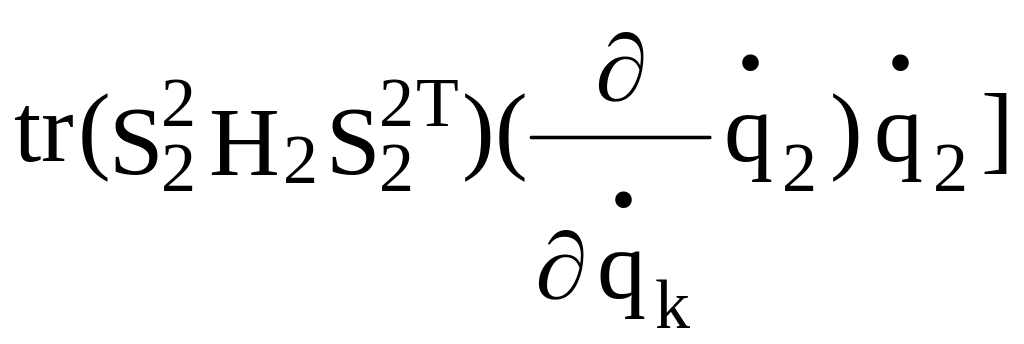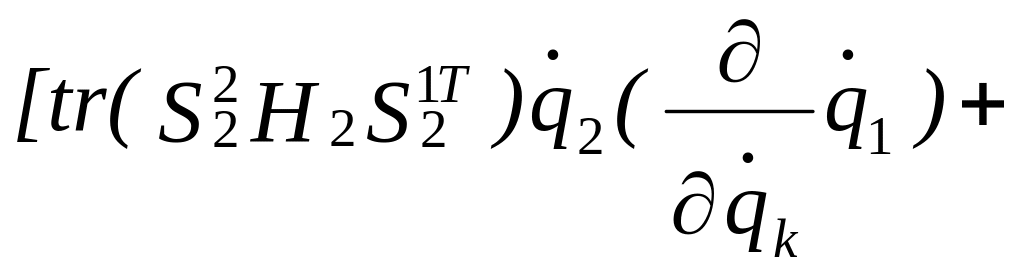
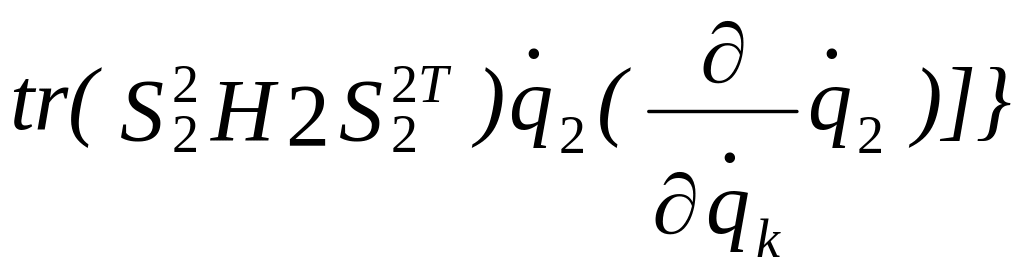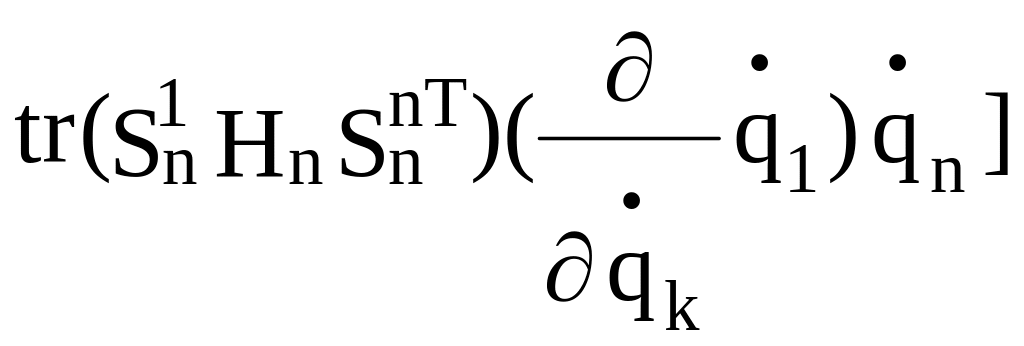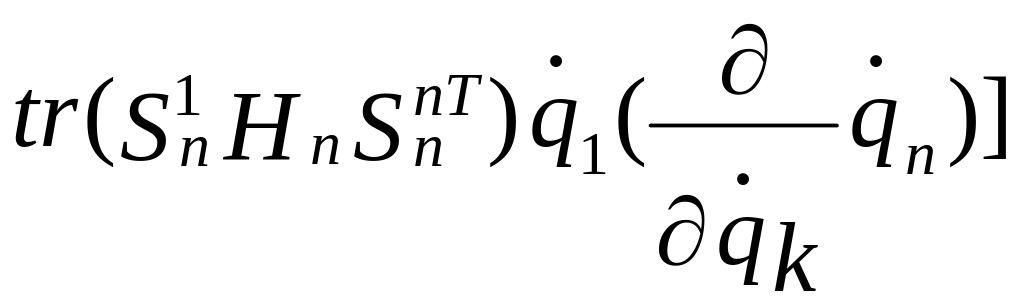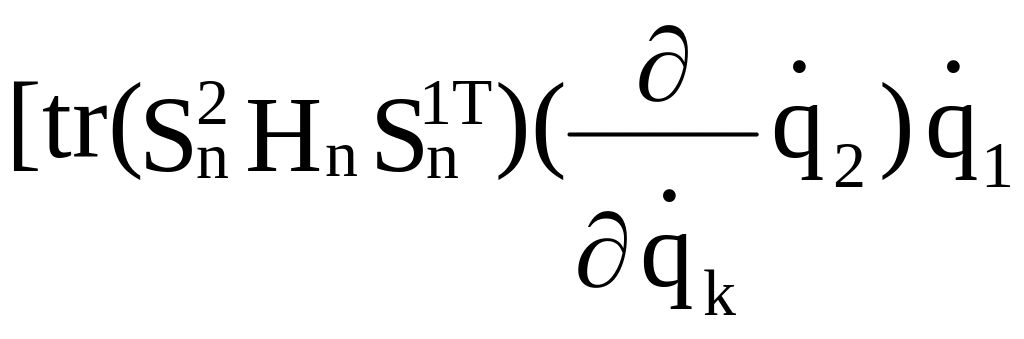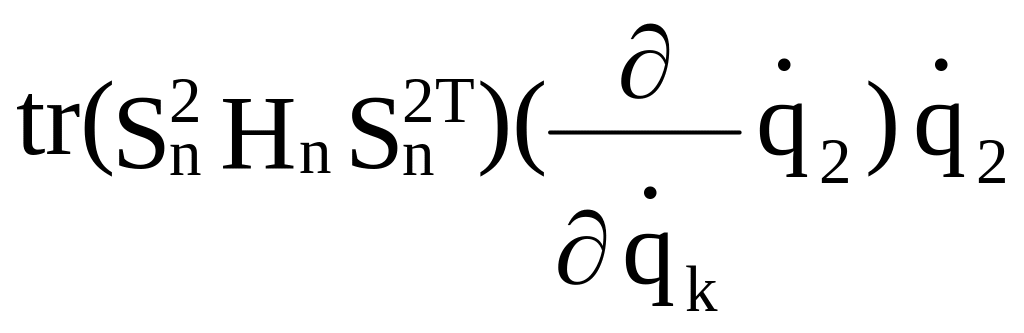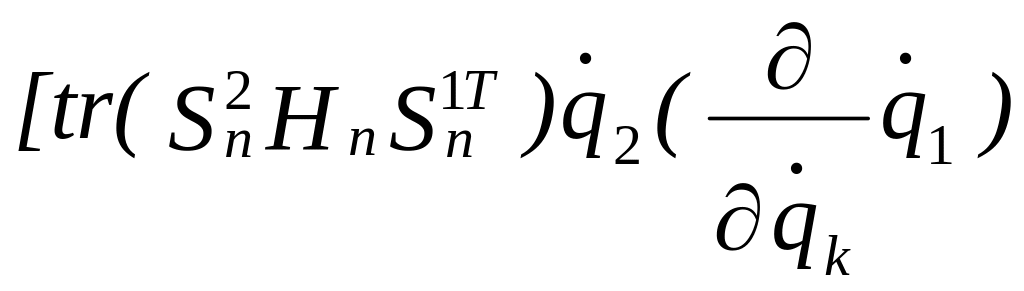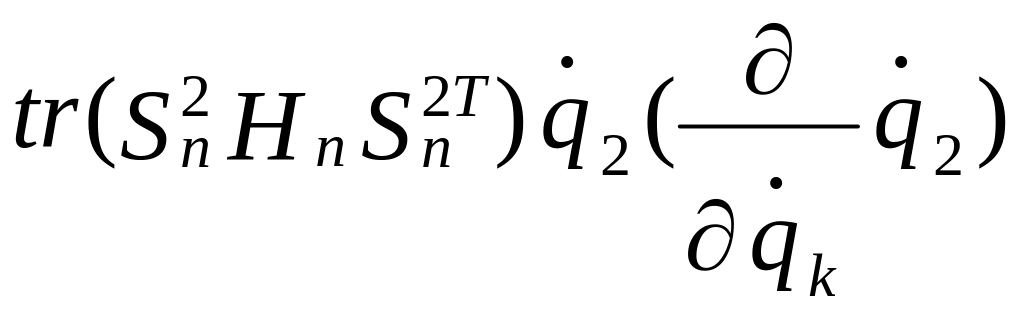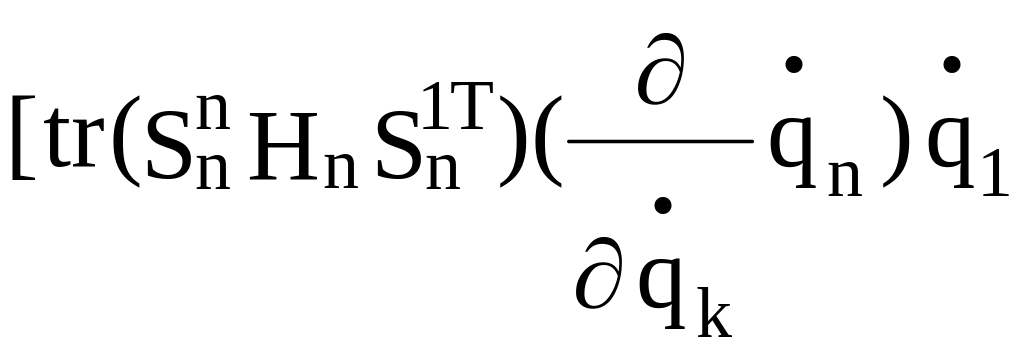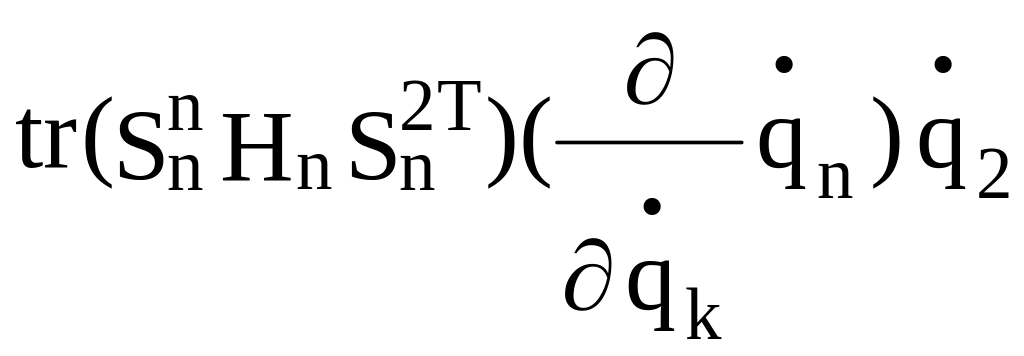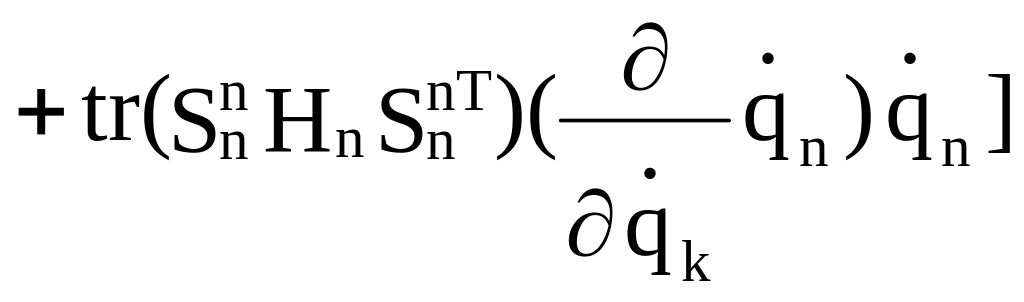(2.29)
+
+
+
+
+...+
+
+
+
+...+
+....+
+
+
+...+
+
(2.29)
+
+
+...+
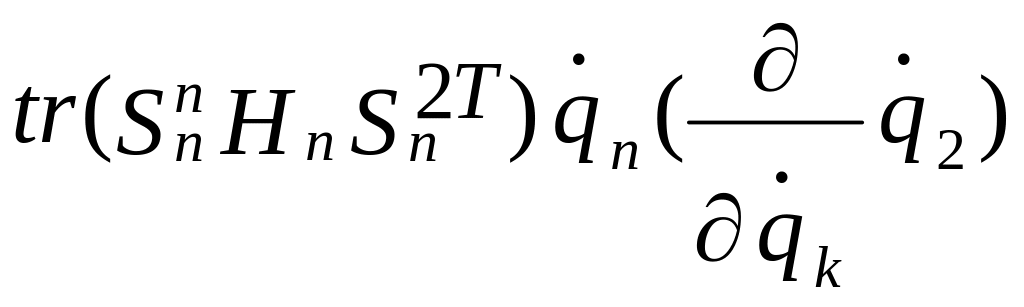Обращаем внимание, что если k = 1, то при дифференцировании остаются все фигурные скобки. Если k = 2, исчезает первая фигурная скобка и т.д. Если k = n, то исчезают все фигурные скобки, кроме последней. Если k совпадает с индексом обобщенной скорости, которую мы собираемся дифференцировать, то после дифференцирования останется 1, если не совпадает – останется 0.
Выпишем в формуле (2.29) члены, написанные не курсивом:
A
=
}
+
+
+
+
+
}+...+
+
+
+
+
+
+...+
+
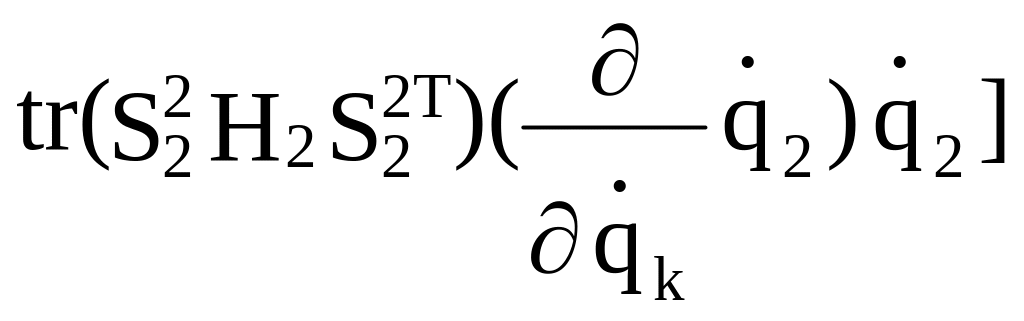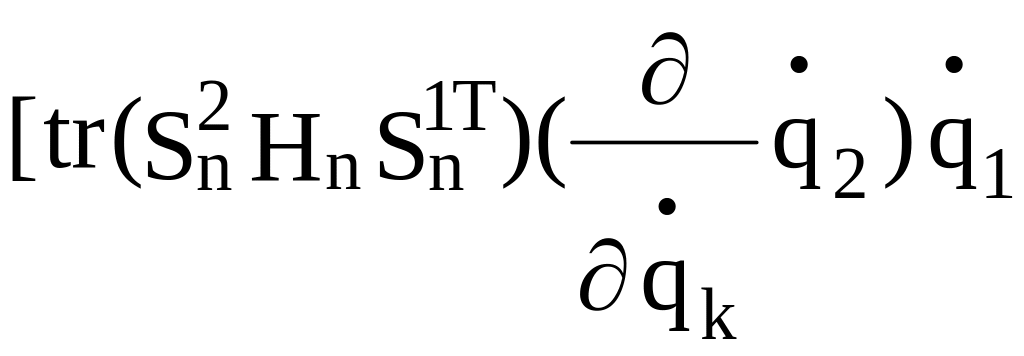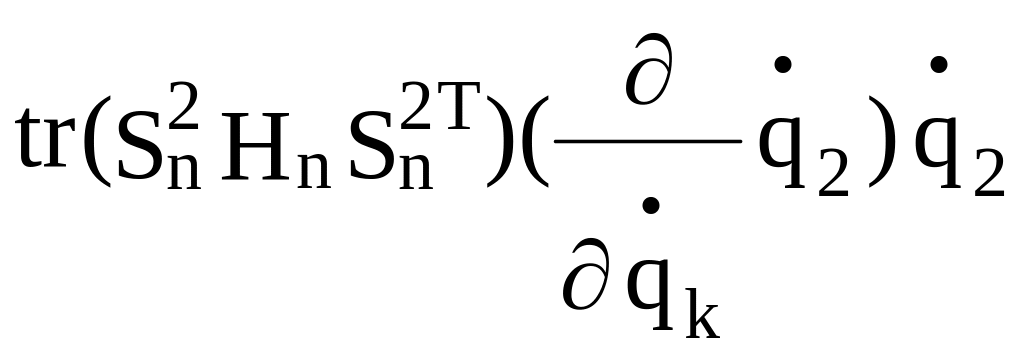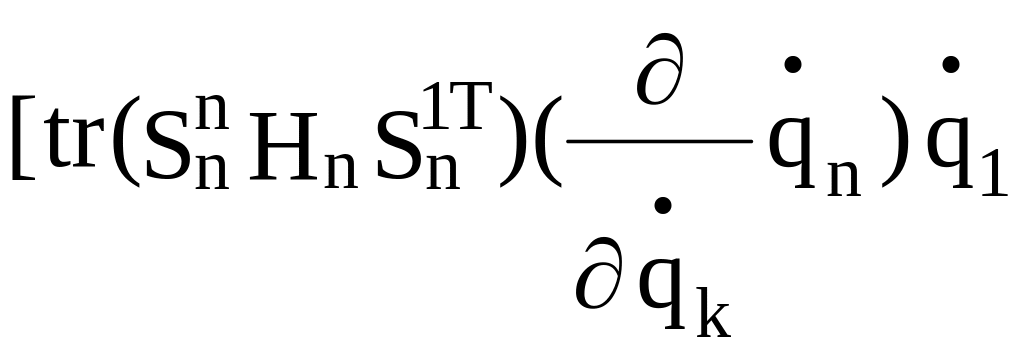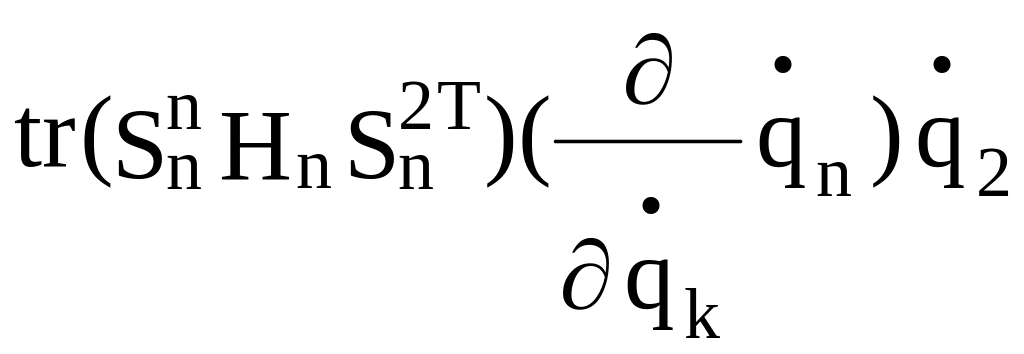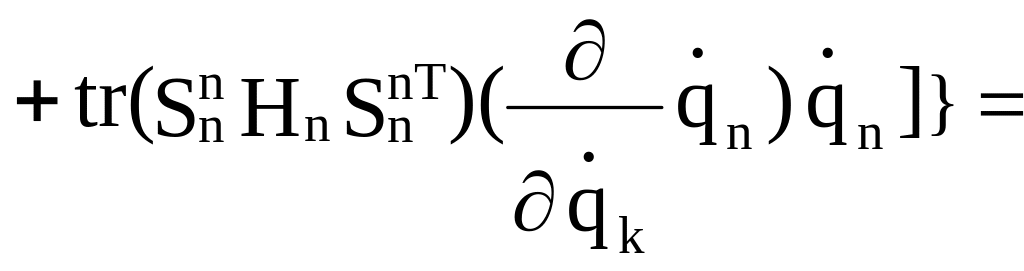
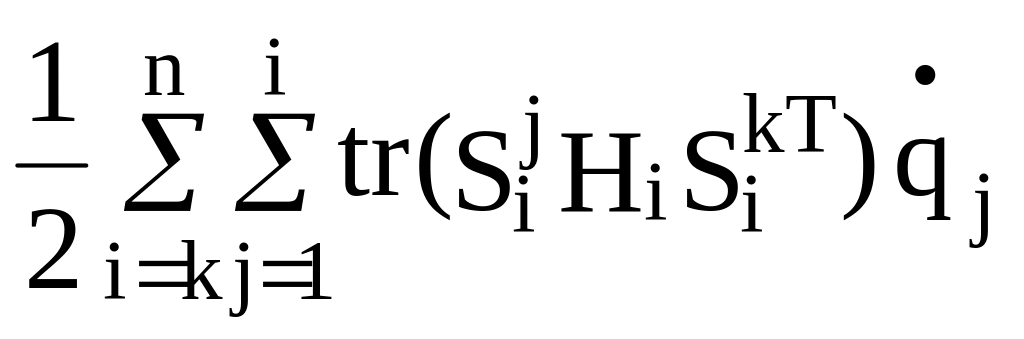(2.30)
+....+
+
+
+...+
=
.
(2.30)
Можно видеть, что члены формулы (2.29), написанные курсивом, равны соответствующим членам, написанным не курсивом. Поэтому
=
.
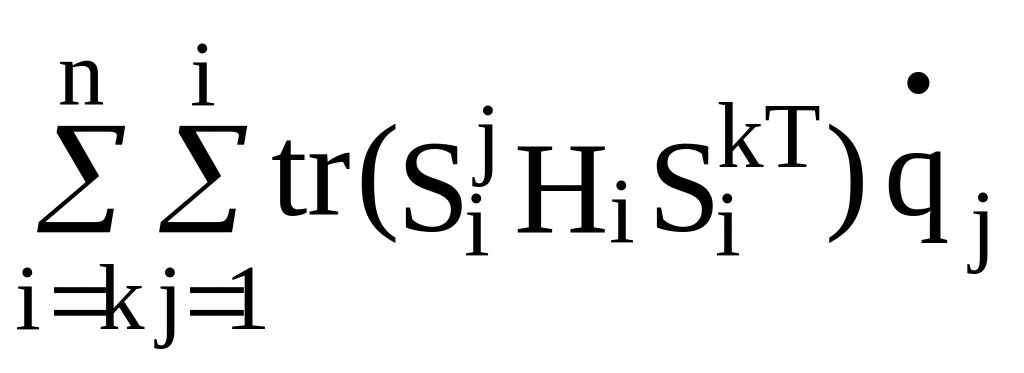(2.31)
Вычислим
:
=
=
=
=
+
=
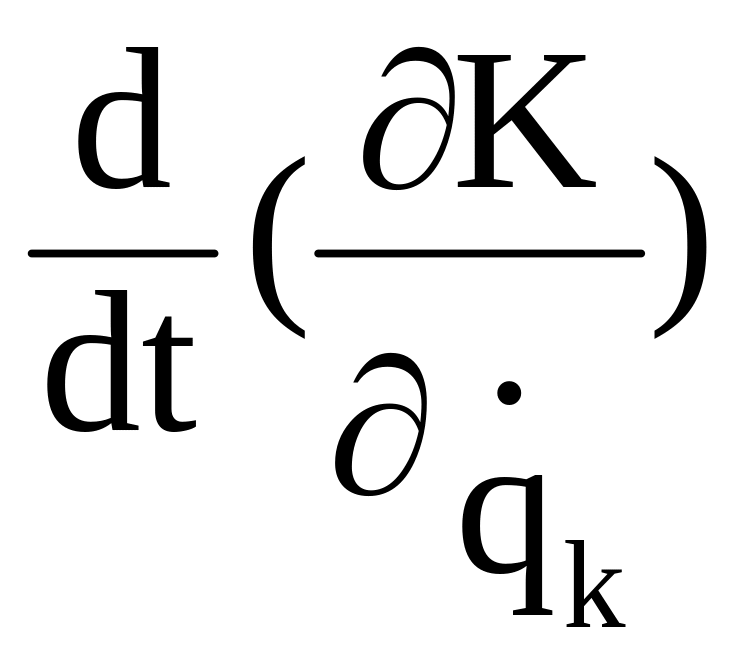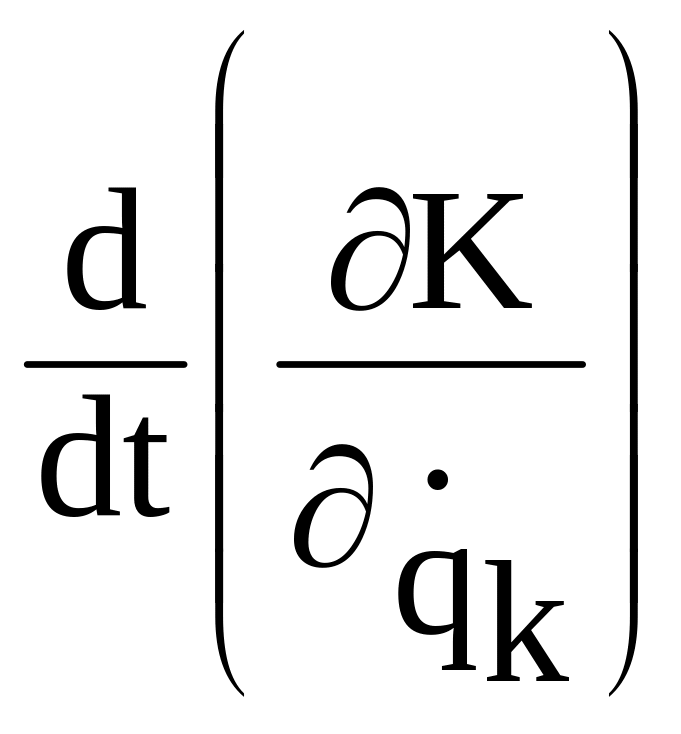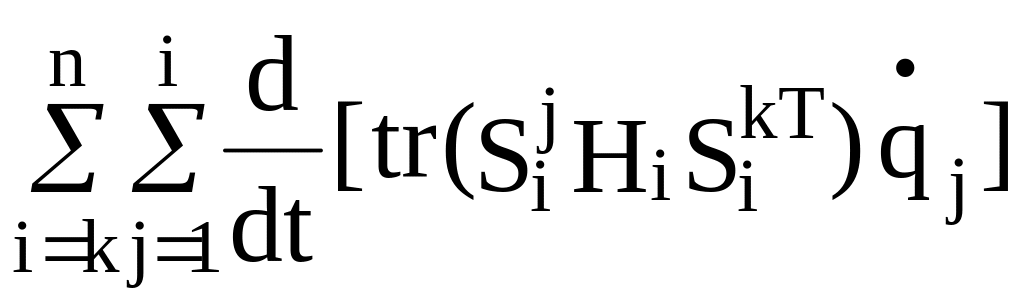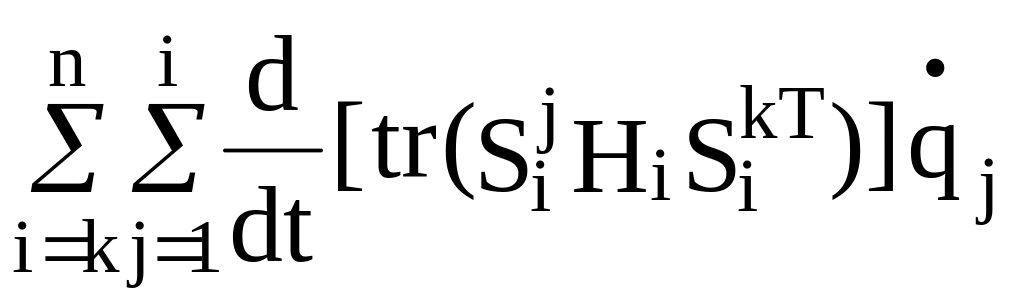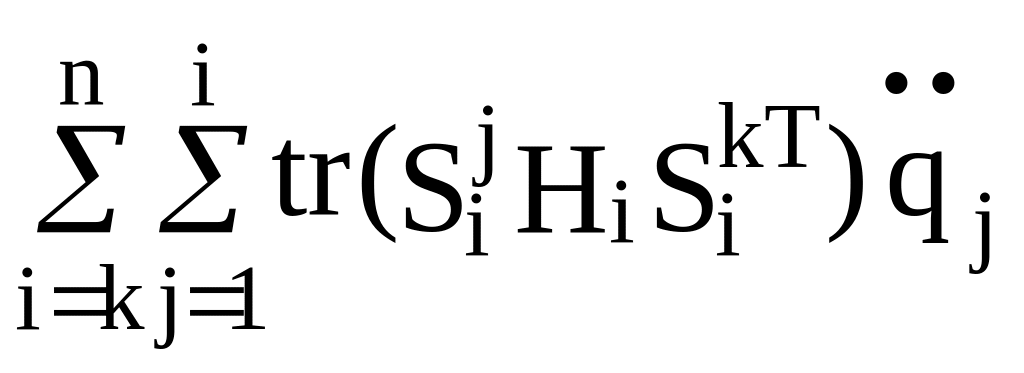(2.32)
=
+
=
=
+
.
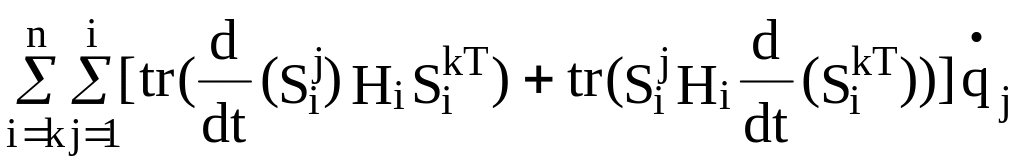Можно также видеть, что
=
0 , k=1, ... , n (2.33)
и
=
.
(2.34)
Таким образом, уравнение динамики манипулятора принимает вид
+
–
–
+
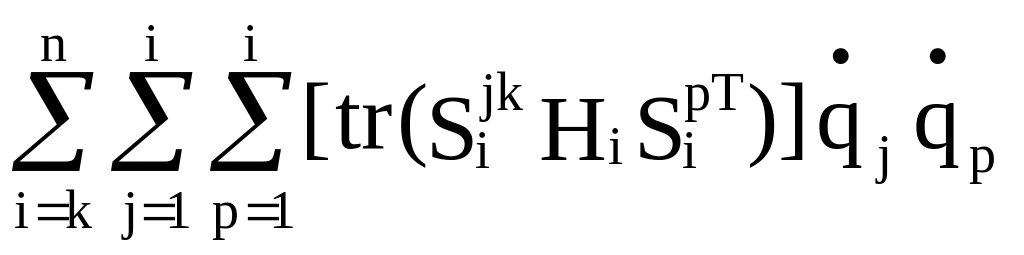=Qk,
k=1,2,...,n.
(2.35)
Введем обозначения:
=
,
(2.36)
=
(
,
(2.37)
,
(2.38)
,
(2.39)
ak(q,
c)
=
,
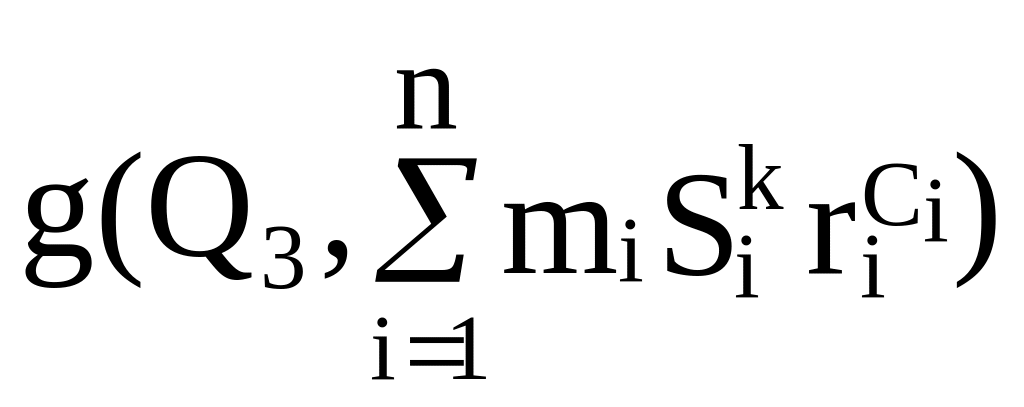(2.40)
где с – вектор параметров манипулятора (длины звеньев, масса и моменты инерции звеньев и т.д.).
Теперь уравнение динамики манипулятора принимает вид
,
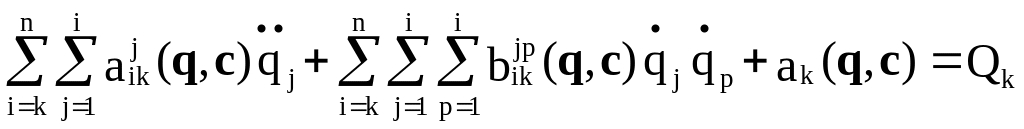k=1,...,n. (2.41)
Преобразуем первое слагаемое в (2.41):
=
=
=
+
+...+
+
=
=
+
+...+
+
+...+
=
=
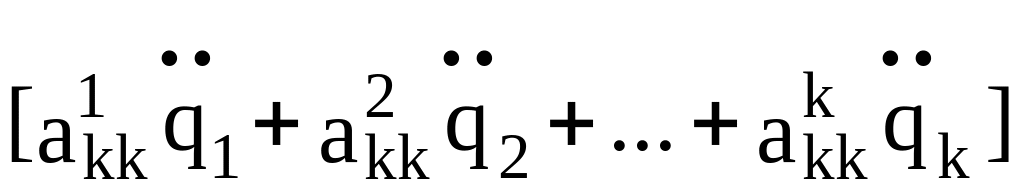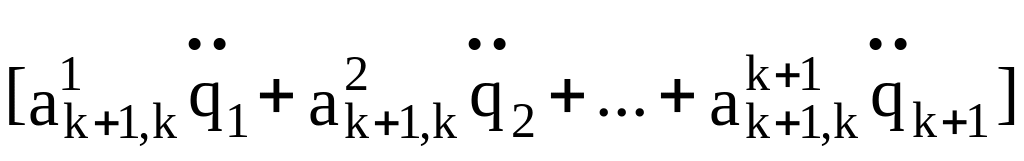=|обозначим
|=
.
(2.42)
Аналогично преобразуем второе слагаемое в (2.41):
=
=
,
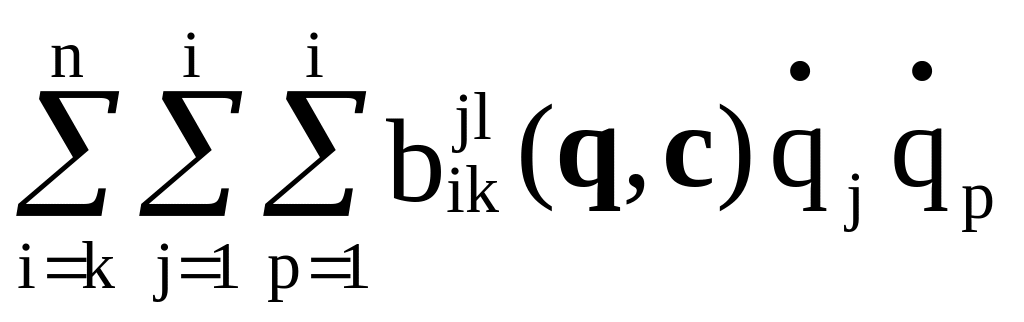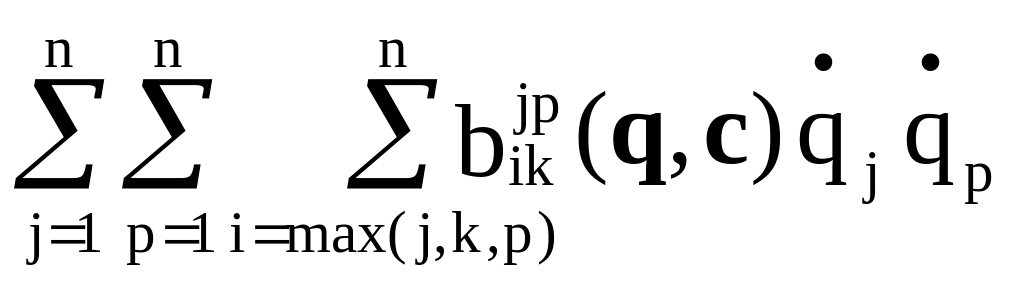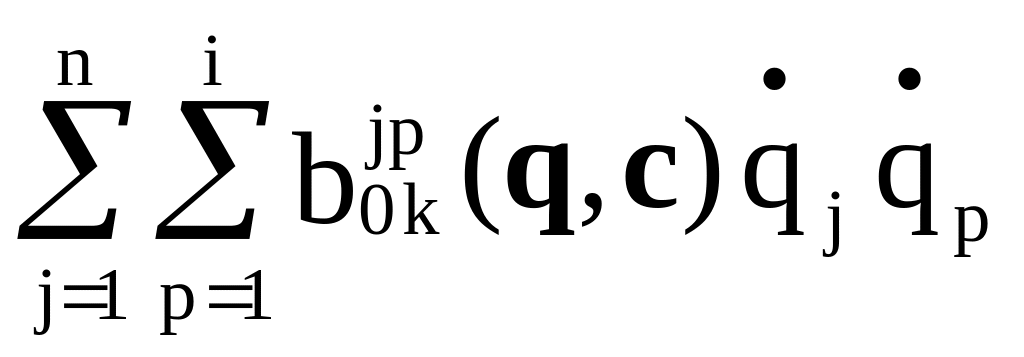(2.43)
где
=
.
(2.44)
Тогда уравнение динамики манипулятора принимает вид
+
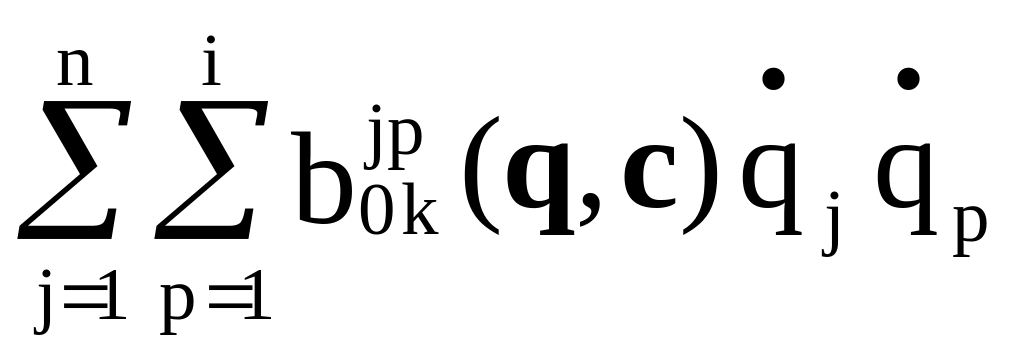+ ak(q,
c)
= Qk,
k=1,...,n,
(2.45)
или построчно
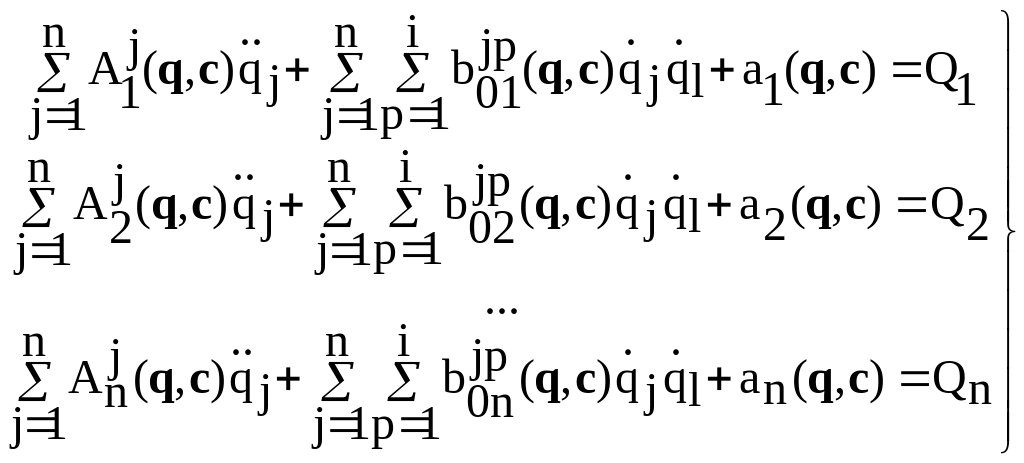
. (2.46)
Введем обозначения:
A
=
,
(2.47)
b(q,
,c)
=
=
,
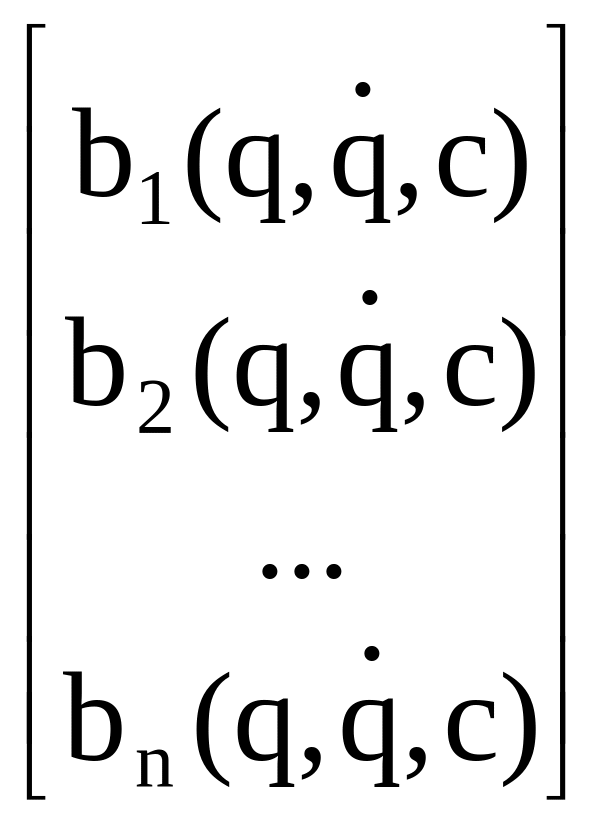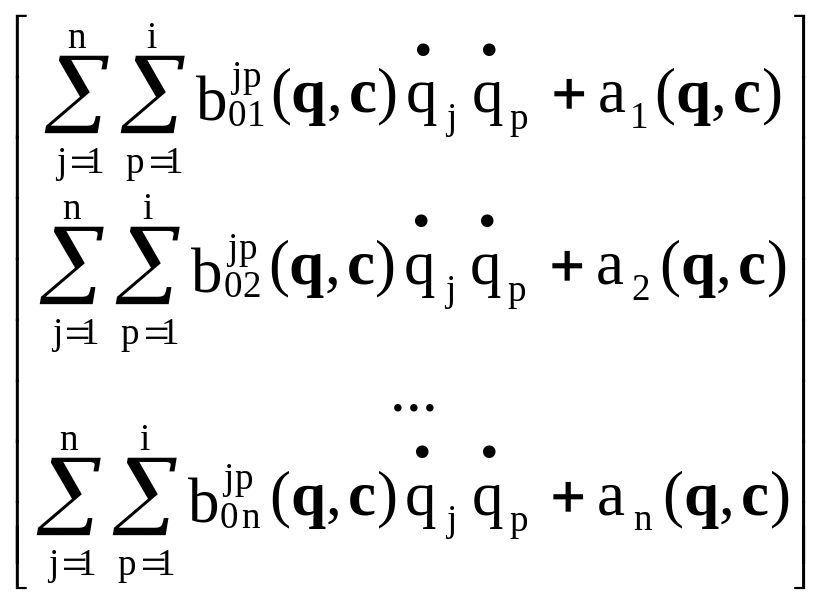(2.48)
Q
=
.
(2.49)
Принимая во внимание обозначения (2.47)–(2.49), мы можем записать уравнение динамики манипулятора следующим образом:
A(q(t),
c)
(t) + b(q(t),
(t), c)
= Q(t).
(2.50)
Запись (2.50) является общепринятой обобщенной формой записи уравнения динамики манипуляторов. Уравнение динамики устанавливает зависимость между вектором обобщенных координат q(t) и вектором обобщенных сил Q(t).
Мы вывели систему уравнений (2.50), называемых в робототехнике «уравнением динамики манипулятора». Если мы знаем, как изменяется (или как должен изменяться) вектор q(t), то по уравнению динамики можно узнать, как должны изменяться обобщенные силы Q(t), чтобы манипулятор отработал траекторию q(t). И наоборот, если мы знаем, как изменяется вектор Q(t), то, дважды проинтегрировав систему (2.50), можно вычислить q(t). Вычисление Q(t) по известному q(t) называется прямой задачей динамики, а вычисление q(t) по известному Q(t) называется обратной задачей динамики.