Разделим уравнение (1.71) на (1.72). Получим

. (1.77)

Отсюда

q₁ = 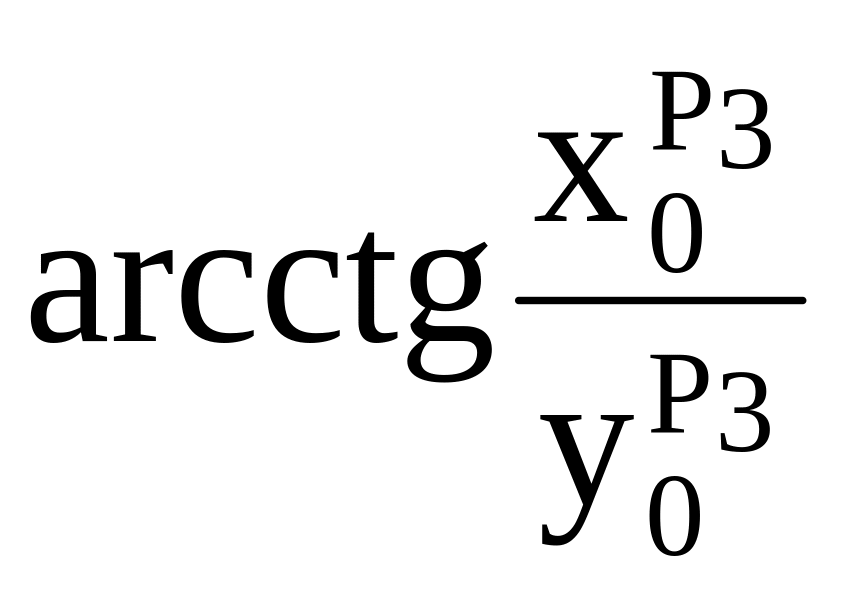. (1.78)

Уравнение (1.73) преобразуем к виду

( – l₁) = (l₂ + q₃) cos q₂. (1.79)

Разделим уравнение (1.72) на (1.79). Получим

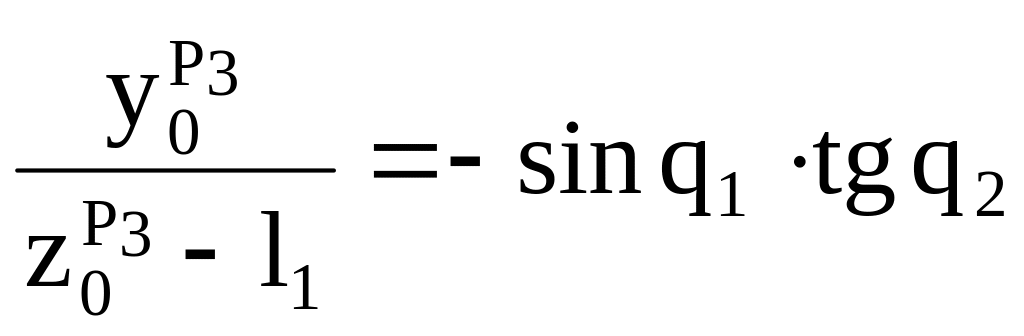. (1.80)

Отсюда получим

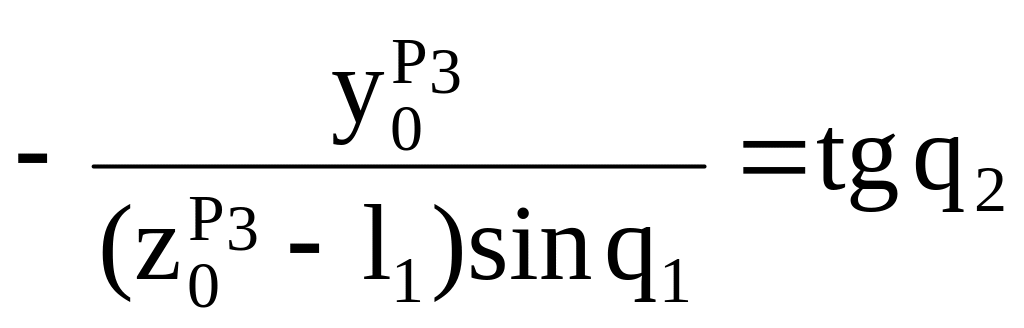. (1.81)

Подставляя в (1.81) соотношение (1.78), получим

q₂ = arctg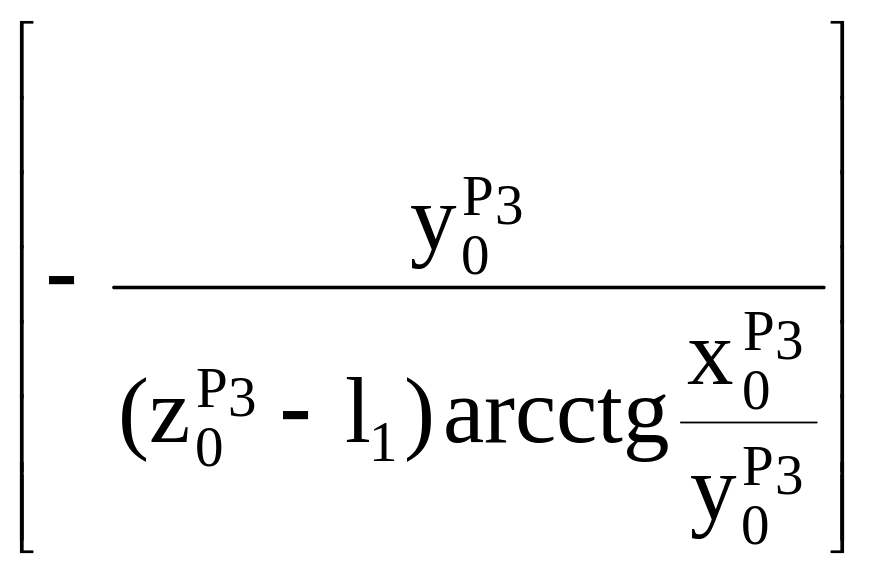 . (1.82)

Из уравнения (1.73) получаем значение

q₃ = , (1.83)

где q₂ подсчитывается по формуле (1.82).

Задачи для самостоятельного решения

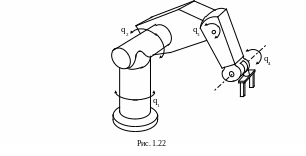
1. Расставьте системы координат, связав их со звеньями манипулятора (рис. 1.22) в соответствии с алгоритмом Денавита-Хартенберга. Получите матрицы перехода T_i (i=1,2,3) от i-й к (i-1)-й системе координат.

2. Решите прямую задачу кинематики для манипулятора, изображенного на рис. 1.22.

3. Решите обратную задачу кинематики для манипулятора, изображенного на рис. 1.22.

Библиографический список

1. Вукобратович, М. Шагающие роботы и антропоморфные механизмы [Текст] / М. Вукобратович. – М.: Мир, 1976. – 541с.

2. Denavit, J. A Kinematic Notation for Lower-Pair Mechanisms Based on Matrices [Text] / J. Denavit, R. S. Hartenberg // ASME J. Appl. Mech. 1955. – № 22. – Р. 215–221.

3. http://e-science.ru/math/theory/?t=318

2. Динамика манипуляторов

2.1. Уравнения Лагранжа II рода

Из курса механики известны уравнения Лагранжа II рода, которые связывают обобщенные силы Q₁(t), Q₂(t), ..., Q_n(t), прилагаемые к системе материальных точек, с обобщенными кординатами q₁(t), q₂(t), ..., q_n(t), описывающими движение системы материальных точек под воздействием вышеуказанных сил. Уравнения Лагранжа II рода имеют вид

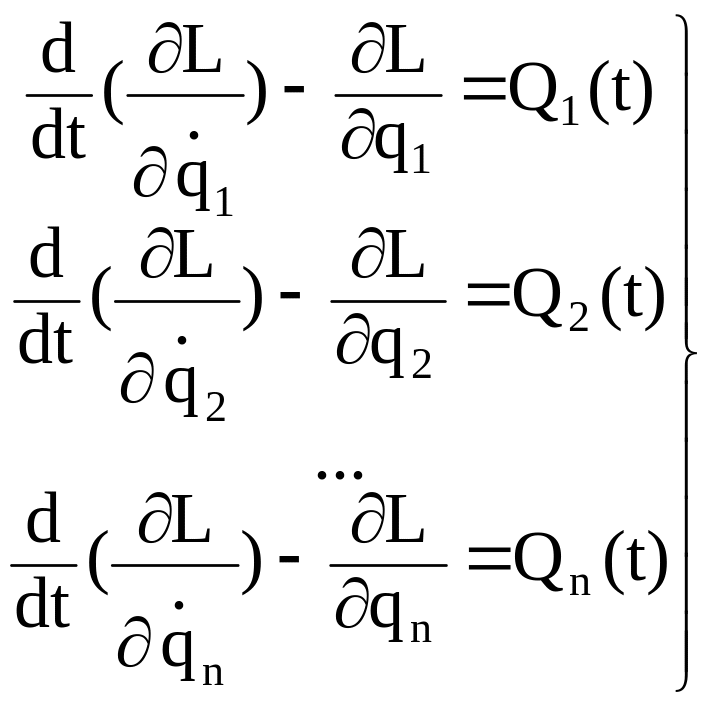, (2.1)

где L = К – П – функция Лагранжа; К – кинетическая энергия системы материальных точек; П – потенциальная энергия системы материальных точек; q₁ (t), q₂ (t), ..., q_n (t) – обобщенные координаты, описывающие движение системы; Q₁ (t), Q₂ (t), ..., Q_n (t) – обобщенные силы, прилагаемые к системе; n – число степеней свободы системы. Если q_k – угол вращения, то Q_k следует понимать как момент силы, а если q_k является линейным перемещением, то Q_k – приложенная сила. Уравнения Лагранжа справедливы для голономных систем материальных точек, в число которых входят и рассматриваемые нами манипуляторы.

Вычислим К и П, подставим их в формулу (2.1) и получим систему уравнений, описывающих динамику манипулятора. При дальнейшем изложении эту систему мы будем для краткости называть уравнением динамики манипулятора.

2.2. Кинетическая энергия манипулятора

Кинетическая энергия манипулятора равна сумме кинетических энергий его звеньев:

K = . (2.2)

Кинетическая энергия i-го звена равна сумме кинетических энергий составляющих это звено точек:

K_i = dK₁ + dK₂ + ... (2.3)