Библиографический список

1. Егоров А.С., Планирование путей в среде с известными запрещенными состояниями. Отчет по гранту РФФИ №05-08-01199а. Красноярск. СибГАУ, 2008.

2. Черников, С. Н. Линейные неравенства. – М: Наука, 1968.

3. H. Choset et al., “Principles of Robot Motion. Theory, Algorithms and Implementations”, A Bradford Book. The MIT Press. 2005.

.

3.6.7. Алгоритм разделения ячеек

При планировании пути целесообразно конфигурационное пространство разделять на области (ячейки), состоящие либо только из разрешенных точек либо только из запрещенных точек. Впоследствии при планировании пути можно будет оперировать не отдельными точками, как это делалось в предыдущих параграфах, а их совокупностями, что в перспективе может привести к более быстрому планированию пути.

Рассмотрим алгоритм разделения конфигурационного пространства на области (ячейки) свободных и запрещенных точек и планирования пути [Корицкий].

В пространстве обобщённых координат препятствия представлены точками, которые соответствуют запрещённым конфигурациям манипулятора, т.е. тем конфигурациям, в которых робот какой-нибудь своей точкой пересекается с препятствием. Соответственно, мы не можем проводить границы ячеек от углов препятствий, представленных в таком виде. Поэтому рассмотрим, что представляет собой ячейка в пространстве обобщённых координат, а так же введём новые понятия – свободная область и пустое пространство.

Разделение пространства обобщённых координат на ячейки будем проводить через шаг дискретизации, принятый в «Точном алгоритме». Ячейкой считается множество точек, находящихся на одной линии дискретизации, т.е. один элемент вектора координат каждой точки имеет одинаковое значение. Например, для манипулятора с двумя подвижными звеньями, координата первого звена которого d₁ (абсцисса), а второго – d₂ (ордината), ячейку можно представить как на рисунке 1. Координаты d₁ и d₂ обозначают номера вертикальной и горизонтальной линий сетки дискретизации соответственно.

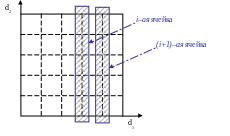
Рисунок 1 – Ячейки в пространстве обобщённых координат

Здесь векторы координат каждой точки рабочего пространства (d₁, d₂), принадлежащие одной ячейке, имеют одинаковый элемент – d₁.

Ячейки необходимо пронумеровать, но так как они располагаются на каждом шаге дискретизации, то номер ячейки будет совпадать с координатой узла сетки дискретизации, одинаковой для каждой точки данной ячейки, т.е. с d₁.

Для манипулятора с тремя подвижными звеньями к существующим координатам первого звена d₁ и второго – d₂, добавляется третье звено d₃ (аппликата). Таким образом пространство обобщенных координат для трехзвенного манипулятора трехмерно и может быть представлено, как множество плоскостей двумерного пространства обобщенных координат. (См. рис. 2)

(i+1)-ая плоскость

i -ая плоскость

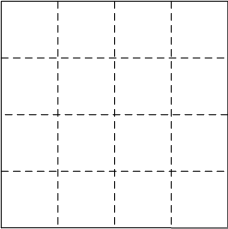
Рисунок 2 – Пространство обобщенных координат для трехмерного разделения ячеек

Алгоритм разделения ячеек для трехмерного случая подобен алгоритму разделения ячеек для двумерного случая. Основная особенность алгоритма для трехмерного случая в том, что рассматривается не одна плоскость включающее двумерное пространство, а их множество подобно слоям один за другим. В каждой плоскости ищется пространство свободное от запрещенных точек. Для этого применяется способ двумерного разделения ячеек. И если на какой-нибудь плоскости в некоторой ячейке есть запрещённые конфигурации, т.е. ячейка содержит множества запрещённых точек и множества разрешённых точек, причём запрещённые точки располагаются между разрешёнными (или наоборот, что не меняет смысл), то можно говорить о свободных областях ячейки. Свободная область ячейки – это множество разрешённых точек ячейки, между которыми нет ни одной запрещённой точки.

Каждая свободная область характеризуется (2n-1) параметрами, где n – количество подвижных звеньев манипулятора. Например, для манипулятора с двумя подвижными звеньями свободная область характеризуется тремя параметрами, где первый параметр – номер ячейки, второй – крайняя нижняя точка свободной области и третий – крайняя верхняя точка свободной области.

Возможны случаи, когда ячейка не содержит ни одной запрещённой точки, т.е. вся ячейка является одной своей свободной областью, такую ячейку назовём свободной. А множество идущих подряд свободных ячеек образуют – пустую область пространства обобщённых координат или просто пустое пространство.

Введём следующие обозначения (для трехзвенного манипулятора):

K – количество плоскостей;

I – количество ячеек;

J – количество точек, полученных при дискретизации по вертикали;

A – количество свободных областей в ячейке, 1 ≤ А ≤ J/2.

B – количество точек в одной свободной области, 1 ≤ В ≤ J.

Пространство свободное от запрещенных точек или пустое пространство объединяется в каждой плоскости и между плоскостями. При этом происходит соединение в последовательности тех свободных областей, в которых возможен беспрепятственный переход из одной плоскости в другую. Затем проверяется достижимость конечной точки q^T и если достижимость подтверждается, то происходит построение маршрута на основе последовательности свободных областей. Пробное предварительное построение производится на начальных этапах алгоритма, для того чтобы найти наилучший путь в простых случаях и исключить затраты времени и ресурсов для составление алгоритма разделения ячеек для подобных случаев.

Основные этапы алгоритма трехмерного разделения ячеек:

1. Предварительный поиск маршрута;

2. Разделение каждой плоскости на свободные области, построение TFR;

3. Соединение в последовательности тех свободных областей, в которых возможен беспрепятственный переход из одной в другую для каждой плоскости, построение LCR;

4. Объединение свободных соединенных областей в единое свободное пространство для каждой плоскости в случае если области не отделены от друг друга, построение ETFR;

5. Соединение свободных областей на соседних плоскостях или межплоскостное объединение свободных областей, построение ELCR;

6. Проверяется достижимость точек q⁰ и q^T через сравнение единых областей в которых находятся эти точки, построение TUR;

7. Построение маршрута на основе достижимой комбинации областей.

Более подробно об этапах алгоритма и особенностях построения траектории рассказано в следующих пунктах.