Вспомогательная таблица для расчета параметров уравнений линейного и квадратического тренда

Период реаль-ного времени	Условное обозначение времени			yxt	y xt2	y xt4
	Условное t	Условное t2	Условное t4
2001	–2	4	16
2002	–1	1	1
2003	0	0	0
2004	1	1	1
2005	2	4	16
Сумма:	0	10	34

Формулы для расчета параметров тренда будут иметь следующий вид:

а) для линейного тренда (y = a₀ + a₁t):

(10.7)

б) для уравнения квадратического тренда, т.е. параболы

(y = a₀ + a₁t + a₂t²):

(10.8)

Необходимо обратить внимание, что параметр a₁ рассчитывается по такой же формуле, как и для линейного тренда.

Обычно при построении уравнений тренда или регрессии возникает проблема выбора такой математической формы зависимости, которое лучше сглаживает исходный ряд данных.

Для этого используют различные способы, в том числе графический анлиз, или, как уже отмечалось, рассчитывается ошибка аппроксимации и выбирается то из уравнений, для которого эта ошибка меньше. Помимо ошибки аппроксимации, существуют и другие критерии оценки надежности построенных уравнений и отбора тех, которые наиболее адекватно описывают реальную статистическую зависимость. Более подробно эти критерии изучают в курсе эконометрики. В частности, можно рассчитать корреляционное отношение или индекс детерминации (квадрат корреляционного отношения) и оценивать, насколько эти показатели близки к 1.

4. Расчет корреляционного отношения на основе уравнения регрессии

Корреляционное отношение является одним из показателей тесноты связи, которая рассчитывается для оценки степени тесноты связи, если зависимость между двумя показателями не является линейной (т.е. линейный коэффициент корреляции может не показать наличие связи).

Для расчета корреляционного отношения необходимо вначале построить уравнение парной регрессии, выражающее зависимость между показателями x и y .

Пусть y = f(х) – уравнение парной регрессии.

Если уже рассчитаны его параметры, необходимо рассчитать все теоретические (или расчетные) значения показателя y – так же, как это делается при расчете ошибки аппроксимации.

Затем корреляционное отношение рассчитывается по фор­муле:

где – дисперсия теоретических значений y;

– дисперсия фактических значений y.

В этой формуле где f(х) – построенное уравнение регрессии.

Для расчета корреляционного отношения η строится обычно вспомогательная таблица следующего вида (табл.10.3):

Таблица 10.3

Вспомогательная таблица для расчета корреляционного отношения

	y	yх	yх – ух	( yх – yх)2
х1	y1	f(х)
х2	y2	f(x)
х3	y3	f(x)
.	.
хn	yn	f(x)
	Σ	Σ	Σ	Σ

Корреляционное отношение обладает свойством: 0 ≤ η ≤ 1.

Чем ближе η к 1, тем связь более тесная. Для оценки степени тесноты связи с помощью корреляционного отношения используется специальная шкала, которую называют шкалой Чеддока (по имени автора, предложившего данную шкалу).

Шкала Чеддока

Значение η	0,1–0,3	0,3–0,5	0,5–0,7	0,7–0,9	0,9–0,999
Теснота связи	Слабая	Умеренная	Заметная	Высокая	Очень высокая

Рекомендуется рассчитывать корреляционное отношение в тех случаях, если линейный коэффициент корреляции не показывает наличия тесной связи между признаками, однако есть основание считать, что связь все же имеется, но не является линейной.

В теории статистики различают понятия «теоретическое корреляционное отношение» и «эмпирическое корреляционное отношение». Приведенная выше формула соответствует понятию «эмпирическое корреляционное отношение».

Теоретическое корреляционное отношение может быть рассчитано до построения уравнения регрессии на основе результатов аналитической группировки данных.

Для расчета теоретического корреляционного отношения используются сгруппированные (по факторному признаку) данные, для которых находится межгрупповая и общая дисперсия результативного признака y. Затем находится отношение этих дисперсий и извлекают из них корень, то есть рассчитывают η по формуле:

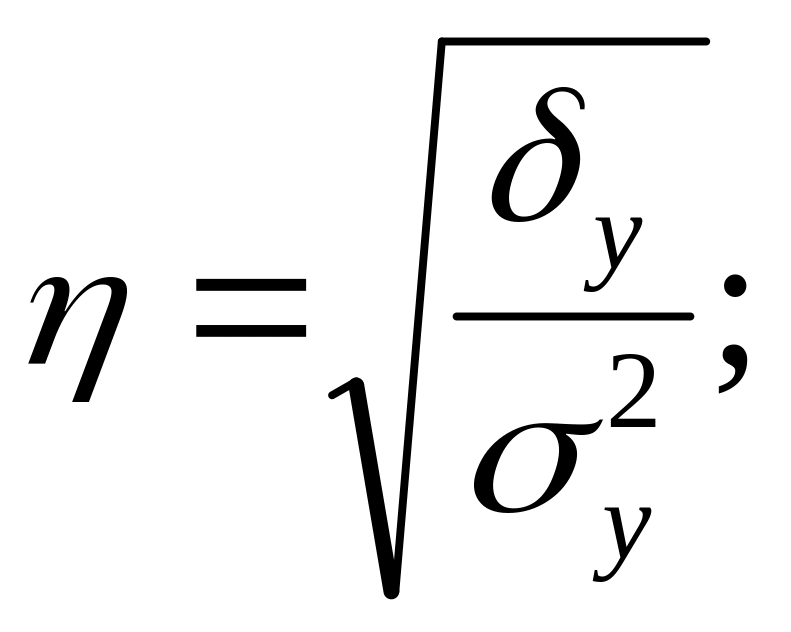
^{- межгрупповая дисперсия признака y}

- общая дисперсия признака y

Теоретическое корреляционное отношение, в отличие от эмпирического, может быть определено до построения уравнения регрессии, но оно более приближенно характеризует связь между признаками x и y. И для того, и другого показателя выполняется условие 0 ≤ η ≤ 1 (межгрупповая дисперсия всегда меньше общей дисперсии).

Оба показателя характеризуют долю вариации результативного признака, объясняемой за счет вариации факторного (группировочного) признака x.

В заключение отметим, что квадрат корреляционного отношения, т.е. показатель R² = , в числителе которого стоит дисперсия расчетных значений результативного признака, а в знаменателе – дисперсия изначальных (эмпирических) данных, называется в статистике индексом детерминации.

Для этого показателя также выполняется соотношение 0 < R² < 1, и он характеризует не только тесноту связи между факторным и результативным признаком, но и то, насколько адекватно построенное уравнение описывает реальную статистическую зависимость между переменными. Индекс детерминации, наряду с ошибкой аппроксимации, используется для оценки значимости (надежности) построенных уравнений и отбора наилучшей формы математической зависимости.

Преимущество индекса детерминации и корреляционного отношения перед другими показателями тесноты связи в том, что они могут оценивать не только линейные, но и нелинейные зависимости, а также использоваться для оценки уравнений множественной регрессии.

Лекция №11. Построение уравнений парной нелинейной и множественной регрессии

Введение.

При построении уравнений парной нелинейной регрессии и уравнений множественной регрессии нередко возникают дополнительные трудности. Эти трудности связаны с тем, что, во-первых, метод наименьших квадратов (МНК) изначально разработан для расчета параметров линейных функций и в его основу заложены некоторые предпосылки, которые всегда выполняются для линейных уравнений регрессии, но могут быть нарушены, если МНК применяется для расчета параметров линеаризованных (но изначально не линейных) уравнений регрессии.

Во-вторых, при построении уравнений множественной регрессии одной из важнейших проблем становится проблема отбора тех факторов, которые целесообразно включать в уравнение. В 30-е г. XX в. увлечение множественной регрессией сменилось разочарованием. Стремясь включить как можно больше факторов в модель, исследователи часто сталкивались с бессмысленными результатами. В настоящее время считается, что в уравнение множественной регрессии не имеет смысла включать более трех-четырех факторных признаков.