
Беляев Ю.Н. Введение в векторный анализ
.pdfФедеральное агентство по образованию
ГОУ ВПО ½Сыктывкарский государственный университет\
Ю.Н. БЕЛЯЕВ
ВВЕДЕНИЕ В ВЕКТОРНЫЙ
АНАЛИЗ
Учебное пособие
Сыктывкар 2008
2
ÓÄÊ 514.742.4(075) ÁÁÊ 22.14
Á 43
Печатается по постановлению редакционно-издательско- го совета Сыктывкарского госуниверситета
Ðå ö å í ç å í ò û:
кафедра математического анализа Коми государственного педагогического института,
Г.В. Уфимцев канд. физ.-матем. наук, доцент, Сыктывкарский лесной институт
Беляев Ю.Н.
Á 43 Введение в векторный анализ: Учебное пособие. Сыктывкар: Из-во СыктГУ, 2008. 215 с.: ил.
ISBN 978-5-87237-601-1
Данное пособие содержит основные сведения из алгебры векторов.
Правила дифференцирования вектор-функции по скалярному аргументу демонстрируются на примерах из механики, в частности из кинематики материальной точки и абсолютно тв¼рдого тела.
Основные функции точки градиент скалярного поля, расхождение и вихрь векторного поля даны в инвариантной по отношению к выбору системы координат форме. Интегральное представление вихря и расхождения векторного поля используются для доказательства теорем Остроградского и Стокса. Даны подборка формул для градиента, дивергенции, ротора и оператора Лапласа в некоторых ортогональных системах координат, а также задачи для самостоятельной работы студентов с примерами решения типовых задач, используемых для контроля усвоения материала.
Книга предназначена для студентов физических специальностей.
c Беляев Ю.Н., 2008
c Сыктывкарский госуниверситет, 2008
ISBN 978-5-87237-601-1
Оглавление
à ë à â à 1. |
Основные сведения из алгебры векторов |
7 |
Ÿ 1. Геометрическое понятие вектора . . . . . . . . . . . . . . |
7 |
|
1.1. |
Введение. . . . . . . . . . . . . . . . . . . . . . . . . |
7 |
1.2. Скаляры и векторы. . . . . . . . . . . . . . . . . . . |
7 |
|
1.3. |
Изображение и обозначения векторных величин. . |
8 |
1.4. |
Равенство векторов. . . . . . . . . . . . . . . . . . . |
9 |
1.5.Умножение вектора на число. . . . . . . . . . . . . 10
1.6.Сложение векторов. . . . . . . . . . . . . . . . . . . 11
1.7.Основные свойства векторов. . . . . . . . . . . . . . 11
1.8.Правило многоугольника. . . . . . . . . . . . . . . . 13
1.9.Разность векторов . . . . . . . . . . . . . . . . . . . 14
Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
Ÿ2. Примеры векторов . . . . . . . . . . . . . . . . . . . . . . 17
2.1.Радиус-вектор точки. . . . . . . . . . . . . . . . . . 17
2.2.Перемещение, скорость и ускорение . . . . . . . . . 22
2.3.Понятие силы. . . . . . . . . . . . . . . . . . . . . . 25
Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
Ÿ3. Линейное пространство . . . . . . . . . . . . . . . . . . . 28
3.1.Примеры линейных пространств. . . . . . . . . . . 29
3.2.Размерность и базис линейного пространства. . . . 34
Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
36 |
Ÿ 4. Разложение вектора на составляющие . . . . . . . . . . |
37 |
4.1.Векторный базис. . . . . . . . . . . . . . . . . . . . 38
4.2.Свойства координат вектора. . . . . . . . . . . . . . 39
4.3.Размерность векторного множества. . . . . . . . . . 40
Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
Ÿ5. Проекции вектора . . . . . . . . . . . . . . . . . . . . . . 43
5.1.Проекция вектора на плоскость. . . . . . . . . . . . 43
5.2.Проекция вектора на ось. . . . . . . . . . . . . . . . 44
5.3.Свойства проекции вектора на ось. . . . . . . . . . 45
3
4
Ÿ6. Приложение к тригонометрии . . . . . . . . . . . . . . . 46
6.1.Проекции единичного вектора. . . . . . . . . . . . . 46
6.2.Тригонометрическая форма записи проекции. . . . 46
6.3.Основное тригонометрическое тождество . . . . . . 47
6.4.Формулы приведения. . . . . . . . . . . . . . . . . . 47
6.5.Теорема синусов. . . . . . . . . . . . . . . . . . . . . 47
Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
50 |
Ÿ 7. Вектор в ортонормированном базисе . . . . . . . . . . . |
50 |
7.1.Координаты вектора в ортонормированном базисе. 50
7.2.Длина вектора . . . . . . . . . . . . . . . . . . . . . 52
7.3.Направляющие косинусы. . . . . . . . . . . . . . . . 52
7.4.Угол между направлениями. . . . . . . . . . . . . . 52
7.5.Радиус-вектор в декартовой системе координат . . 53
7.6.Определение векторной суммы методом проекций. 55
Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
Ÿ8. Скалярное произведение векторов . . . . . . . . . . . . . 59
8.1.Cвойства скалярного произведения. . . . . . . . . . 60
8.2.Евклидовое пространство. . . . . . . . . . . . . . . 61
8.3.Теорема косинусов. . . . . . . . . . . . . . . . . . . 61
8.4.Скалярное произведение в ортонормированном базисе. . . . . . . . . . . . . . . . . . . . . . . . 63
Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
Ÿ9. Векторное произведение векторов . . . . . . . . . . . . . 68
9.1.Свойства векторного произведения. . . . . . . . . . 69
9.2.Векторное произведение в ортонормированном базисе. . . . . . . . . . . . . . . . . . . . . . . . 70
9.3.Выражение векторного произведения через
|
оределители второго и третьего порядков. . . . . . |
71 |
|
Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
73 |
Ÿ 10. Произведения тр¼х векторов . . . . . . . . . . . . . . . . |
76 |
|
|
10.1. Смешанное произведение . . . . . . . . . . . . . . . |
76 |
|
10.2. Двойное векторное произведение . . . . . . . . . . |
78 |
à ë à â à |
2. Вектор-функция скалярного аргумента |
79 |
Ÿ 1. |
Производная вектор-функции по скалярному аргументу |
79 |
1.1.Геометрический смысл производной. . . . . . . . . 79
1.2.Основные свойства производных. . . . . . . . . . . 82
Ÿ2. Интеграл от вектора . . . . . . . . . . . . . . . . . . . . . 89
Ÿ3. Оси естественного тр¼хгранника . . . . . . . . . . . . . . 91
3.1.Формулы Френе. . . . . . . . . . . . . . . . . . . . . 93
3.2.Скорость и ускорение в осях натурального триэдра. 96
3.3.Вычисление кривизны пространственной кривой. . 99
5
3.4.Кручение пространственной кривой. . . . . . . . . 103 Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104
Ÿ4. Криволинейные ортогональные системы координат . . . 104
4.1.Базисные векторы и коэффициенты Ламе. . . . . . 107
4.2.Скорость и ускорение материальной точки в криволинейной ортогональной системе координат. 108
Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111
Ÿ5. Сложение движений. Приложение к кинематике. . . . . 112
5.1.Перемещение системы отсч¼та. Угловая скорость. 113
5.2.Скорости точек тв¼рдого тела. . . . . . . . . . . . . 116
5.3.Ускорения тв¼рдого тела. . . . . . . . . . . . . . . . 118
5.4.Абсолютная скорость движения материальной точки. . . . . . . . . . . . . . . . . . . . . . . . . 120
5.5.Сложение ускорений. . . . . . . . . . . . . . . . . . 125 Задачи. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131
à ë à â à 3. Функции точки |
133 |
Ÿ1. Скалярное поле . . . . . . . . . . . . . . . . . . . . . . . . 133
1.1.Поверхность уровня скалярного поля. . . . . . . . 133
1.2.Дифференцируемое скалярное поле. . . . . . . . . 134
1.3.Производная по направлению. . . . . . . . . . . . . 135
1.4.Геометрический смысл градиента. . . . . . . . . . . 136
1.5.Градиент суммы. . . . . . . . . . . . . . . . . . . . . 137
1.6.Градиент сложной функции. . . . . . . . . . . . . . 141
1.7.Градиент в ортогональной системе координат. . . . 143 Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 146
Ÿ2. Векторное поле . . . . . . . . . . . . . . . . . . . . . . . . 148
2.1.Уравнение векторной линии. . . . . . . . . . . . . . 148
2.2.Криволинейный интеграл от векторного поля. . . . 151
2.3.Вычисление криволинейного интеграла . . . . . . . 153
2.4.Вихрь векторного поля. . . . . . . . . . . . . . . . . 156
2.5. |
~ |
160 |
Смысл вектора rot P . . . . . . . . . . . . . . . . . . |
||
2.6. |
Потенциальное векторное поле. Скалярный |
|
|
потенциал. . . . . . . . . . . . . . . . . . . . . . . . |
161 |
Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
163 |
|
Ÿ 3. Поток векторного поля . . . . . . . . . . . . . . . . . . . |
163 |
|
3.1.Поток скорости . . . . . . . . . . . . . . . . . . . . . 164
3.2.Поток векторного поля. . . . . . . . . . . . . . . . . 166
3.3.Нормаль к поверхности. . . . . . . . . . . . . . . . . 167
3.4.Вычисление потока. . . . . . . . . . . . . . . . . . . 168
3.5.Поток через замкнутую поверхность. . . . . . . . . 170 Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 170
6
Ÿ 4. Расхождение векторного поля . . . . . . . . . . . . . . . 171
4.1.Расхождение в ортогональной системе координат . 172
4.2.Соленоидальное векторное поле. Векторный потенциал. . . . . . . . . . . . . . . . . . . . . . . . 175
4.3.Лапласово векторное поле. . . . . . . . . . . . . . . 175 Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 176
Ÿ5. Символические обозначения основных дифферен-
циальных операций . . . . . . . . . . . . . . . . . . . . . 177
5.1.Символический вектор набла . . . . . . . . . . . . . 177
5.2.Оператор Лапласа, . . . . . . . . . . . . . . . . . . . 178
5.3.Производная вектора по другому вектору . . . . . 179
5.4.Дифференциальные операции от произведений функций. . . . . . . . . . . . . . . . . . . . . . . 179
5.5.Дифференциальные операции второго порядка . . 183 Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 184
Ÿ6. Некоторые ортогональные системы координат . . . . . . 184
6.1.Система цилиндрических координат. . . . . . . . . 185
6.2.Сферическая система координат. . . . . . . . . . . 186
6.3.Система параболических цилиндрических координат. . . . . . . . . . . . . . . . . . . . . . . . . 187
6.4.Система параболоидальных координат. . . . . . . . 188
6.5.Система эллиптических цилиндрических координат. 189
6.6.Система вытянутых эллипсоидальных координат. 190 Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 191
Ÿ7. Теорема Стокса . . . . . . . . . . . . . . . . . . . . . . . . 192 Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 195
Ÿ 8. Теорема Остроградского и связанные с ней формулы . 195
8.1.Теорема Остроградского. . . . . . . . . . . . . . . . 195
8.2.Формула для градиента. . . . . . . . . . . . . . . . 201
8.3.Формула для вихря. . . . . . . . . . . . . . . . . . . 201
8.4.Формулы Грина. . . . . . . . . . . . . . . . . . . . . 202 Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206
Библиографический список . . . . . . . . . . . . . . . . . . . 207 Ответы и решения . . . . . . . . . . . . . . . . . . . . . . . . 209
Глава 1
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ ВЕКТОРОВ
Ÿ1. Геометрическое понятие вектора
1.1.Введение. Одно из основных геометрических понятий вектор, возникло как математическая абстракция объектов, характеризующихся величиной и направлением, в трудах нескольких ученых почти одновременно в середине XIX века. Первое векторное исчисление на плоскости развил в 1835 году итальянский ученый Беллавитис (Guito Bellavitis, 1835-1880). Примерно в это же время получили известность работы Аргана (Jean Robert Argand, 1768-1822) и Весселя (Caspar Wessel, 17451818) о геометрической интерпретации комплексных чисел. Окончательное оформление векторной алгебры было выполнено в работах Германа Грассмана (Hermann Grassmann, 18091877), Уильяма Гамильтона (William Rowen Hamilton, 18051865) и Дж.У. Гиббса (Josiah Willard Gibbs, 1839-1903).
Понятие вектора играет важнейшую роль в современной математике и е¼ приложениях, например в механике, теории относительности, электродинамике, квантовой физике и других разделах естествознания.
1.2.Скаляры и векторы. Величины называются скалярными (скалярами), если они после выбора единицы измерения полностью характеризуются одним числом. Примерами скаляров являются время t, объем V , масса m, температура T , работа силы A, электрический заряд q и др.
Два скаляра одной и той же размерности равны, если при измерении их одной и той же единицей меры получаются оди-
наковые числа.
!
Такие величины, как скорость ~v, ускорение ~a, сила F , на-
!
пряженность электрического поля E , требующие для своего за-
7
8 |
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
дания не только указания числового значения, но и направления в пространстве, называются векторными величинами, или
векторами.
Термины скаляр (1843) и вектор (1845) были придуманы Гамильтоном, который образовал их соответственно от латинских слов scale шкала и vector несущий.
Простейшим скаляром является отвлеченное число, а простейшим вектором прямолинейный отрезок, имеющий определенную длину и определенное направление от начальной точ- ки отрезка к его конечной точке.
1.3. Изображение и обозначения векторных вели- чин. Существует несколько различных форм обозначения векторных величин. Одна из старейших черточка над буквой. Именно так обозначал направленный отрезок Арган. Максвелл (James Clerk Maxwell, 1831-1879) обозначал векторы готическими буквами, Гамильтон и Гиббс греческими буквами. Обозначение векторов жирными буквами было предложено Хэвисайдом (Oliver Heaviside, 1850-1925).
В данной работе геометрические векторы обозначаются бук-
~
вами со стрелкой вверху: ~a, b, ~c и т.п. Иногда мы будем обо-
значать вектор, начальная точка которого есть A, а конечная
!
B, символом AB. На рисунках векторы изображаются в виде прямолинейных отрезков, имеющих не только определенную длину, но и определенное направление, указываемое стрелкой на конце отрезка.
Длина вектора, которая иначе называется модулем вектора, обозначается той же буквой, что и вектор, но без стрелки. Иногда для обозначения модуля вектора берется обозначение самого вектора, помещенного в прямые скобки. Например, p = jp~j модуль вектора p~.
~
Нуль-вектор вектор 0, длина которого равна нулю, может иметь любое направление в пространстве.
Угол между векторами p~ и q~ это наименьший угол, на который нужно повернуть один вектор, чтобы он совпал по направлению с другим (рис.1). Будем обозначать этот угол сим-
d
волом (p;~ q~).

Ÿ 1. Геометрическое понятие вектора |
9 |
1.4. Равенство векторов. Когда мы сравниваем векторные физические величины, то подразумевается, что они имеют одинаковую физическую размерность.
Различают три разных типа векторов. Каждый из них объединяет совокупность векторов с одинаковыми свойствами.
Свободные векторы определяются направлением линии действия и модулем. Такие векторы равны, если они равны по мо-
d
~
дулю f = g и одинаково направлены, т.е. (f; ~g) = 0: Иными
~
словами, мы не различаем двух свободных векторов f и ~g, имеющих разные точки приложения и получающиеся один из другого параллельным переносом.
~
Равенство двух векторов f и ~g символически записывается следующим образом:
~
f = ~g:
!Связанный вектор. Для определения связанного вектора AB требуется указать его линию действия (на рис. 2a это линия xx0), направление на этой линии (от x к x0), его начало (A) и длину вектора. Связанные векторы это векторы, для эквивалентности которых необходимо их равенство по длине, одинаковое направление и общее начало. Примером такого вектора может служить сила, приложенная к некоторой точке упругого
òåëà. |
|
|
x0 |
x0 |
|
|
|
|
|||
|
|
|
|
|
B0 |
q~ |
|
|
|
A0 |
|
|
|
a) |
b) |
|
|
c |
|
B |
|
||
|
A |
A |
|
||
) (p;~ q~) |
p~ |
B |
|
|
|
|
|
|
|
|
|
Ðèñ. 1 |
Ðèñ. 2 |
|
|
|
|
|
|
x |
x |
|
|
Скользящий вектор. Определение остается таким же, как и в предыдущем случае, если исключить требование о закреплении начала вектора. Оно может находиться в любой точке оси xx0. Скользящими называют такие векторы, которые счита-
ются эквивалентными, если они равны по модулю, одинаково
! !0 0
направлены и лежат на одной прямой (например, AB = A B на (рис. 2b)). Примерами таких векторов являются силы, рас-
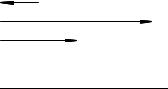
10 |
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
сматриваемые в статической механике.
Поскольку направлние нулевого вектора не определено, все нулевые векторы считаются равными.
Все нижеследующие правила, в частности умножение вектора на скалярные величины и правило сложения векторов, будут даны применительно к свободным векторам. Распространение этих определений на связанные и скользящие векторы не представляет труда.
1.5. Умножение вектора на число. При умножении вектора ~a на действительное число получается вектор ~c, такой, что его модуль равен j ja, и направленный в ту же сторону, что и вектор ~a при > 0, и в противоположную сторону, если < 0. Умножение любого вектора ~a на нуль дает нулевой вектор. Таким образом,
|
> |
|
|
d |
|
|
< |
~c; c = a; (~c;~a) = 0; åñëè > 0; |
|
||
|
~ |
|
|
|
|
~a = ~a = |
> |
0; åñëè = 0:d |
(1.1) |
||
8 |
~c; c = |
|
a; (~c;~a) = ; åñëè < 0; |
||
|
: |
|
|
|
|
Векторы ~c и ~a, связанные равенством (1.1), параллельны друг другу или лежат на одной прямой. Такие векторы называют коллинеарными 1.
На рис. 3 в качестве примера показаны вектор ~a и полу- чающиеся из него в результате умножения на числа 2 и 0:5 векторы 2~a и 0:5~a.
0:5~a
2~a
~a
Ðèñ. 3
В соответствии с данным определением умножения вектора на число любой вектор ~a можно представить в виде произведения
~a = a~ea; |
(1.2) |
1Термин образован от латинских co вместе è linearis линейный и означает буквально ½солинейность\. Гамильтон в своем векторном исчис-
лении ввел название termino-collinear для векторов, которые имеют общее начало и концы которых лежат на одной прямой. Это название упростил Гиббс, благодаря которому термин ½коллинеарность\ вошел в векторную
алгебру (1901).
