Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4614 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Сыктывкарский Государственный Университет им. Питирима Сорокина
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Беляев Ю.Н. Введение в векторный анализ

.pdf
Скачиваний:
401
Добавлен:
29.03.2016
Размер:
1.13 Mб
Скачать
☆

Ÿ 6. Некоторые ортогональные системы координат

191

Для однозначного задания всех точек пространства измене-

ния координат , ', ограничим следующими интервалами

 

 

 

 

 

0 < +1; 0 ' ; 0 < 2 :

 

 

 

 

 

Координаты , ', связаны с декартовыми координатами

x, y и z соотношениями

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x = a sh sin ' sin ;

 

 

 

 

 

 

y = a sh sin ' cos

 

 

 

 

;

 

 

 

 

z = a ch cos ':

 

Коэффициенты Ламе:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

H = H' = aq

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ch2 cos2 ';

 

H

 

 

 

 

= a sh sin ';

 

 

 

 

 

квадрат элемента длины равен

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ds2 = a2(ch2 cos2 ')(d 2 + d'2) + a2 sh2 sin2' d

2:

 

 

 

Положим q

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

= , тогда

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ch2 cos2 '

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

grad U =

 

1 @U

 

~e +

1 @U

~e' +

 

 

 

 

1

 

 

 

 

 

 

 

@U

 

~e

 

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a @

 

a

@'

 

a sh sin '

@

 

 

 

 

 

 

 

 

 

 

 

 

 

 

div P~ =

1

 

 

 

 

2 sh2 + sin2 '

 

P +

2 sin2

' + sh2

P' +

 

 

 

 

 

 

a 3

 

 

 

 

 

 

 

th

 

 

 

 

 

 

 

 

 

 

 

 

 

 

tg '

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

@P

 

 

 

 

 

 

@P'

 

 

 

 

 

1

 

 

 

 

 

 

 

 

@P

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

+

 

 

 

 

 

 

 

 

 

 

 

+

 

 

 

 

 

 

 

+

 

 

 

 

 

 

 

 

 

 

 

 

 

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

 

 

@

 

 

@'

a sh sin '

@

 

 

 

 

 

 

rot P~ =

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

@P

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

@P

'

~e +

 

 

 

 

 

 

 

 

 

 

 

P

+

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a tg '

 

 

 

@'

 

 

a sh sin '

@

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

@P

 

 

 

1

 

 

 

 

 

1

 

 

 

 

 

 

 

 

@P

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

+

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P +

 

 

 

 

 

 

 

~e' +

 

 

 

 

 

 

a sh sin '

@

 

 

 

a

 

 

th

 

@

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

@P

 

 

@P

 

 

 

 

 

 

+

 

 

 

(sh ch P' sin ' cos 'P )+

 

 

 

 

'

 

 

~e ;

 

 

a 3

a

 

@

@'

 

r2U =

1

 

 

 

 

 

 

1 @U 1 @U

 

 

 

 

@2U

 

 

 

@2U

 

 

 

 

 

 

 

 

 

 

1

 

 

 

@2U

 

 

 

 

 

 

 

 

+

 

 

 

 

 

+

 

 

+

 

 

 

+

 

 

 

 

:

 

a2 2

th

@

 

 

tg '

@'

 

 

@ 2

@'2

 

 

a2 sh2 sin2'

@ 2

Задачи 103. Используя формулы (3.18), (3.62), (3.40) и (3.84), полу-

чить выражения для градиента скалярного поля, расхождения и вихря векторного поля, оператора Лапласа в:

192

Глава 3. ФУНКЦИИ ТОЧКИ

1)цилиндрической системе координат (см. стр. 185);

2)сферической системе координат (см. стр. 186);

3)системе параболических цилиндрических координат (см. стр. 187);

4)системе параболоидальных координат (см. стр. 188);

5)системе эллиптических цилиндрических координат (см. стр. 190).

6)системе вытянутых эллипсоидальных координат (см. стр.

191).

104. Вычислить градиент скалярного поля U (M ), заданного в цилиндрической и сферической системах координат: 1)

U ( ; '; z) = a + b ' + cz, 2) U ( ; '; z) = 'z, 3) U (r; ; ') = r ', 4) U (r; ; ') = ar2 + br2( + ')2 , где a, b, c некоторые постоянные.

105. Вычислить дивергенцию и ротор векторного поля

~

P (M ), заданного в цилиндрической и сферической системах координат:

1)

~

 

 

 

P ( ; '; z) = ~e cos ' ~e' + z~ez ;

 

2)

~

 

2

~ez ;

P ( ; '; z) = cos ' ~e (1= )~e'

3)

~

2

~er + cos ~e '~e';

 

P (r; ; ') = r

 

4)

~

 

 

 

P (r; ; ') = cos ~er + sin ~e + r~e':

Ÿ 7. Теорема Стокса

Рассмотрим замкнутый контур L, стягивающий двустороннюю поверхность . Положительное направление нормали ~en к поверхности связано с положительным направлением обхода е¼ границы контура L. А именно: положительный обход контура L выбирается таким образом, чтобы поверхность оставалась слева для наблюдателя, так что вектор положительной нормали в точках у контура направлен от ног к голове наблюдателя.

Пусть во всех точках этой поверхности заданы и непрерыв-

~

ны компоненты вектора P и их частные производные по координатам.

Ÿ 7. Теорема Стокса

193

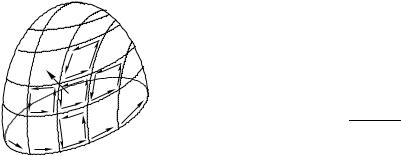
Разобъ¼м поверхность на N достаточно малых частей i, ограниченных замнутыми контурами `i. На каждом из элементарных участков поверхности i возьм¼м единичный вектор нормали ~eni и установим направление обхода контуров `i

согласно правилу правого винта (см. рис. 94).

 

 

 

 

 

 

 

Согласно

определнию

(3.31),

 

 

 

проекция вихря векторного по-

 

 

ëÿ

~

в некоторой точке Mi, ïðè-

 

 

 

P

~eni

 

 

надлежащей площадке i, íà íà-

 

 

правление нормали ~eni

 

 

 

 

 

 

 

i

 

 

 

 

 

 

 

 

 

~

 

d~r

 

 

 

 

 

 

 

 

 

 

P

 

 

 

 

rot P~ (Mi)

 

 

 

`

 

 

 

 

 

~eni = lim

Hi

;

L

 

 

 

 

 

 

 

i!0

i

 

 

 

 

 

 

 

 

 

 

 

 

 

Ðèñ. 94

 

 

ãäå i площадь участка i.

 

 

Отсюда

 

 

 

 

 

 

rot P~ (Mi)

 

~eni i

 

P~

 

d~r

 

 

"i i ;

 

(3.85)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

`

 

 

 

 

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

где величина "i > 0 уменьшается с уменьшением диаметра ячейки i.

Обозначим " = max("i). Суммируя выражения (3.85) по всем ячейкам i, получаем

 

 

 

 

 

 

 

I

 

 

 

 

 

N

rot P~ (Mi) ~eni i

N

i

P~

 

" ;

(3.86)

 

 

 

d~r

X

 

 

 

X

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

N

 

 

 

 

 

 

 

 

 

i=1

 

 

i=1

 

`

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ãäå =

 

i=1 i площадь поверхности .

 

 

Ïðè

суммировании циркуляций в последней формуле каж-

P

 

 

 

 

 

 

 

 

 

дый из участков интегрирования, не относящийся к границе L, проходится дважды в противоположных направлениях (рис. 94), и соответствующие интегралы попарно взаимно уничтожа-

194

 

 

 

 

 

Глава 3.

ФУНКЦИИ ТОЧКИ

ются. Поэтому

 

I

 

 

 

I

 

 

 

 

N

 

 

 

 

 

 

 

X i

 

 

~

 

 

 

 

 

 

~

 

 

 

 

 

 

i=1

 

P d~r =

P d~r:

 

 

 

 

`

 

 

 

L

 

 

 

 

 

 

 

 

 

 

 

По определению потока векторного поля (3.47-3.48)

 

N

 

 

 

 

 

 

 

 

 

X

~

 

 

~

 

~

lim

rot P (Mi)

 

~eni i =

rot P

 

d :

N !1

 

 

 

 

 

ZZ

 

 

 

max j ij!0 i=1

 

 

 

 

 

Следовательно, увеличивая число участков разбиения N до бесконечности и уменьшая i и соответственно " до нуля, получим из (3.86)

ZZ I

~ ~ ~

rot P d = P d~r: (3.87)

L

Формула (3.87) выражает теорему Стокса: поток вихря век-

торного поля ~ через поверхность , ограниченную замкну-

P

тым контуром , равен циркуляции ~ по этому контуру, если

L P

компоненты векторного поля ~ вместе с их частными произ-

P

водными непрерывны на поверхности и на контуре L.

Из произвольности поверхности (имеющей границу L), фигурирующей в теореме Стокса, вытекает

С л е д с т в и е 1: поток вихря непрерывного поля через замкнутую поверхность равен нулю.

~

Компоненты вектора P в декартовой системе координат являются функциями координат x, y, z. Обозначим: Px = u(x; y; z), Py = v(x; y; z), Pz = w(x; y; z). Тогда формула Стокса в декартовой системе координат имеет вид

ZZ @y

@z cos +

@z

@x

cos +

@x

@y cos d =

 

@w

 

@v

 

 

@u

 

@w

 

 

@v

 

@u

 

 

 

 

 

= I

u dx + v dy + w dz;

(3.88)

L

Ÿ 8. Теорема Остроградского и связанные с ней формулы 195

ãäå cos = cos(~en; ~ex), cos =

cos(~en; ~ey ), cos

= cos(~en; ~ez )

косинусы единичного вектора нормали к по-

направляющие d

d

d

верхности .

Рассмотрим частный случай, когда поверхность является участком координатной плоскости Oxy. Тогда cos = cos = 0, cos d = dx dy элементарная площадка в плоскости Oxy, dz = 0, и из формулы (3.88) получаем

Ñ ë å ä ñ ò â è å 2. Ò å î ð å ì à Ã ð è í à.

ZZ

 

@v

 

@u

I

 

 

 

 

@x

 

@y

dx dy = L

u dx + v dy:

(3.89)

Здесь u и v функции двух переменных x и y, непрерывные вместе со своими частными производными.

Задачи 106. Доказать, что

II

x dy =

y dx = S;

L

L

где S площадь плоской фигуры, ограниченной кривой L.

Ÿ8. Теорема Остроградского и связанные с ней формулы

8.1.Теорема Остроградского. Пусть замкнутая поверхность, ограничивающая объ¼м V , M переменная точка

èç V , ~en единичный вектор внешней нормали к поверхности

~

~

. Рассмотрим вектор-функцию P

= P (M ) точки M , которая

непрерывна вместе со своими первыми производными в любой точке объ¼ма V и его границы .

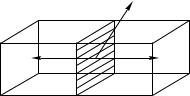
Мысленно рассеч¼м объ¼м V , например тремя системами взаимно ортогональных плоскостей, на N элементарных объ¼мов Vi (i = 1; : : : ; N ). Из определения (3.56) расхождения

~

векторного поля следует, что поток Ni вектора P через замкнутую поверхность, ограничивающую элементарный объ¼м Vi,

196

 

 

 

 

 

Глава 3.

ФУНКЦИИ ТОЧКИ

приближ¼нно равен

 

 

 

 

 

 

 

 

 

 

 

 

~

 

 

 

 

 

 

 

 

 

 

Ni div P (Mi) Vi ;

 

 

 

 

òî åñòü

div P~ (Mi) Vi

P~ d~

"i Vi;

 

 

 

 

 

(3.90)

 

 

 

 

 

ZZ

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ãäå M

i

некоторая точка из объ¼ма V

,

i

площадь по-

 

 

 

 

 

 

i

 

 

 

верхности, ограничивающей объ¼м Vi; величина "i òåì ìåíü-

ше, чем меньше максимальный из линейных размеров объ¼ма

Vi.

 

 

 

 

 

 

 

 

 

 

 

Суммируя неравенства (3.90) по всем участкам разбиения,

получаем

 

 

 

 

 

 

 

 

 

 

 

 

N

div P~ (Mi) Vi N

P~

d~ "V;

(3.91)

 

 

i=1

 

 

i=1 ZZ

 

 

 

 

 

 

 

X

 

 

X i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

N

 

 

 

 

 

 

 

ãäå " = max("i), V

= Pi=1

Vi.

Единичные векторы ~eni è

 

 

 

 

~

 

~eni 1 внешней нормали к по-

 

 

 

 

P

 

 

 

 

 

 

 

верхности, по которой грани-

 

 

 

 

 

 

чат друг с другом два со-

~eni

 

 

 

~eni 1

седних объ¼ма Vi 1

è Vi

 

 

 

(на рис. 95 эта пограничная

 

 

 

 

 

 

 

 

 

 

 

 

площадка заштрихована), на-

Vi 1

Vi

 

правлены в

 

противополож-

 

Ðèñ. 95

 

 

ные стороны.

 

 

 

 

 

 

 

 

 

 

 

 

 

~

~

 

вклад потока векторного поля

Поэтому P ~eni

= P ~eni 1 ;

через эту площадку в величины Ni è Ni 1 входит с разными

знаками. Следовательно, сумма потоков векторного поля через

поверхности i

всех составляющих объ¼м V

элементов Vi

равен потоку через поверхность :

 

 

 

 

 

X ZZ

 

ZZ

 

 

N

~

 

~

 

~

~

(3.92)

P d = P d :

i=1 i

 

Ÿ 8. Теорема Остроградского и связанные с ней формулы 197

Увеличивая число участков разбиения N до бесконечности одновременно уменьшая Vi è i, òàê, ÷òî

max Vi ! 0; и соответственно " ! 0;

получим из (3.92 - 3.91)

XN

lim

N !1

max j Vij!0 i=1

~

ZZ

~

~

div P

(Mi) Vi = P d :

Левая часть этого равенства есть интеграл по объ¼му V от дивергенции векторного поля. Окончательно имеем

ZZZ

V

~

ZZ

~

 

~

(3.93)

div P dV = P d :

Формула (3.93) выражает теорему Остроградского: интеграл по объ¼му от дивергенции векторного поля равен потоку поля через поверхность, ограничивающую этот объ¼м, если компоненты поля вместе с их частными производными непрерывны в объ¼ме и на поверхности.

Представим подынтегральные функции в формуле (3.93) в декартовой системе координат. В результате получим другую часто используемую форму теоремы Остроградского:

 

ZZZ @xx

+

@yy

+ @zz dV =

 

 

 

 

@P

 

@P

 

@P

 

ZZ

V

 

 

 

 

 

 

 

h

d

 

 

d

d i

 

 

 

 

= Pxcos(~en; ~ex)+Py cos(~en; ~ey )+Pz cos(~en; ~ez ) d :(3.94)

Координаты вектора независимые друг от друга функции, и следствием формулы (3.94) является равенство

ZZZ

 

i

ZZ

 

 

V

@f

 

d

(3.95)

 

@x

dV

= f cos(~en; ~ei)d ;

198

Глава 3. ФУНКЦИИ ТОЧКИ

где функция f непрерывна вместе со своей производной по координате xi внутри объ¼ма V и на поверхности , а xi одна из декартовых координат.

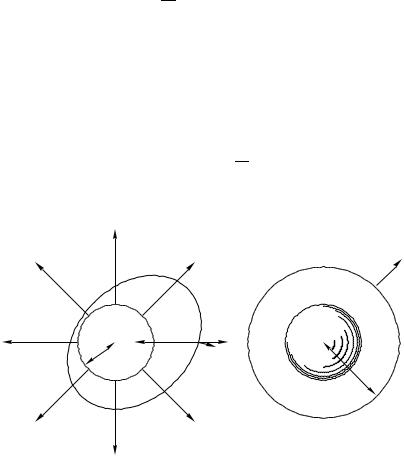
П р и м е р 96. Найд¼м поток кулоновского поля (3.64) через замкнутую поверхность , если начало координат не лежит на поверхности .

Случай 1. Начало координат т. O, относительно которой от- считывается радиус-вектор ~r, находится вне объ¼ма, ограниченного замкнутой поверхностью . Ранее (см. стр. 175) было показано, что кулоновское поле соленоидальное. Внутри области, охватываемой поверхностью , поле

~

~r

 

E = k

r3

(3:64)

удовлетворяет всем условиям теоремы Остроградского, и, следовательно, поток равен

ZZ

~

ZZZ

~

~

E d =

div E dV = 0:

V

Случай 2. Точка O находится внутри объ¼ма V , ограниченного поверхностью . В этой точке поле (3.64) имеет разрыв непрерывности. Выделим вокруг точки O сферический объ¼м радиуса R. На рис. 96 эта сфера показана штрихованной линией. В объ¼ме, ограниченном поверхностью и поверхностьюR, векторное поле (3.64) удовлетворяет всем условиям теоремы Остроградского. Поэтому

ZZ

~

Z Z

~

~

 

ZZZ

~

~

 

 

 

E d + E d R =

V

div E dV = 0;

 

 

R

 

 

 

 

откуда

 

ZZ

 

 

Z Z

 

 

 

~

 

~

 

 

~

 

 

~

 

 

E d = E d R :

 

 

 

 

 

R

 

 

Все точки сферы R находятся на одном и том же расстоя-

 

 

 

~

 

~

3

в каждой точке поверх-

нии R от точки O; вектор E = kR=R

ности R направлен по нормали к последней (под углом 180 к

Ÿ 8. Теорема Остроградского и связанные с ней формулы 199

 

 

~

2

. Площадь

направлению единичного вектора ~eR) è jEj = k=R

 

поверхности сферы равна 4 R2, следовательно,

 

 

Z Z

~

Z Z

 

 

~

~

 

 

E d R = E ~eRd R = 4 k;

 

 

R

 

R

 

 

и поток кулоновского поля через произвольную поверхность равен

ZZ

~r

 

(3.96)

k r3

~end = 4 k:

С л е д с т в и е 1. Для напряж¼нности электрического поля точечного заряда Q постоянная k для вектора (3.64) равна k = Q=4 "0 (в вакууме в СИ), поэтому поток напряж¼нности электрического поля точечного заряда через любую поверхность, охватывающую заряд, равна

 

ZZ

 

 

0

 

 

 

~

 

Q

 

(3.97)

 

E ~end =

"

 

;

ãäå "0 электрическая постоянная.

 

 

 

 

 

 

 

 

 

~

 

 

 

 

 

 

E

 

 

 

 

 

 

A

 

~eR

~

 

 

 

 

R

 

E

 

 

 

 

 

 

 

 

 

 

O

~en

 

 

 

r

 

 

 

 

 

 

 

R

 

 

 

 

 

 

 

 

 

 

 

 

Ðèñ. 96

Ðèñ. 97

200

Глава 3. ФУНКЦИИ ТОЧКИ

Ñл е д с т в и е 2. З а к о н Г а у с с а: поток напряж¼нности электрического поля через любую замкнутую поверхность равен сумме зарядов, охватываемых этой поверхностью, дел¼нной на электрическую постоянную. Для доказательства этого утверждения достаточно учесть формулу (3.97) и свойство потока векторного поля поток суммы полей через некоторую поверхность равен сумме потоков каждого из складываемых полей через ту же поверхность.

Ñл е д с т в и е 3. П о л е з а р я ж е н н о г о ш а р а. Рассмотрим

~

электрическое поле E в некоторой точке A (рис. 97) где-то снаружи сферы, наполненной электрическим зарядом, плотность распределения которого радиальная. В этом случае напряж¼н-

~

ность электрического поля E всюду направлена прямо от цен-

~

тра сферы (для положительного заряда). Поток поля E через воображаемую сферическую поверхность, концентрическую со сферой зарядов и проходящей через A, равен E4 r2, а по закону Гаусса Q="0, где Q суммарный заряд сферы. Значит,

1 Q

E = 4 "0 r2 ;

напряж¼нность электрического поля заряженной сферы точно такая же, как и у точечного заряда Q.

С л е д с т в и е 4. С и л а т я г о т е н и я ш а р а с р а д и а л ь- н о й п л о т н о с т ь ю (r) р а с п р е д е л е н и я м а с с ы. Напряж¼нность гравитационного поля, создаваемого материальной точкой массой mi в некоторой точке A сила, действующая со стороны этого поля на материальную точку единичной массы, помещ¼нную в точку A, является примером кулоновского поля (3.64), в котором постоянная k выражается через гравитационную постоянную и массу mi: k = mi. Поэтому напряж¼нность гравитационного поля шара массой

XZZZ

M = mi = (r) dV

iV

определяется аналогично электрическому полю заряженного шара, и сила, действующая со стороны такого шара на мате-

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности