Беляев Ю.Н. Введение в векторный анализ

которого, направленная по вектору ~eb ~ec; делит угол A пополам.

Составим векторное уравнение биссектрисы угла A, как прямой, проходящей через точку A(~rA ) параллельно вектору ~eb ~ec (см. формулу (1.10)). Получим

Ðèñ. 16

Точка пересечения этих биссектрис должна удовлетворять обоим уравнениям (1.18) и (1.19). Значит, должно выполняться

Исключая из этой формулы вектор ~a с помощью замены ~a =

~

b ~c, после элементарных преобразований получим:

~

Векторы b и ~c не коллинеарны друг другу, поэтому равен-

~

ство (1.20) возможно только, если множители при b и ~c тождественно равны нулю. Следовательно, должны выполняться следующие соотношения

Подставляя выражение (1.21) в формулу (1.18) (или (1.19)), получим значение радиус-вектора точки пересечения биссектрис углов A и B

Непосредственной проверкой можно убедиться, что точка пересечения биссектрис углов B и C тоже определяется формулой (1.22). Таким образом, все три биссектрисы пересекаются в одной точке, радиус-вектор которой выражается формулой (1.22).

2.2. Перемещение, скорость и ускорение материальной точки. Одной из основных моделей материальных тел, движение которых исследует механика, является материальная точка тело, размерами которого в условиях данной задачи можно пренебречь и считать все его вещество сосредоточенным в одной геометрической точке. Напомним некоторые из основных положений механики материальной точки.

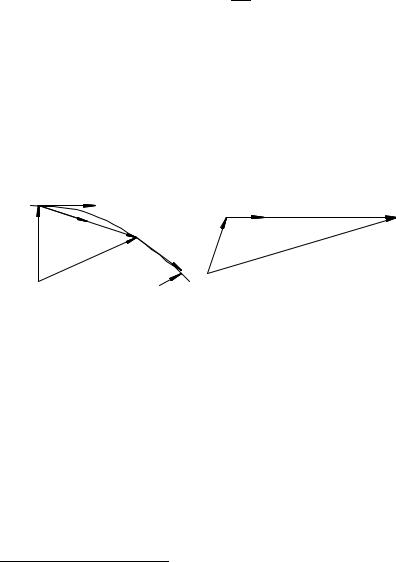
При движении материальной точки (м.т.) ее радиус-вектор ~r описывает в пространстве кривую, называемую траекторией движения. Пусть в начальный момент времени t0 материальная точка (м.т.) находилась в положении M0(~r0), определяемом радиус-вектором ~r0, а в момент времени t > t0 в положении M (~r). Вектор ~r, проведенный из начального положения м.т. M0 в конечное M , называется перемещением м.т. за времяt = t t07. По правилу сложения векторов (рис. 17) ~r = ~r ~r0, т.е. перемещение это изменение (или приращение) радиусвектора точки за время t.

Средней скоростью движения м.т. ~vcp называется отношение перемещения ~r к интервалу времени t

это вектор, направленный в ту же сторону, что и перемещение~r, величина которого в общем случае зависит от выбора момента времени t0 и величины интервала t.

Для фиксированного момента t0 при уменьшении интервала времени t будет уменьшаться и перемещение ~r. При этом отношение ~r= t стремится к некоторому вектору ~v0, который

7 прописная греческая буква "дельта", это не множитель, а символ, и t не произведение на t. Символ заменяет здесь слово "прираще-

ние"(другое значение этого обозначения да¼тся в примечании на стр.178); запись t читается как "дельта тэ"или "приращение времени".

При неравномерном движении м.т. быстроту изменения скорости характеризуют ускорением ~a. Рассмотрим р а в н о у с к о- р е н н о е д в и ж е н и е. Это такое движение, при котором равные изменения скорости происходят за равные промежутки времени. Обозначим скорость м.т. в начальный момент времени t0 = 0 вектором ~v0, а ~v скорость в момент времени t, тогда ~a = (~v ~v0)=t: Из этой формулы, зная ускорение м.т., можно найти ее скорость в любой момент времени

При равноускоренном движении положение м.т. в пространстве описывается радиус-вектором

Согласно условию компланарности векторов (1.3) и законам (1.24) и (1.25), скорость м.т. ~v и перемещение ~r ~r0 лежат в одной плоскости с постоянными векторами ~v0 и ~a. Следовательно, равноускоренное движение м.т. является плоским.

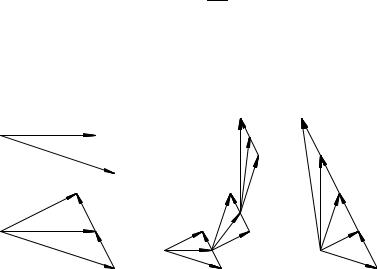
Рис. 19 П р и м е р 8. Материальная точка, начиная равноускорен-

ное движение в момент t = 0 из положения M0 c начальной скоростью ~v0, в момент времени t = 1 попадает в положение M1. Полагая масштабы построения единиц расстояний и скоростей на рис. 19a одинаковыми, найти графическим построением положения м.т. в моменты t = 2 и t = 3.

!

Вектор M0M1 это перемещение м.т. ~r01 за первый интервал

!

времени t = 1. С другой стороны по условию задачи M0M1 численно равен средней скорости движения за этот интервал времени ~vcp1 (см. рис. 19b). Следовательно, вектор, проведенный

из конца ~v0 в точку M1; есть ~at=2. Увеличивая его в два раза,

!

получаем вектор A0A1 = ~at.

Теперь, выполняя сложение согласно формуле (1.24) по правилу треугольника, находим скорость м.т. ~v1 в момент времени t = 1, как это представлено на рис. 19b.

Дальнейшее графическое решение задачи показано на рис.

19c, масштаб которого в два раза меньше, чем рис. 19a; b: Из

! !

точки M1 строим вектор M1A2 = M0A1 = ~v1, прибавляем к

! !

нему по правилу треугольника A2A3 = A0A1 = ~at. В результате

!

находим скорость ~v2 = M1A3: Середина отрезка A2A3 åñòü M2положение м.т. в момент времени t = 2.

Аналогичным образом (см. рис. 19c) находится положение м.т. M3 в момент времени t = 3 и могут быть найдены последующие (с единичным временным интервалом) положения м.т.

Для нахождения скоростей м.т. в моменты времени t = 1; 2; 3 : : : достаточно прибавить к ~v0 соответственно векторы ~at; 2~at; 3~at и т.д. (см. рис. 19d). Заметим, что если начала векторов скорости для любого момента времени привести к общему на- чалу, то концы этих векторов в соответствии с формулой (1.24) опишут прямую линию.

2.3. Понятие силы. Воздействие на материальную точ- ку (м.т.) со стороны других тел, в результате которого может происходить изменение движения м.т., называется механиче- ским. Мерой механического воздействия является сила.

~

Сила F это вектор, который на рисунках изображается в виде направленного отрезка, отложенного от материальной точки в направлении механического воздействия на нее со

вание величин, каждая из которых получается из общего члена суммы kmj (~rj ~r), когда индекс суммирования j пробегает все целые значения от наименьшего числа j, указанного снизу знака P; до наибольшего значения, указанного над знаком P : Â

~

формуле для равнодействующей R суммирование проводится от j = 1 до j = n . Такой способ записи операции суммирования очень удобен, когда слагаемых много, и в дальнейшем неоднократно будет нами использоваться.

Преобразуем формулу для равнодействующей следующим образом. Раскроем скобки в правой части последнего равенства и объединим слагаемые, содержащие радиус-вектор ~r точки M . Получим

Центром масс m1; m2; : : : ; mn называется точка, положение которой определяется радиус-вектором:

Используя это определение вектора ~rc , можно переписать выражение для равнодействующей следующим образом:

~

R = k(m1 + + mn)(~rc ~r):

Последняя формула означает, что равнодействующая направлена к центру масс и пропорциональна их сумме. Из этой же формулы сразу вытекает, что точка M будет в равновесии, если ~r = ~rc, т.е. когда точка M находится в центре масс

m1; m2; : : : ; mn.

Задачи

13.Доказать, что если диагонали четырехугольника делят друг друга пополам, то четырехугольник есть параллелограмм.

Указание. Используя формулу (1.15), выразить радиус-вектор точки пересечения диагоналей через радиус-векторы противолежащих вершин четырехугольника.

14.Найти центр масс трех материальных точек M1(~r1), M2(~r2), M3(~r3), в которых сосредоточены массы m1; m2; m3,

причем ½сложенные\ и ½умноженные\ элементы должны удовлетворять следующим условиям:

Говоря о ½сложении\ элементов линейного пространства и об ½умножении\ их на числа, следует помнить, что эти действия требуют своего определения в каждом конкретном случае.

Для сравнения в формулах (1.29)-(1.36) рядом со свойствами линейного пространства даны соответствующие свойства векторов. Нетрудно заметить, что векторы удовлетворяют всем свойствам линейного пространства. Именно поэтому в общем случае элементы линейного пространства также называют векторами. Эти векторы мы будем отмечать полужирным шриф-

~

том a, b, c; : : :, отличая тем самым их от векторов ~a; b; ~c; : : :, геометрическими образами которых являются направленные отрезки, складываемые по правилу параллелограмма (треугольника).

Привед¼м ещ¼ ряд примеров линейных пространств.

3.1.Примеры линейных пространств.

П р и м е р 10. Если на прямой линии заданы начало координат, единица масштаба и направление, то каждой точке этой

30 Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ

прямой можно сопоставить число (положительное, если точка лежит от начала координат в направлении оси, и отрицательное в противном случае). Эти числа образуют множество действительных чисел R линейное пространство, в котором операцией сложения является обычное арифметическое сложение. Нулевой элемент число 0.

П р и м е р 11. М н о ж е с т в о к о м п л е к с н ы х ч и с е л C: Выберем на плоскости прямоугольную систему координат.

Тогда каждая точка z плоскости однозначно характеризуется парой действительных чисел: абсциссой a и ординатой b. Условимся записывать точки плоскости через z = (a; b).

Пары действительных чисел a и b, соответствующие всем точкам плоскости, называется комплексными числами z = (a; b), если они подчиняются следующим правилам сложения и умножения:

суммой комплексных чисел z1 = (a1; b1) è z2 = (a2; b2) является комплексное число z = (a; b), у которого a = a1 + a2 è b = b1 + b2, òî åñòü

z 1 + z 2 = (a1; b1) + (a2; b2) = (a1 + a2; b1 + b2); (1 )

Плоскость, на которой изображаются комплексные числа, называется плоскостью комплексного переменного.

Очевидно, что два комплексных числа z 1 = (a1; b1) è z 2 = (a2; b2) равны друг другу, т.е. им соответствует одна точка на плоскости комплексного переменного, в том и только в том слу- чае, если a1 = a2 è b1 = b2.

Разностью двух комплексных чисел z 1 = (a1; b1) è z 2 = (a2; b2) будет такое z = (a; b), что

z 1 = z 2 + z ; èëè (a1; b1) = (a2; b2) + (a; b):