
Беляев Ю.Н. Введение в векторный анализ
.pdf
Ÿ 5. Сложение движений |
131 |
Задачи.
73. Показать, что угловую скорость !~ твердого тела можно выразить через базисные векторы ~ex; ~ey ; ~ez связанной с телом декартовой системы координат OXY Z в виде
|
d~e |
|
d~e |
|
d~e |
|
|
!~ = |
y |
~ez ~ex + |
z |
~ex ~ey + |
x |
~ey ~ez : |
(2.99) |
dt |
dt |
dt |
|||||
74. Показать, что при сложном движении точки имеют ме- |
|||||||
сто следующие соотношения: |
_ |
|
|
_ |
|||
1) ~vr = ~ar + ~ac=2; |
2) ~ve = |
||||||
~ae + ~ac=2:
75.Катер плывет прямолинейно со скоростью v1: Второй катер плывет со скоростью v2 под углом к направлению движения первого. Найти величину и направление скорости второго катера, определяемые наблюдателем, находящимся на палубе первого.
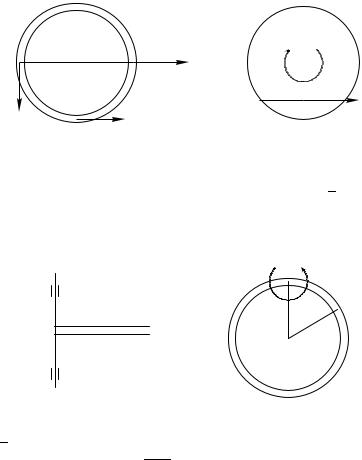
76.Точка A движется по ободу диска радиуса R согласно уравнению OA = c1t: Диск вращается вокруг оси, проходящей через т. O перпендикулярно плоскости диска (рис. 74) по за-
êîíó ' = c2t: Найти абсолютную скорость т. A в положении, показанном на рисунке, если c1 = 0:2 ì/ñ; c2 = 2 c 1; R = 0:3 ì:
O |
O |
Y |
|
|
|
|
|
P |
|
|
' |
R |
|
A |
|
|
|
|
A |
|
Ðèñ. 74 |
Ðèñ. 75 |
|
|
X |
|
77. Стержень OA вращается в плоскости OXY вокруг т. O против часовой стрелки (рис. 75). По стержню скользит колеч- ко P: Пренебрегая размерами колечка, найти его абсолютную
скорость и абсолютное ускорение в момент времени t = 1 c; если p
' = C sin 4 t; OP = Bt2; ãäå C = 4 10= ; B = 2 ì/ñ2:
78.Решить предыдущую задачу при условии, что ' =
Bt; OP = OA sin Bt; B = 2 c 1; OA = 0:1 ì; 0 t =2:
79.Частицы жидкости, принимаемые за материальные точ- ки, движутся со скоростью vr = 0:06 м/с в тонкой трубке, име-
132 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
ющей форму окружности радиуса R = 0:1 м (см. рис. 76). Трубка равномерно вращается вокруг оси AB с угловой скоростью ! = 0:4 рад/с: Определить абсолютное ускорение частиц жидкости в положениях A и C:
A |
|
B |
O |
|
|
|
|
|
|
|
!~ |
~vr |
C |
|
A |
|
|
||
|
|
~vr |
~vr |
|
Ðèñ. 76 |
|
Ðèñ. 77 |
80. |
p |
|
|
М.т. движется с относительной скоростью vr = 0:1 2 |
|||
t(м/с) по хорде диска, вращающегося вокруг оси O; перпенди- p
кулярной плоскости диска, с угловой скоростью ! = 2 рад/с: В момент времени t = 2 c м.т. находится в положении A (рис. 77). Определить абсолютное ускорение м.т. в этот момент времени, если OA = 0:6 м:
O1 |
O |
|
|
|
A |
A0 |
A |
Ðèñ. 78 |
Ðèñ. 79 |
|
|
O |
|
81. Трубка вращается вокруг оси OO1 с угловой скоростью p
! = 2 рад/с: Маленький шарик A движется вдоль трубки (см. p
рис. 78) по закону A0A = 0:72 t2(м): Найти модуль абсолютного ускорения шарика в момент времени t = 1 с:
82. Полое кольцо (рис. 79) радиуса R = 2= 2 м вращается по закону ' = t2=4 вокруг оси O; перпендикулярной плоскости кольца. По кольцу движется м.т. A по закону OA = t2= : Найти модуль абсолютного ускорения м.т. в момент времени t = 1 с:

Глава 3
ФУНКЦИИ ТОЧКИ
Ÿ1. Скалярное поле
1.1.Поверхность уровня скалярного поля. Если каждой точке M из области поставлено в соответствие определ¼нное значение некоторой скалярной величины U = U (M ), то говорят, что в области задано скалярное поле этой величи- ны. Например, температура воздуха в различных точках пространства образует поле температур, а значение потенциала то- чечного заряда поле электрического потенциала.
Совокупность точек M; в которых скалярная функция U (M ) принимает одинаковые значения, называется поверхностью уровня, или изоповерхностью. Уравнение поверхности уровня, проходящей через точку (x0; y0; z0), имеет вид
U (x; y; z) = U (x0; y0; z0):
П р и м е р 53. Рассмотрим поверхности уровня электростатического потенциала точечного заряда q
' = qr ;
где r расстояние от точечного заряда q до т. M: Уравнение поверхности уровня данного поля (е¼ ещ¼ называют эквипотенциальной) находим из условия '(r) = const; откуда r = const; т.е. поверхностями уровня электростатического поля '(r) точечного заряда q являются сферы, концентрические относительно заряда.
В случае, когда скалярное поле задано на плоскости, эквипотенциальные поверхности поля превращаются в ее линии уровня.
133
134 Глава 3. ФУНКЦИИ ТОЧКИ
П р и м е р 54. Для скалярного поля U (M ) = x2+4y2 (x; y декартовы координаты точки M ) линии уровня определяются
уравнением |
|
|
|
|
|
x2 + 4y2 = C2; èëè |
x2 |
+ |
y2 |
= 1: |
|
C2 |
(C=2)2 |
||||
|
|
|
Последнее равенство есть уравнение эллипсов с полуосями a =
C è b = C=2:
Максимальная наглядность графического изображения скалярного поля с помощью поверхностей уровня достигается, если эти поверхности проводятся для равноотстоящих значений функции. Места сближения двух последовательных изоповерхностей указывают на быстрое изменение здесь функции.
1.2.Дифференцируемое скалярное поле. Возьмем
две точки M и M 0; принадлежащие и определяемые радиус-
|
|
|
|
~0 |
соответственно. |
|
|
векторами ~r и r |
|
|
|||||
Используем следующие обозначения: |
|
|
|||||
|
~0 |
~r |
|
0 |
, иначе |
||
~r = r |
вектор, провед¼нный из т.M в т.M |
||||||
говоря, ~r = M!M 0; |
|
|
|||||
` = j |
~r |
расстояние между точками M и M 0; |
|
|
|||
|
~rj |
|
0 |
|
|
||
~e` = |
|
|
|
единичный вектор в направлении т. M |
; |
|
|
` |
|
|
|||||
U = U (M 0) U (M ) приращение скалярного поля. |
|||||||
Скалярное поле U (M ) называется дифференцируемым в т. |
|||||||
M области ; если для любого ~r = ` ~e` приращение поля U в т. M может быть представлено в виде
U = ! |
|
~r + (`); |
|
(3.1) |
||
G |
|
|
|
|||
G не зависит от ~r; а величина при ` |
|
0 ñòðå- |
||||
где вектор ! |
|
|
|
! |
|
|
мится к нулю (`) ! 0 быстрее, чем `; т.е. |
|
|||||
|
|
|||||
lim |
(`) |
= 0: |
|
(3.2) |
||
|
|
|||||
`!0 |
|
` |
|
|
|
|
Линейная часть приращения скалярного поля есть диффе- |
||||||
ренциал скалярного поля |
|
|
|
|
|
|
~ |
|
|
|
(3.3) |
||
dU = G d~r; |
|
|||||

Ÿ 1. Скалярное поле |
135 |
ãäå d~r = ~r.
Покажем, что если поле U (M ) дифференцируемо, то вектор
~ |
|
|
|
|
|
|
|
|
|
|
|
G определяется формулой (3.1) единственным образом. |
|||||||||||
Предположим, что существуют два представления U в т. |
|||||||||||
M : |
|
|
|
|
|
|
|
|
|
|
|
! |
|
~r + 1(`); |
|
è |
|
|
! |
~r + 2(`): |
|||
U = G1 |
|
|
U = G2 |
||||||||
Тогда |
|
! |
! |
|
|
|
|
|
|
|
|
|
|
~r = 2(`) |
1(`); |
||||||||
|
|
(G1 |
G2) |
|
|
||||||
èëè |
|
|
|
|
|
|
|
2(`) 1(`) |
|
||
|
|
(G1 |
G2) |
|
~e |
` |
= |
: |
|||
|
|
! |
! |
|
|
|
` |
|
|
||
Последнее равенство должно выполняться при любом `; в частности при ` ! 0: В соответствии с условием (3.2) для лю-
áîãî ~e`
! !
(G1 G2) ~e` = 0;
! !
откуда G1 = G2; что и требовалось доказать.
1.3. Производная по направлению. Рассмотрим отношение приращения скалярного поля U , которое функция U приобретает при смещении из т. M в т. M 0 в направлении ~e`, к величине смещения `
U |
= |
U (M 0) U (M ) |
= |
U (~r + `~e`) U (~r) |
: |
|
` |
||||||
|
` |
|
` |
|
Если существует предел этого отношения при ` ! 0, то он называется производной функции U по направлению ~e`
@U |
|
lim |
U |
: |
(3.4) |
|
@` |
` |
|||||
`!0 |
Если скалярное поле U дифференцируемо в точке M , то существует производная от U по любому направлению `, которая в соответствии с формулами (3.1) и (3.2) может быть представлена в виде
@U |
= |
! |
|
|
` |
|
(3.5) |
@` |
|
|
|||||
|
|
G |
|
~e |
|
: |

136 |
Глава 3. ФУНКЦИИ ТОЧКИ |
Ñ â î é ñ ò â à |
ï ð î è ç â î ä í î é ï î í à ï ð à â ë å í è þ, íåïî- |
средственно вытекающие из е¼ определения:
1)производная вдоль поверхности уровня равна нулю;
2)производная суммы полей равна сумме производных
@(U1 + U2) |
= |
@U1 |
+ |
@U2 |
; |
(3.6) |
|
@` |
@` |
@` |
|||||
|
|
|
|
3) производная скалярного поля U('1; '2), которое является функцией дифференцируемых скалярных полей '1(M ) è '2(M ), вычисляется по формуле
@U ('1; '2 ) |
= |
dU @'1 |
+ |
dU @'2 |
: |
(3.7) |
|||||
|
|
|
|
|
|
|
|||||
@` |
d'1 @` |
d'2 @` |
|||||||||
|
|
|
|
||||||||
Зная производную @U@` по любому направлению ~e`, можно вычислить значение функции U в точке M 0 с точностью до членов второго порядка малости
U (M 0) U (M ) + @U@` ` :
1.4.Геометрический смысл градиента. По формуле
(3.5) производная по направлению |
@U |
максимальна, когда век- |
||
|
|
|
@` |
|
òîð ~e |
` |
направлен в ту же сторону, что и G : Следовательно, век- |
||
|
|
|
! |
|
G ; определяемый формулой (3.1), направлен в сторону мак- |
||||
òîð ! |
|
|
|
|
симального возрастания поля U > 0 перпендикулярно поверх- |
||||
ности уровня ( U = 0) поля U в точке M: Максвелл ввел для |
||||
этого вектора термин ½градиент\ |
1 и обозначение grad U (M ), |
|||
которое читается как ½градиент скалярного поля U в т. M \. Таким образом,
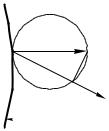
В соответствии с определением (3.5), производная скалярного поля по направлению ~e` есть проекция градиента этого поля на данное направление. Соотношение (3.5) позволяет находить производную скалярного поля по направлению простым геометрическим построением (см. рис. 80).
1От латинского слова gradior идти вперед, расти.
Ÿ 1.
M
137
Проведем через точку M поверх-
ность уровня U = U (M ) и перпен-
!
дикулярно к ней строим вектор G = grad U (в направлении возрастания по-
ля U ). Далее строим сферу, для кото-
!
рой G является диаметром. Обозна-
~
чим точку пересечения вектора `, про-
Pведенного из M в M 0, с поверхностью
|
M 0 |
сферы буквой P . По построению, от- |
|
U =U (M ) |
|
G |
|
|
|
|
|
|
|
резок M P есть проекция вектора ! |
|
Ðèñ. 80 |
~ |
@U |
|
|
|
на направление `, т.е. M P = |
@` . |
Если в каждой точке M области выполняются соотношения (3.1-3.2), скалярное поле U (M ) дифференцируемо в области; и в каждой точке этой области существует градиент скалярного поля grad U:
П р и м е р 55. Используя определение (3.3), найти градиент скалярного поля U = j~c ~rj2, где ~c постоянный вектор.
Решение. Вычислим дифференциал данного поля dU = dj~c ~rj2 = d(~c ~r)2 = 2(~c ~r) (~c d~r):
Преобразуем полученное выражение, для этого обозначим ~c ~r = ~a и используем независимость смешанного произведения от циклической перестановки множителей
~a (~c d~r) = d~r (~a ~c) = d~r [(~c ~r) ~c]:
Следовательно,
dU = d~r 2[(~c ~r) ~c]:
Сравнивая это выражение с формулой (3.3), находим
grad j~c ~rj2 = 2[(~c ~r) ~c] = 2c2~r 2(~r ~c)~c:
1.5. Градиент суммы. Пусть в области даны два дифференцируемых скалярных поля U1 è U2. Тогда в любой точке этой области существуют производные по направлению:
@U1 |
= grad U1 ~e` ; |
@U2 |
= grad U2 ~e` ; |
(3.8) |
@` |
@` |
138 |
|
Глава 3. |
ФУНКЦИИ ТОЧКИ |
и суммарное поле U = U1 + U2 тоже дифференцируемо, прич¼м |
|||
|
@U |
= grad U ~e` : |
(3.9) |
|
|
||
@` |
|||
Используя свойство (3.6) и формулы (3.8) и (3.9), получаем grad U ~e` = (grad U1 + grad U2) ~e` :
Это равенство должно выполняться для любого ~e` , следовательно,
grad U = grad U1 + grad U2 ; |
(3.10) |
градиент суммы полей равен сумме градиентов.
Пусть даны поверхности уровня функции U1 и функции U2, построенные для равноотстоящих значений, соответственно U1 = U10 n è U2 = U20 n :
U1 = : : : ; |
U10 2 ; |
U10 ; |
U10; |
U10 + ; |
U10 + 2 ; |
: : : ; |
U2 = : : : ; |
U20 2 ; |
U20 ; |
U20; |
U20 + ; |
U20 + 2 ; |
: : : |
На рис. 81 показаны линии уровня, соответствующие сече- ниям этих поверхностей плоскостью чертежа.
Значению '0 cуммарного скалярного поля ' = U1 + U2 соответствуют точки пересечений линий
U1 = U10 ; è U2 = U20 ;
U1 = U10 + ; è |
U2 = U20 ; |
|
U1 = U10 ; |
è |
U2 = U20 + ; |
: : : |
|
: : : |
Значения '0 принадлежат точкам пересечения линий
U1 = U10 + ; è U2 = U20 2 ;
U1 = U10 ; è U2 = U20 ;
U1 = U10 ; è |
U2 = U20 ; |
|
U1 = U10 2 ; |
è |
U2 = U20 + ; |
: : : |
|
: : : |

Ÿ 1. Скалярное поле |
139 |
На рис. 81 штрихованными линиями приближ¼нно показаны следы поверхностей уровня ' = '0, ' = '0 è ' = '0 2 , это диагональные кривые криволинейных четыр¼хугольников, образованных линиями уровней U1 = const è U2 = const.
'0
'0 2
grad '(M )
|
|
|
|
grad U2 (M ) |
|
|
|
|
|
'0 |
|
|
grad U1(M ) |
M |
|
||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
grad U2(N ) |
|
|
|
|
|
N |
|
|
|
|
|
grad U1(N ) |
0 |
|
|
|
|
grad (N ) |
|
U20 + |
|
|
|
0 + U10 |
2 |
|
|
|
|
||
|
U20 |
|
|
|
|
|
U20 |
|
U10 |
|
|
|
|
|
|
||
|
|
|
|
U10 |
|
Ðèñ. 81 |
U20 |
2 |
U10 |
+ |
|
|
|
|
|||
|
|
|
|
|
|
Нетрудно заметить, что другая серия диагональных кривых данных криволинейных четыр¼хугольников есть линии уровня для разности скалярных полей. На рис. 81 пунктирными линиями показаны следы поверхностей уровня поля = U1 U2 для тр¼х значений 0 = U10 U20 , 0 = U10 U20 è
0 + = U10 U20 + .
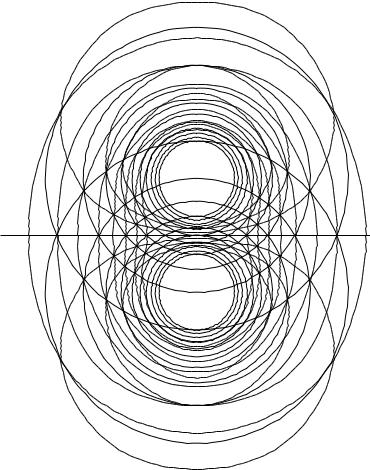
П р и м е р 56. Эквипотенциальные поверхности электростатического поля двух единичных точечных зарядов.
Две системы концентрических окружностей на рис. 82 изображают линии уровня потенциалов двух точечных зарядов, на-
140 |
Глава 3. ФУНКЦИИ ТОЧКИ |
ходящихся в точках A и B. Разность потенциалов между двумя соседними линиями уровня составляет 1=12 единицы потенциала (системы СГСЭ).
3
21
A
4
B
5
67
Ðèñ. 82
Если в точках A и B находятся отрицательные заряды, линии уровня суммарного поля схематично изображают штрихованные кривые (проведены для значений от 5=12 до 1 с интервалом 1=12 единиц через соответствующие точки пересечений окружностей).
Если один заряд отрицательный, а другой положительный, линиям уровня суммарного поля соответствуют пунктирные
