Беляев Ю.Н. Введение в векторный анализ

Ÿ 4. Криволинейные ортогональные системы координат 111

Решение. Согласно формуле (2.73) и условию задачи можно составить следующую систему дифференциальных уравнений, описывающих движение м.т.:

(

Преобразуем второе уравнение с учетом первого:

11

'= cr2 = c r:

Пусть в начальный момент времени t = 0 полярные координаты м.т. были: r(0) = r0; '(0) = '0: Тогда, интегрируя последнее уравнение

находим уравнение траектории м.т. в полярной системе координат:

r = r0 + c(' '0):

По формуле (2.74) находим радиальную составляющую ускорения

q

Следовательно, ускорение м.т. a = a2r + a2' = jar j:

Задачи 68. Найти траекторию м.т. при плоском движении, если

угол между радиус-вектором ~r и скоростью м.т. ~v равен = const:

112 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА

69. Найти траекторию м.т. при плоском движении, если

d

v = const; (~v; ~x) = ct (c = const > 0) и в начальный момент времени t = 0: координаты точки равны x = 0; y = 0:

70.Доказать, что если при плоском движении м.т. r2' = const; òî ~a k ~r:

71.Найти проекции скорости и ускорения м.т. в цилиндри- ческой системе координат: q1 = r; q2 = '; q3 = z.

72.Найти проекции скорости и ускорения м.т. в сфериче-

ской системе координат q1 = r; q2 = ; q3 = '.

Ÿ5. Сложение движений. Приложение к кинематике

Кинематика рассматривает движение тел с геометрической точки зрения без учета причин, вызывающих изменение их движений. Основными инструментами такого рассмотрения являются скорость и ускорение, определяемые соответственно формулами (2.2) и (2.3). Кинематические элементы движения м.т. зависят от выбора системы отсчета тела (или системы тел), с которой связана система координат, и от системы координат. В п р и м е р е 39 для рассмотрения скорости и ускорения использована декартовая система координат, а в разделе 4.2. получены формулы скорости и ускорения применительно к произвольной ортогональной системе координат. Если в первом случае базисные векторы системы координат остаются одинаковыми для всех точек пространства, то в общем случае криволинейной системы координат ориентация базиса меняется от точки к точке.

Предположим, в системе отсчета O0X10 X20 X30 ; в которой нас интересует движение м.т., это движение представляется более сложным, чем в системе OX1X2X3; движущейся относительно O0X10 X20 X30 : Задача, к решению которой мы сейчас приступаем, состоит в следующем. Нужно выразить ½сложное\ движение м.т. в системе O0X10 X20 X30 через более простые движения м.т. относительно системы OX1X2X3 и системы OX1X2X3 относительно O0X10 X20 X30 :

5.1. Перемещение системы отсч¼та. Угловая скорость. Выберем в качестве движущейся системы отсчета абсолютно твердое тело систему материальных точек, расстояния между которыми остаются неизменными при любых внешних воздействиях. Взаимная ориентация осей связанной с этим телом системы координат OX1X2X3 не изменяется в те- чение времени.

Перемещение системы отсчета, при котором связанные с ней базисные векторы системы координат остаются все время параллельными самим себе, называется поступательным.

Вращательное перемещение (вращение) одной системы от- счета относительно другой движение, при котором все точ- ки некоторой прямой, зафиксированной относительно первой системы, остаются неподвижными и относительно второй. Эта прямая называется осью вращения.

Т е о р е м а (Эйлера). Любое перемещение абсолютно тв¼рдого тела и, следовательно, связанной с ним системы координат OX1X2X3, может быть осуществлено поступательным перемещением и вращением вокруг оси, проходящей через центр O:

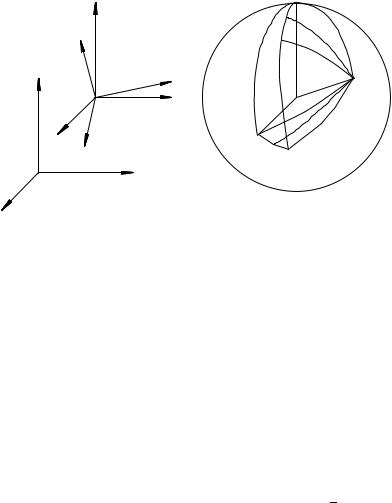
Доказательство. Обозначим единичные базисные векторы системы OX1X2X3 через ~e1; ~e2; ~e3: Рассмотрим перемещение системы OX1X2X3 из положения 1; где она задается единичными векторами ~ei(1)(i = 1; 2; 3), в положение 2; в котором направления координатных осей определяются единичными векторами

~ei(2) (i = 1; 2; 3) (ðèñ. 64a).

Очевидно, параллельным переносом системы OX1X2X3 можно переместить ее начало т. O из положения O(1) в положение O(2): При этом система координат займет промежуточное положение 20; в котором ~ei(20) = ~ei(1) (i = 1; 2; 3): Покажем теперь, что из положения 20 систему можно перевести в положение 2 вращательным перемещением.

Опишем вокруг начала координат O сферу единичного ра-

соединяющие концы векторов ~e3 è ~e1 в положениях 2 и 20 ñî-

перпендикулярно им проведем дуги больших кругов (на рис.

114 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА

64b они показаны штрихованными линиями), которые пересекутся в некоторой точке C:

клонные, одинаково удаленные от оснований сферических перпендикуляров (по построению). Взаимная ориентация базисных векторов ~e1; ~e2; ~e3 при движении системы OX1X2X3 не меняет-

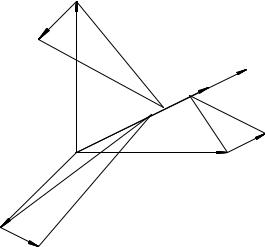
Сферический треугольник A0B0C может быть совмещен с равным ему треугольником ABC поворотом на угол 6 A0CA вокруг т. C: В этом случае ~e3(20) перейдет в ~e3(2) è ~e1(20) â ~e1(2): Взаимная ориентация базисных векторов изменяться не может, поэтому базисный вектор ~e2 также перейдет из положения 20 в 2: Указанное перемещение переводит систему OXY Z из положения 20 в положение 2; оставляя точки C и O и, следовательно, прямую OC неподвижными, что доказывает теорему.

изменения базисных векторов системы обусловлены только вращательным перемещением.

Ось, проходящая через т. O; относительно которой происходит поворот системы OX1X2X3; соответствующий изменениям d~ei векторов ~ei (i = 1; 2; 3) за бесконечно малый интервал времени dt; называется мгновенной осью вращения.

Единичный вектор вдоль оси вращения обозначим через ~ew . Направление этого вектора выбирается таким образом, чтобы с конца вектора ~ew вращение представлялось происходящим против часовой стрелки.

При вращательном движении за время dt все точки системы OX1X2X3 поворачиваются на угол d' в плоскостях, перпендикулярных мгновенной оси вращения.

В частности, единичные векторы ~ei получают приращения d~ei (i = 1; 2; 3); направленные перпендикулярно ~ew в сторону поворота системы и по величине равные

dei = id' = ei sin i d' = sin i d'; i = 1; 2; 3;

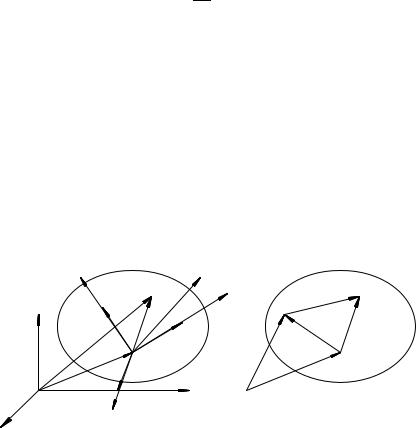
116 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА

ãäå i длина перпендикуляра, опущенного из конца вектора ~ei на ось вращения, i угол между векторами ~ew è ~ei(i = 1; 2; 3) (ñì.ðèñ. 65).

Поскольку d(~ei ~ei) = 0; òî d~ei ? ~ei; и, следовательно, вектор ~ew и приращения базисных векторов d~ei связаны соотношениями

Мгновенная угловая скорость !~ это вектор

направленный вдоль мгновенной оси вращения так, чтобы из его конца вращение системы OX1X2X3 выглядело против ча- совой стрелки, и длина которого равна модулю производной от угла поворота по времени.

5.2. Скорости точек тв¼рдого тела. Рассмотрим движение произвольной точки A твердого тела. Положение этой точки относительно системы координат OX1X2X3, жестко связанной с т.т., определяется радиус-вектором

Радиус-вектор ~r 0 задает положение т. A относительно ½неподвижной\ системы координат O0X10 X20 X30 (см. рис. 66). Обозна- чим через ~ro радиус-вектор центра O относительно системы координат O0X10 X20 X30 .

Очевидно, что ~r 0 = ~rO + ~r. Скорость т. A ~vA согласно определению и принятым обозначениям, будет

скорость центра O.

Преобразуем выражение (2.78). Для этого разделим левые и правые части соотношения (2.76) на интервал времени dt; за который произошли изменения d~ei базисных векторов ~ei(i =

Подставляя выражение (2.81) в формулу (2.78), окончательно находим

Как видно из равенства (2.82), скорость любой точки A твердого тела может быть выражена через скорость некоторой другой точки тела (полюса) O и угловую скорость !~. Первое слагаемое в формуле (2.82) определяет поступательную составляющую скорости, а второе вращательную составлящую.

Покажем, что угловая скорость !~ не зависит от выбора полюса. Для этого предположим противное: будем считать, что

118 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА

если за полюс выбрать точку O1, то угловая скорость равна !~1, а если полюсом является O2, òî !~2: Тогда по формуле (2.82) можно составить следующие соотношения:

Подставляем выражение для ~vO2 из третьей формулы во вторую и приравниваем правые части первой и второй формул:

Точка A выбрана произвольно, следовательно, последнее соотношение будет справедливо, если !~2 = !~1, что и требовалось доказать.

5.3. Ускорения тв¼рдого тела. Рассмотрим распределение ускорений в твердом теле. Для этого продифференцируем левую и правую части формулы (2.82) по времени. Учитывая равенство (2.81), получим

определяет поступательное ускорение, равное ускорению полюса O, а вектор

называется мгновенным угловым ускорением.

По величине и направлению ветор ~" совпадает со скоростью движения конца вектора угловой скорости !~.

есть вращательное ускорение. Этот вектор направлен перпендикулярно плоскости, проходящей через векторы ~" и ~r и по величине и направлению совпадает с тангенциальным (касательным) ускорением, которое имела бы та же самая точка при вращении с угловым ускорением " вокруг оси, совпадающей с направлением вектора ~". Эту ось называют осью ускорений.

При вращении вокруг неподвижной оси направления векторов !~ и ~" совпадают с одной осью, и в связи с этим в каждой точке векторы скорости и тангенциального ускорения направлены вдоль одной и той же прямой, касательной к траектории.

Вектор

называется осестремительным ускорением.

Обозначим ~e! единичный вектор мгновенной оси вращения. Тогда !~ = !~e! , и, раскрывая двойное векторное произведение (2.87), можно представить ~aoc â âèäå

~aoc = !~ (!~ ~r) = !~(!~ ~r) ~r(!~ !~) = = !2(~e! (~e! ~r) ~r):

Выясним геометрический смысл полученного выражения.

-~e! ~r проекция вектора ~r на направление мгновенной оси вращения;

-~e! (~e! ~r) вектор, направленный вдоль оси вращения, его длина равна проекции вектора ~r на ось вращения;

-~e! (~e! ~r) ~r вектор, направленный из рассматриваемой точки A к мгновенной оси вращения и перпендикулярный последней.

Следовательно, вектор ~aoc, отложенный из любой точки, направлен к мгновенной оси вращения.

Таким образом, ускорение ~a точки твердого тела в общем случае его движения складывается из трех составляющих: 1)

120 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА

поступательного ускорения ~aO , одинакового в данный момент для всех точек тела и равного ускорению полюса; 2) вращательного ускорения вокруг полюса ~aBP , равного по величине произведению углового ускорения на кратчайшее расстояние точки до оси вектора углового ускорения и направленного перпендикулярно к плоскости, проходящей через ось ~" и данную точку, в ту сторону, откуда вращение вектора углового ускорения к радиус-вектору точки по кратчайшему пути будет выглядеть происходящим против хода часовой стрелки; 3) осестремительного ускорения ~aoc, направленного перпендикулярно к мгновенной оси от точки в сторону этой оси и равного по величине произведению квадрата угловой скорости на кратчайшее расстояние точки до мгновенной оси вращения, проведенной через полюс.

5.4. Абсолютная скорость движения материальной точки. Для рассмотрения движение м.т. выберем систему от- сч¼та OX1X2X3, которая, в свою очередь, движется относительно ½неподвижной\ системы O0X10 X20 X30 . Движение т. A относительно ½неподвижной\ системы O0X10 X20 X30 называется абсолютным, относительно системы OX1X2X3 относитель-

ным, а движение системы OX1X2X3 относительно системы

O0X10 X20 X30 переносным.

Скорость т. A в абсолютном движении ~va, согласно опреде-

ãäå x1, x2, x3 координаты м.т. A в системе OX1X2X3. Скорость т. A в относительном движении ~vr (относительно

системы OX1X2X3), согласно определению, равна