
Беляев Ю.Н. Введение в векторный анализ
.pdf
Ÿ 3. Оси естественного тр¼хгранника |
|
|
|
|
|
|
|
101 |
||||||||||
Преобразуем данную формулу, используя равенства: (2.51) |
||||||||||||||||||
è (2.52) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
00 |
2 |
|
0 |
|
2 |
|
~r |
00 |
|
~r |
|
0 |
2 |
|
|
|
|
~r ~r |
|
|
|
|
|
|
|
|
||||||||
K2 = |
|
|
|
|
: |
(2.53) |
||||||||||||
|
|
3 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
Векторное тождество |
|
|
|
~r 0 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
~a |
2~ 2 |
|
|
~ |
|
2 |
|
|
|
~ |
|
2 |
|
|
|
|||
|
b |
(~a b ) |
|
= (~a b ) |
|
|
|
|
||||||||||
позволяет окончательно переписать кривизну кривой в виде
|
|
0 |
|
|
00 |
|
|
|
|
|
|
|
|
|
2 |
|
|
||
K2 = |
~r |
~r |
|
|
: |
(2.54) |
|||
|
|
|
|
|
|||||
|
|
|
2 |
3 |
|
|
|||
|
|
~r 0 |
|
|
|
|
|||
По формулам (2.53) или (2.54) можно вычислить кривизну линии в любой ее точке при произвольном параметрическом задании этой кривой.
П р и м е р 44. Кривизна траектории материальной точки, брошенной под углом к горизонту.
Уравнение траектории материальной точки, движущейся в однородном поле тяготения, порождающем ускорение свободного падения ~g, в векторном виде есть
|
~gt2 |
|
~r = ~r0 + ~v0t + |
|
; |
2 |
||
ãäå ~r0 è ~v0 соответственно радиус-вектор и скорость материальной точки в начальный момент времени. В данном случае скалярным параметром, определяющим вектор-функцию ~r, является время t.
Вычислим первую и вторую производные от ~r по t:
_ |
+ ~gt; |
• |
= ~g: |
~r = ~v0 |
~r |
Подставляем эти выражения в формулу (2.54)
K2 = |
(~v0 ~g)2 |
|
f(~v0 + ~gt)2g3 |
||
|
= |
|
v02g2 sin2 (~v0; ~g) |
: |
|
(v2 |
d |
|||
|
|
|||
|
; ~g) + g2t2)3 |
|
||
0 |
+ 2v0gt cos (~v0d |
|
||
102 Глава 2. |
ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА |
|||||||||
Предположим, что в начальный момент времени скорость |
||||||||||
материальной точки была направлена по горизонтали ((~v0; ~g) = |
||||||||||
90 ), тогда |
|
|
2 |
|
|
v2g2 |
|
|
|
d |
|
|
K |
= |
|
0 |
|
: |
|
|
|
|
|
|
(v2 |
+ g2t2)3 |
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
0 |
|
|
|
|
|
Очевидно, что кривизна траектории максимальна в начальный |
||||||||||
момент времени и минимальна в момент падения на землю. |
||||||||||
|
|
|
|
|
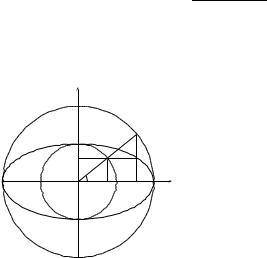
П р и м е р 45. Кривизна эллипса. |
|||||
y |
|
|
|
|
Выберем начало координат (рис. |
|||||
|
|
|
|
|
||||||
|
|
|
|
|
59) в центре эллипса, обозначим |
|||||
|
b |
|
|
|
буквами a и b большую и малую |
|||||
|
|
|
|
полуоси |
эллипса |
соответственно. |
||||
|
|
M |
|
|
||||||
|
|
|
|
Тогда координаты x и y произ- |
||||||
|
|
a x |
||||||||
|
" |
вольной точки M |
эллипса можно |
|||||||
|
|
|
|
|||||||
O |
|
|
|
|
||||||
|
|
|
|
задать параметрически: |
||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
x = a cos "; |
è |
y = b sin "; |
||
Ðèñ. 59 |
|
|
|
где угол " изменяется от нуля до |
||||||
|
|
|
2 . |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Следовательно, радиус-вектор т.M можно параметрически |
||||||||||
представить в виде |
|
|
|
|
|
|
|
|
|
|
~r = a cos " ~ex + b sin " ~ey :
Найдем первую и вторую производные радиус-вектора по " и выполним вычисления согласно формуле (2.54):
~r"0 = a sin " ~ex + b cos " ~ey ; ~r""00 = a cos " ~ex b sin " ~ey ;
|
|
|
|
|
~ex |
|
|
|
|
~ey |
|
~ez |
|
|
||||
|
|
|
|
|
|
|
a cos " |
|
|
b sin " 0 |
|
|
||||||
~r"0 |
|
~r""00 |
= |
|
|
a sin " |
|
b cos " |
|
0 |
|
= ab~ez ; |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
2 |
= a |
2 |
|
2 |
|
|
2 |
cos |
2 |
|
|
|
|
|
|
~r" |
|
|
sin " + b |
|
|
": |
|
||||||||

Ÿ 3. Оси естественного тр¼хгранника |
103 |
Поэтому
ab
K= a2sin2" + b2cos2" 3=2 :
3.4.Кручение пространственной кривой. Выразим кручение из второй формулы Френе: (2.42)
T |
= ~en dsb |
= ~en |
~e |
ds = ~e |
~en ds |
: |
||||||||||||
1 |
|
d~e |
|
|
|
|
|
d~en |
|
|
|
|
|
|
|
d~en |
|
|
Из первой формулы Френе (2.41) |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
d~e |
|
|
d2~r |
|
|
|
|
||||
|
|
|
|
~en = R |
|
= R |
|
|
|
; |
|
|
|
|
||||
|
|
|
ds |
ds2 |
|
|
|
|
||||||||||
следовательно, |
|
|
|
|
d3~r |
|
dR d2~r |
|
|
|
|
|||||||
|
|
|
|
d~en |
|
= R |
+ |
: |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
ds |
|
ds3 |
ds ds2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
Подставляем выражения (2.56) и (2.57) в формулу (2.55):
(2.55)
(2.56)
(2.57)
1 |
= |
d~r |
R |
d2~r |
|
R |
d3~r |
+ |
dR d2~r |
! |
= R2 |
d~r |
|
d2~r |
|
d3~r |
: (2.58) |
||
T |
ds |
ds2 |
ds3 |
ds |
|
ds2 |
ds |
ds2 |
ds3 |
||||||||||
Если кривая задана параметрическим уравнением с произвольным параметром ; нам нужно выразить в формуле (2.58) производные по s через производные по параметру .
В разделе 3.3. было найдено, что
0 |
0 |
1 |
|
00 |
00 |
1 |
|
|
0 s 00 |
(2.59) |
||||
~rs |
= ~r |
|
; |
~rss |
= ~r |
|
|
|
~r |
|
|
|
: |
|
0 |
0 |
|
2 |
0 |
3 |
|||||||||
|
|
s |
|
|
|
s |
|
|
|
s |
|
|
||
Очевидно, что третья производная от ~r по s будет содержать слагаемые, пропорциональные первой, второй и третьей производным от ~r по s:
000 |
000 |
1 |
00 |
0 |
|
(2.60) |
~rsss = ~r |
|
+ ~r f1 |
( ) + ~r |
f2( ); |
||
s 0 3 |
||||||
где явный вид функций f1( ) è f2( ) для нашей задачи не существенен. Подставляя выражения (2.59) и (2.60) в формулу
104 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
(2.58) и учитывая, что смешанное произведение трех векторов, два из которых одинаковы, равно нулю, получаем
|
T |
|
= R |
|
|
|
|
|
|
0 |
|
6 |
|
|
|
: |
||||
1 |
|
|
|
2 |
~r 0 |
|
|
~r 00 |
~r 000 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
||
Наконец, подставляя сюда выражение для R2 из формулы |
||||||||||||||||||||
(2.54), находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
~r |
0 |
|
|
~r |
00 |
|
~r 000 |
|
|
|
|||||||
|
|
= |
|
|
|
|
|
|
|
: |
(2.61) |
|||||||||
|
|
|
|
|
|
|
|
0 |
|
00 |
|
2 |
|
|||||||
|
|
T |
|
|
|
~r |
|
~r |
|
|
|
|
|
|||||||
Задачи
66.По заданным уравнениям движения точки найти: уравнение траектории, скорость и ускорение м.т.; тангенциальную
èнормальную составляющие ускорения, радиус кривизны траектории в момент времени t = 1 с:
1)~r = (3t 6)~ex + (2 2t)~ey ;
2)~r = 2t~ex + 8t2~ey ;
3)~r = (5 sin 8t)~ex + (5 cos 8t)~ey ;
4)~r = (2 3 cos 4t)~ex + (sin 4t 1)~ey ;
5)~r = (3t2)~ex + (5t2)~ey ;
6)~r = (4 cos 5t2)~ex + (4 sin 5t2)~ey ;
7)~r = (3t)~ex + (t3)~ey :
67.Определить кривизну и кручение винтовой линии
~r = A cos Bt ~ex + A sin Bt ~ey + Ct~ez :
Ÿ4. Криволинейные ортогональные системы координат
Âдекартовой системе координат положение точки M определяется тремя независимыми параметрами x, y; z, и заданные в трехмерном пространстве физические величины являются функциями этих трех координат.

Ÿ 4. Криволинейные ортогональные системы координат 105
Часто положение точки M в пространстве определяют с помощью криволинейных координат q1; q2; q3 тройки независимых величин, которые однозначно определяют положение точ- ки в пространстве и связаны с решаемой задачей более естественным образом, чем декартовые. Например, для задач с осевой симметрией в качестве криволинейных координат удобно использовать цилиндрические: q1 = расстояние от т. M до фиксированной прямой OZ; q2 = ' угол между фиксированной плоскостью OXZ и полуплоскостью, ограниченной осью OZ и проходящей через т. M ; q3 = z расстояние от точки M до плоскости, перпендикулярной оси OZ и проходящей через т. O (рис. 60), которое бер¼тся со знаком плюс в одном направлении от плоскости и минус в другом.
Z |
|
Z |
|
|
|
|
|
~ez |
|
|
~er |
|
~e' |
|
~e' |
|
M |
|
|
|
|
|
|
M |
~e |
|
~e |
z |
|
_ r |
|
O |
|
O |
|
^ |
Y |
^ |
Y |
' |
' |
||
X |
|
X |
|
Ðèñ. 60 |
|
Ðèñ. 61 |
|
Любая точка M трехмерного пространства может быть за- |
|||
дана в цилиндрической системе координат ; |
'; z, åñëè ïî- |
||
следние изменяются в пределах: 0 < 1; 0 ' < 2 ; 1 < z < 1: Связь между декартовыми и цилиндрическими координатами очевидна:
x = cos '; y = sin '; z = z: |
(2.62) |
Другой часто используемой системой координат является сферическая (см. рис. 61): q1 = r расстояние от фиксированной точки O до т. M ; q2 = угол между фиксированной осью OZ и радиус-вектором ~r т. M ; q3 = ' угол между фиксированной полуплоскостью OXZ и полуплоскостью, ограниченной осью OZ и проходящей через т. M . В этом случае
x = r sin cos '; y = r sin sin '; z = r cos ; |
(2.63) |
106 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
а пределами изменений сферических координат являются
0 r < 1; 0 ; 0 ' < 2 :
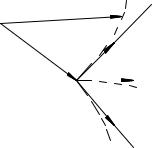
Пусть в некоторой криволинейной системе координат q1; q2; q3 точка M характеризуется координатами q1M ; q2M ; q3M : Координатной линией q1; проходящей через т.M , называется кривая, описываемая вектор-функцией (см. рис. 62)
~r = ~r(q1; q2M ; q3M );
где координаты q2 = q2M è q3 = q3M фиксированы, а координата q1 меняется в некотором интервале вблизи значения q1M . Касательная к этой линии в т. M называется координатной осью q1. Аналогично определяются координатные линии и оси q2 è q3.
|
|
|
Например, в цилиндричес- |
|
|
|
|
кой системе координат |
(ñì. |
~r(q1; q2M ; q3M ) |
|
рис. 60) координатной линией |
||
O |
|
îñü q1 |
q1 = является прямая, пер- |
|
|
|
|
||
~r(M ) |
~e1 |
|
пендикулярная оси OZ, коор- |
|
|
~e2 |
îñü q2 |
динатной линией q2 = ' |
|
|
окружность радиуса вокруг |
|||
M |
|
|
||
|
|
|||
|
|
оси OZ, координатной линией |
||
|
|
|
||
|
~e3 |
|
q3 = z прямая, перпенди- |
|
Ðèñ. 62 |
îñü q3 |
кулярная плоскости OXY . На |
||
|
|
|
рис. 60-62 координатные линии |
|
|
|
|
показаны штрихованными. |
|
Направления касательных к координатным линям qi |
(i = |
|||
1; 2; 3) (годографам ~r = ~r(qi)) совпадают с направлениями производных радиус-вектора ~r по соответствующей координате qi :
@~r |
= |
lim |
~r |
; i = 1; 2; 3: |
(2.64) |
|
|
||||
@qi |
qi!0 |
qi |
|
||
qj =0 j=6 i
Формулы (2.64) есть определения так называемых частных производных вектор-функции ~r = ~r(q1; q2; q3) по одной из переменных qi, когда две другие остаются постоянными. Чтобы

Ÿ 4. Криволинейные ортогональные системы координат 107
подчеркнуть, что речь идет о производной функции нескольких
переменных, используется обозначение |
@~r |
вместо d~r |
, принятого |
|
@qi |
||||
|
dq |
|
для производной вектор-функции одного переменного.
4.1. Базисные векторы и коэффициенты Ламе. Â
качестве единичных векторов, определяющих криволинейную систему координат в точке M , естественно принять
~ej = |
|
1 |
|
@~r |
; |
j = 1; 2; 3; |
(2.65) |
|
|
|
|
||||||
Hj @qj |
||||||||
где величины |
|
|
|
|
|
|
|
|
|
|
@~r |
|
|
|
|||
|
|
|
|
|
|
|
||
Hj = |
|
|
|
; |
j = 1; 2; 3 |
(2.66) |
||
@qj |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
называются единицами локальной длины, или коэффициентами Ламе3.
В декартовой системе координат радиус-вектор точки определяется координатами x; y; z :
~r = x~ex + y~ey + z~ez ;
ãäå îðòû ~ex; ~ey ; ~ez остаются постоянными для всех точек пространства. Поэтому, согласно правилам дифференцирования (2.4) и (2.5),
@~r |
= |
@x |
~ex + |
@y |
~ey + |
@z |
~ez ; |
|
|
|
|
||||
@qj |
@qj |
@qj |
@qj |
и коэффициенты Ламе (2.66) могут быть вычислены по формуле
Hj = v |
|
|
|
|
|
|
|
|
|
|
|
; j = 1; 2; 3: (2.67) |
|
@x |
2 |
+ |
@y |
2 |
+ |
@z |
2 |
||||
u |
|
|
! |
|
|
! |
|
|
|
! |
|
|
t |
|
|
|
|
|
|
|
|
|
|||
u |
|
@qj |
|
@qj |
|
|
@qj |
|
|
|||
Направления базисных векторов криволинейной системы координат, определяемых формулами (2.65), в общем случае меняются от точки к точке, и коэффициенты Ламе являются
3Gabriel Lame (1795-1870) французский математик, впервые вв¼л кри-
волинейные координаты в пространстве (1833)

108 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
функциями криволинейных координат Hj = Hj (qk ) (j; k = 1; 2; 3):
П р и м е р 46. Коэффициенты Ламе для сферической системы координат.
Используя соотношения (2.63) и обозначая H1 Hr, H2 H , H3 H', по формуле (2.67) находим
Hr
H
H'
= s |
|
sin cos ') |
2 |
@(r sin sin ') |
2 |
@(r cos ) |
2 |
|||
@(r |
+ |
+ |
= |
|||||||
|
|
|
|
|||||||
|
@r |
@r |
@r |
|||||||
q |
|
|
|
|
|
|
|
|
||
=sin2 cos2 ' + sin2 sin2 ' + cos2 = 1;
q
=r2 cos2 cos2 ' + r2 cos2 sin2 ' + r2 sin2 = r;
q
=r2 sin2 sin2 ' + r2 sin2 cos2 ' = r sin :
4.2. Скорость |
и ускорение |
материальной точки |
в криволинейной |
ортогональной |
системе координат. |
Радиус-вектор м.т. является функцией криволинейных координат, которые, в свою очередь, зависят от времени t:
~r = ~r(q1(t); q2(t); q3(t)):
По определению, скорость м.т. это производная радиусвектора по времени. Поэтому используя обозначения (2.65) и (2.66), ее можно записать в виде
|
|
3 |
|
|
|
3 |
|
|
d~r |
X |
@~r dqj |
X |
(2.68) |
||
~ = |
|
= |
|
|
|
= Hj qj~ej : |
|
|
dt |
j=1 |
@qj dt |
j=1 |
|
||
|
|
|
|
|
|
||
Координаты ускорения м.т. ~a в ортогональной системе координат равны проекциям вектора ~a на оси координат. Следовательно,
aj = ~a ~ej = |
d~ |
|
1 |
|
@~r |
= |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
dt |
Hj |
@qj |
|
@qj !# |
; |
(2.69) |
|||||||
= Hj |
" dt |
~ |
@qj |
! ~ dt |
|
||||||||
1 |
|
d |
|
|
@~r |
|
|
d |
|
@~r |
|
|
|

Ÿ 4. Криволинейные ортогональные системы координат 109
где j = 1; 2; 3: Преобразуем выражение (2.69). Для этого предварительно получим два вспомогательных равенства.
Ï å ð â î å ñ î î ò í î ø å í è å Ë à ã ð à í æ à4 . Дифференцируя выражение (2.68) по qj (j = 1; 2; 3); находим
|
|
|
|
|
|
|
|
|
|
|
|
@~ |
= |
|
@~r |
; |
|
j = 1; 2; 3: |
(2.70) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
@qj |
|
|
|
@qj |
|
|
|
|
|
|
|
||||||||||
|
В т о р о е с о о т н о ш е н и е Л а г р а н ж а. Возьмем производ- |
||||||||||||||||||||||||||||||||
ную по времени от |
|
@~r |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
dt @qj ! |
|
|
|
|
|
|
@qj |
+ @qj @q2 q2 |
+ @qj @q3 q3; j = 1; 2; 3: |
|||||||||||||||||||||||
|
= @qj @q1 q1 |
||||||||||||||||||||||||||||||||
|
d @~r |
|
|
|
@2~r |
|
|
|
|
@2~r |
|
|
@ |
2~r |
|
||||||||||||||||||
|
Вычислим производную по qj от обеих частей равенства |
||||||||||||||||||||||||||||||||
(2.68): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
@~ |
@2~r |
|
|
|
|
|
|
|
|
|
|
@2~r |
|
|
@2~r |
|
|
|
|||||||||||||
|
|
|
= |
|
|
|
q1 + |
|
|
|
|
|
|
q2 |
+ |
|
|
|
q3; j = 1; 2; 3: |
||||||||||||||
|
|
@qj |
@qj @q1 |
@qj @q2 |
@qj @q3 |
||||||||||||||||||||||||||||
|
Сравнивая последние два равенства, получаем второе соот- |
||||||||||||||||||||||||||||||||
ношение Лагранжа: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
d |
|
|
|
@~r |
! |
|
= |
|
@~ |
; |
|
j = 1; 2; 3: |
(2.71) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
dt |
|
|
|
@qj |
|
@qj |
|
||||||||||||||||||
|
Применим соотношения Лагранжа (2.70) и (2.71) к форму- |
||||||||||||||||||||||||||||||||
лам (2.69). Результатом является |
|
|
|
|
|
||||||||||||||||||||||||||||
|
aj = Hj |
" dt |
~ @qj ! ~ |
@qj # = |
|
|
|
||||||||||||||||||||||||||
|
1 |
|
d |
|
|
|
|
|
|
@~ |
|
|
|
|
|
|
@~ |
|
|
|
|
|
|||||||||||
|
|
= Hj |
" dt |
@qj |
2 |
|
!! |
@qj |
2 |
!# ; |
j = 1; 2; 3:(2.72) |
||||||||||||||||||||||
1 |
|
d |
@ |
|
|
|
|
|
|
2 |
|
|
|
|
|
@ |
|
2 |
|
|
|
||||||||||||
Для вычисления ускорения по формулам (2.72) необходимо предварительно с помощью формулы (2.68) найти квадрат скорости 2 = ~ ~ :
4Joseph Louis Lagrange (1736-1813).
110 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
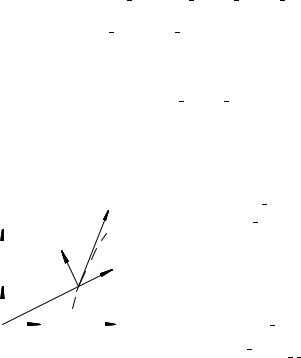
П р и м е р 47. Компоненты скорости и ускорения в полярной системе координат q1 = r; q2 = ' (ðèñ. 63).
Отметим, что полярную систему координат можно использовать при плоском движении материальной точки.
Предварительно найдем коэффициенты Ламе. По формуле (2.67) можно найти: H1 Hr = 1 è H2 H' = r. Подстановка этих значений коэффициентов Ламе в формулу (2.68) дает
~v = H1q1~e1 + H2q2~e2 = r~er + r'~e'; |
(2.73) |
где величины vr = r è v' = r' называются радиальной и транс-
версальной составляющими скорости соответственно. Для квадрата модуля скорости имеем
v2 = r2 + r2'2:
Компоненты ускорения вычисляем по формулам (2.72):радиальная составляющая ускорения
|
|
|
|
|
ar = |
d @(v2 =2) |
|
@(v2=2) |
= |
||||||||||||
|
|
|
|
|
dt |
|
|
|
@r |
|
@r |
||||||||||
|
|
|
~ |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
(2.74) |
|||
|
|
|
= r• r' ; |
|
|
|
|
||||||||||||||
Y |
|
|
|
|
|
|
|
|
|||||||||||||
|
~e' |
|
|
трансверсальная составляющая ус- |
|||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
корения |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
~er |
|
|
|
|
|
|
|
|
||||||||||
~ey |
)' |
a' = r |
|
" dt @' |
|
@(@' |
# = |
||||||||||||||
|
|
r |
|
|
|
1 d @(v2=2) |
|
|
v2 =2) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
~ex |
|
X |
|
1 d(r2 |
') |
|
|
|
|
|
|
|
||||||||
|
|
= |
= 2r' + r':• |
(2.75) |
|||||||||||||||||
|
Ðèñ. 63 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
r |
|
|
|
dt |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
П р и м е р 48. Найти уравнение траектории м.т. и ее ускорение при плоском движении, если радиальная vr и трансверсальная v' составляющие ее скорости задаются соотношениями
1 |
|
è |
1 |
|
||
vr = |
|
; |
v' = |
|
; |
|
r2 |
cr |
|||||
где c постоянная.
