
Беляев Ю.Н. Введение в векторный анализ
.pdfŸ 2. Векторное поле |
151 |
Задание векторных линий да¼т только направление вектора во всякой точке поля. Величину вектора можно характеризовать густотой проводимых линий числом линий, проходящих через единичную площадку, перпендикулярную линиям поля в рассматриваемой точке.
Векторное поле скоростей точек твердого тела графически может быть представлено (см. П р и м е р 66) как система концентрических окружностей, причем ½интенсивность кручения\скорость отдельной точки, определяется вектором угловой скорости !~, одинаковым для всех точек твердого тела.
Более сложный характер может иметь вращательное движение элемента объема жидкой или газообразной среды. Степень закрученности движения малых элементов таких сред в общем случае различна и описывается вектор-функцией, получившей название вихрь или ротор векторного поля. Прежде чем дать определение этого вектора, напомним, что есть
2.2.Криволинейный интеграл от векторного поля.
~
Возьмем в области , в которой определено векторное поле P , некоторую кривую L. Разобъем кривую L с помощью точек M1(~r1), M2(~r2), : : :, Mn(~rn) на малые дуги, которым соответствуют элементарные перемещения ~ri = ~ri+1 ~ri.
Составим сумму
Xn ~ ~
P (ri ) ~ri;
i=1
~ ~
ãäå P (ri ) значение векторного поля в какой-нибудь точке
~
Mi (ri ), принадлежащей дуге MiMi+1.
Если при неограниченном возрастании числа элементов ~ri и убывании до нуля длины j ~rij наибольшего из элементов ~ri имеется конечный предел
|
|
i |
n |
|
|
|
|
|
|
|
|
X |
~ ~ |
|
|
|
|
||
|
|
lim |
|
P (r |
i |
) |
|
~r |
; |
|
|
n!1 |
|
|
|
i |
|
||
|
|
max j ~r j!0 i=1 |
|
|
|
|
|
|
|
не зависящий ни от способа разбиения кривой L, ни от выбора |
|||||||||
|
~ |
) на дугах MiMi+1, то он называется криволиней- |
|||||||
точек Mi |
(ri |
||||||||
152 |
|
|
|
|
Глава 3. |
|
ФУНКЦИИ ТОЧКИ |
|
|
|
|
|
|
~ |
|
|
|
ным интегралом векторного поля P вдоль кривой L и обозна- |
||||||||
чается |
|
|
|
|
|
|
|
|
n |
|
|
|
|
L |
|
|
|
X |
~ ~ |
|
|
|
|
|
||
lim |
P (r |
i |
) |
|
~ri = P |
|
d~r: |
(3.22) |
n!1 |
|
|
|
Z |
|
|
|
|
max j ~rij!0 i=1 |
|
|
|
|
|
|||
Отметим два свойства криволинейного интеграла от векторного поля, которые очевидным образом следуют из его определения.
1. Если под знаком интеграла имеется постоянный множитель, его можно вынести за знак интеграла:
Z |
P~ d~r = Z |
P~ d~r; = const: |
(3.23) |
L |
L |
|
|
2. Интеграл по составной кривой ABC равен сумме интегралов по отдельным ее участам AB и BC:
Z |
P~ d~r = Z |
P~ d~r + Z |
P~ d~r: |
(3.24) |
AC |
AB |
BC |
|
|
3. При изменении направления интегрирования по кривой L интеграл меняет свой знак:
Z |
Z |
|
|
~ |
|
~ |
(3.25) |
P d~r = P d~r: |
|||
L |
L |
|
|
|
|
||
Замечая, что jd~rj = ds, где ds элемент длины кривой, можно записать интеграл (3.22) в виде
ZZ
~
P d~r = Psds;
LL
~
ãäå Ps касательная составляющая векторного поля P к кривой L.
Другая форма представления криволинейного интеграла основана на выражении скалярного произведения в декартовой системе координат
~
P d~r = Pxdx + Py dy + Pz dz;
Ÿ 2. Векторное поле |
153 |
поэтому
ZZ
~
P d~r = Pxdx + Py dy + Pz dz :
LL
2.3. Вычисление криволинейного интеграла может быть сведено к нахождению определенного интеграла.
Преобразуем скалярное произведение в левой части формулы (3.22). В декартовой системе координат
~ri = ~ri+1 ~ri = (xi+1 xi)~ex + (yi+1 yi)~ey + (zi+1 zi)~ez= = xi ~ex + yi ~ey + zi ~ez ;
~ ~ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
P (ri ) = Px(xi |
; yi |
; zi )~ex + Py (xi ; yi ; zi )~ey |
+ Pz (xi ; yi |
; zi )~ez : |
||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
n |
|
|
|
|
|
|
i |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
X |
~ |
~ |
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
||||
lim |
|
P (r |
i |
) |
~r |
= |
lim |
|
P |
(x |
; y |
; z |
|
) x |
i |
+ |
|
|||||
n!1 |
|
|
|
|
i |
|
n!1 |
x |
|
i |
i |
i |
|
|
|
|
|
|
|
|||
max r !0 i=1 |
|
|
|
|
|
max j x j!0 i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
i |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
(x ; y ; z ) y |
|
|
|
||||||||
|
|
|
|
|
|
|
+ |
lim |
P |
i |
+ |
|||||||||||
|
|
|
|
|
|
|
|
n!1 |
|
y |
|
i |
i |
|
i |
|
|
|
|
|||
|
|
|
|
|
|
|
|
max j y j!0 i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
i |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
(x ; y ; z ) z |
|
: (3.26) |
|||||||||
|
|
|
|
|
|
|
+ |
lim |
P |
|
||||||||||||
|
|
|
|
|
|
|
|
n!1 |
|
z |
|
i |
i |
|
i |
|
|
i |
|
|
||
max j z j!0 i=1
Пусть кривая L задана уравнениями в параметрической форме x = X(t), y = Y (t), z = Z(t). Следовательно,
xi = X(ti+1) X(ti); |
(3.27) |
yi = Y (ti+1) Y (ti); |
|
zi = Z(ti+1) Z(ti): |
|
Преобразуем первое из равенств системы (3.27) по формуле Лагранжа
|
dX |
|
|
0 |
|
|
|
|
|
|
|
xi = |
dt |
t= i |
(ti+1 |
ti) = Xt ( i) ti; |
(3.28) |
|
|
|
|
|
|
ãäå i 2 [ti; ti+1] :
154 Глава 3. ФУНКЦИИ ТОЧКИ
Точка M , согласно определению (3.22), может быть взята произвольно на дуге MiMi+1. Выберем ее так, чтобы координаты точки M на каждом из участков разбиения кривой L соответствовали значению параметра t = i. Тогда с учетом равенства (3.28)
Px(xi ; yi ; zi ) xi = Px [X( i); Y ( i); Z( i)] Xt0 ( i) ti
и первая предельная сумма равенства (3.26) перепишется в виде
n |
|
|
|
|
|
|
|
X |
0 |
|
|
lim |
Px(x ; y ; z ) xi = Px [X(t); Y (t); Z(t)] X |
(t)dt; |
|
n!1 |
i i i |
|
|
max j xij!0 i=1 |
Z |
|
|
где t = и t = соответствуют координатам начала и конца кривой интегрирования L.
Преобразуем аналогичным образом две другие предельные суммы в (3.26). В итоге получаем
Z Z n
~ 0
P d~r = Px [X(t); Y (t); Z(t)] X (t) +
+ Py [X(t); Y (t); Z(t)] Y 0(t) + o
+ Pz [X(t); Y (t); Z(t)] Z 0(t) dt: (3.29)
Необходимыми и достаточными условиями существования
~
криволинейного интеграла векторного поля P вдоль кривой L являются следующие:
1)функции Px, Py , Pz должны быть непрерывны вдоль кривой L;
2)функции X(t); Y (t); Z(t) должны иметь непрерывные
производные по аргументу t.
~ |
3 |
2 |
~ey |
П р и м е р 68. Вычислить работу силы F |
= x |
~ex + 3zy |
x2y~ez при движении м.т. вдоль отрезка прямой, идущей от т.
M (3; 2; 1) äî ò. N (0; 0; 0).
|
Решение. Уравнение прямой проходящей через точки M и |
|||||||
N : |
|
x |
|
y |
|
z |
|
|
|
|
= |
= |
: |
||||
|
|
3 |
|
|
|
|||
|
|
2 |
1 |
|
||||
Ÿ 2. Векторное поле |
155 |
Приравняем каждое из отношений последней формулы параметру t, в результате получим уравнение прямой в параметри- ческой форме:
|
|
x = 3t; |
y = 2t; |
|
z = t: |
|
|
||||||
Соответственно, dx = 3dt; dy = 2dt; dz = dt, и |
|
|
|||||||||||
~ |
3 |
+ 6zy |
2 |
2 |
|
3 |
3 |
3 |
3 |
: |
|||
F d~r = (3x |
|
|
x |
y)dt = (81t |
+ 24t |
18t |
)dt = 87t |
||||||
Точке M соответствует t = 1, а N t = 0. По формуле |
|||||||||||||
(3.29) находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
0 |
87t3dt = 4 : |
|
|
|
|||
|
|
F~ d~r = Z |
|
|
|
||||||||
|
|
|
|
|
|
|
|
87 |
|
|
|
|
|
|
|
M N |
|
|
|
1 |
|
|
|
|
|
|
|
Особый интерес представляет случай, когда кривая интегрирования L замкнута и криволинейный интеграл берется по всей кривой. Такой интеграл называется циркуляцией C век-
~
торного поля P (M ) вдоль кривой L и обозначается
I |
|
~ |
(3.30) |
C = P d~r: |
L
За положительное направление обхода плоского контура L принято считать такой, при котором область , охватываемая контуром L, оста¼тся слева.
~
П р и м е р 69. Вычислим циркуляцию векторного поля P =y~ex + x~ey по контуру круга x2 + y2 = R2.
Координаты точек окружности выразим функциями одного параметра ' угла между радиусом окружности и осью X. Имеем
x = R cos '; |
y = R sin ' |
è |
|
dx = R sin ' d'; |
y = R cos ' d': |
Для вычисления циркуляции выполняем интегрирование по параметру ' в пределах от 0 до 2 .
IZ2
~ |
2 |
: |
P d~r = |
R cos ' R cos ' d' + R sin ' R sin 'd' = 2 R |
|
L |
0 |
|

156 |
Глава 3. ФУНКЦИИ ТОЧКИ |
2.4.Вихрь векторного поля. Пусть в области опре-
~
делено непрерывное векторное поле P . Возьмем в некоторой точке M 2 любое направление ~en и окружим точку M замкнутой кривой `, лежащей в плоскости, перпендикулярной направлению ~en. Обозначим площадь площадки, охватываемой контуром `.
Выберем направление единичного вектора ~en к площади таким образом, чтобы из конца вектора ~en положительное движение по контуру ` выглядело происходящим против хода ча- совой стрелки (правило правого винта).
|
|
~ |
В и х р е м в е к т о р н о г о п о л я P (M ) в т. M называет- |
||
ся вектор, обозначаемый символом |
2 |
~ |
|
rot P , проекция которого |
|
на направление ~en равна пределу отношения циркуляции век-
торного поля ~ по контуру , ограничивающему плоскую
P (M ) `
площадку , перпендикулярную в т. M этому направлению ~en, к площади , когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку M :
|
|
|
~ |
|
|
|
|
~ |
lim |
` P d~r |
= |
dCn |
|
(3.31) |
|
H |
|
|
: |
||||
rot nP = |
!0 |
|
|
d n |
|
||
|
|
|
|
|
|
||
Обозначения, используемые в правой части определения (3.31), имеют следующий смысл: dCn элементарная циркуляция вдоль границы элементарной площадки d n, перпендикулярной направлению ~en.
В и х р ь в о р т о г о н а л ь н о й с и с т е м е к о о р д и н а т. Всякий вектор полностью определяется своими координатами. Поэтому для нахождения вихря векторного поля в некоторой
~
точке M достаточно определить три проекции rot P на взаимно ортогональные оси системы координат.
Элементарное перемещение d~r в криволинейной ортогональной системе координат
d~r = ~e1d`1 + ~e2d`2 + ~e3d`3
выражается через элементарные перемещения d`1, d`2, d`3 вдоль первой, второй и третьей координатных линий соответ-
2От английского слова rotation вращение.
Ÿ 2. Векторное поле |
157 |
ственно. Перемещения d`1, d`2, d`3, в свою очередь, выражаются с помощью коэффициентов Ламе через дифференциалы dq1; dq2; dq3:
d`1 = H1dq1; d`2 = H2dq2; d`3 = H3dq3;
~
так что скалярное произведение поля P на перемещение d~r равно
~
P d~r = P1H1dq1 + P2H2dq2 + P3H3dq3:
~
Для вычисления проекции rot P на первую координатную ось q1, проходящую через точку M , найдем циркуляцию поля
~
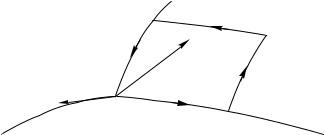
P по контуру M N KLM (см. рис. 85), охватывающему малую часть координатной поверхности q1 = const = q1M , перпендикулярную в каждой своей точке
q3
L
|
|
K |
|
|
~ |
|
|
P |
|
~e1 |
|
q1 |
M |
q2 |
|
||
|
|
N |
Ðèñ. 85
первой координатной оси. Если в замкнутом контуре M N KLM координаты точки M есть q1; q2; q3, то три другие узловые точки имеют следующие координаты:
N (q1; q2 + q2; q3); K(q1; q2 + q2; q3 + q3); L(q1; q2; q3 + q3):
Первая координата у всех точек рассматриваемого контура одинакова, поэтому мы не будем ее указывать при записи функций, которые потребуются для нахождения проекции вихря на первую ось.
Искомая циркуляция
I I
~
C1 = P d~r = P2H2dq2 + P3H3dq3 =
M N KLM |
M N KLM |
158 |
Глава 3. ФУНКЦИИ ТОЧКИ |
|
Z |
Z |
(3.32) |
= P2H2dq2 + P2H2dq2 + |
||
M N |
KL |
|
Z |
Z |
(3.33) |
+ |
P3H3dq3 + P3H3dq3: |
|
N K |
LM |
|
Рассмотрим первый из интегралов (3.32). По теореме о сред- |
||
íåì |
|
|
Z |
|
(3.34) |
P2H2dq2 = P2H2(q2; q3) q2; |
||
M N
где выражение P2H2(q2; q3) означает, что произведение двух функций P2 è H2 взято в некоторой точке дуги M N .
Аналогично для второго из интегралов (3.32)
Z
P2H2dq2 = P2H2(q2; q3 + q3) q2; |
(3.35) |
KL
аргумент (q2; q3 + q3) функции P2H2 соответствует некоторой точке дуги KL. При движении от т. K к т. L по дуге KL координата q2 уменьшается, поэтому правая часть формулы (3.35), в отличие от (3.34), содержит знак минус.
Два интеграла (3.32) в сумме дают
Z |
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P2H2dq2 + |
|
|
P2H2dq2 = |
|
|
|
|
|
|
|
|
|
|
||||
M N |
KL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
|
(P |
H |
(q ; q |
3 |
+ q |
) |
|
P |
H |
(q ; q |
)) q |
2 |
= |
|||
|
2 |
2 |
2 |
|
3 |
|
2 |
2 |
2 3 |
|
|
||||||
= |
|
|
@(P2H2) |
q |
q |
; |
|
|
|
|
|
|
|
(3.36) |
|||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
@q3 |
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
||
причем приближенное равенство (3.36) выполняется тем точ- нее, чем меньше размеры контура M N KLM .
Точно так же два интеграла (3.33) можно представить в виде
Z |
P |
H |
dq |
|
+ |
Z |
P |
H |
dq |
= |
@(P3 H3) |
q |
q |
: |
(3.37) |
|
@q2 |
||||||||||||||
3 |
3 |
|
3 |
|
3 |
3 |
|
3 |
2 |
3 |
|
|
N K |
LM |
Ÿ 2. Векторное поле |
|
|
|
|
159 |
|
Складывая формулы (3.36) и (3.37) и стягивая |
контур |
|||||
M N KLM в точку M , находим элементарную циркуляцию: |
||||||
dC1 = |
@(P3H3) @(P2 H2) |
dq2dq3: |
(3.38) |
|||
|
|
|
|
|||
@q2 |
@q3 |
|||||
Разделив элементарную циркуляцию dC1 на соответствующую ей элементарную площадь
d 1 = d`1d`2 = H1H2dq1dq2;
найдем проекцию вихря на первую координатную ось:
rot 1P~ |
= |
1 |
|
@(P3H3) |
|
@(P2 H2) |
: |
(3.39) |
|
H2H3 |
@q2 |
@q3 |
|
||||||
Аналогичным образом находятся две другие проекции вихря. Формулы для второй и третьей проекций отличается от (3.39) циклической перестановкой индексов: 1 ! 2 ! 3 ! 1. В результате получается следующая формула для вихря:
rot P~ |
= |
1 |
|
@(P3H3) |
|
@(P2H2) |
~e1 + |
|
|
|||||||||
H2H3 |
@q2 |
|
|
@q3 |
|
|
|
|||||||||||
|
|
+ H3H1 |
@q3 |
|
|
@q1 |
|
~e2 + |
|
|||||||||
|
|
|
|
1 |
|
|
@(P1 H1) |
|
@(P3H3) |
|
|
|
|
|||||
|
|
|
|
+ |
|
1 |
|
|
@(P2H2) |
|
@(P1 H1) |
~e3 |
: (3.40) |
|||||
|
|
|
|
H1H2 |
|
@q1 |
|
@q2 |
|
|||||||||
Чтобы применить эту формулу к конкретной криволинейной ортогональной системе координат, нужно подставить в (3.40) соответствующие коэффициенты Ламе.
П р и м е р 70. В и х р ь в д е к а р т о в о й с и с т е м е к о о р- д и н а т. Коэффициенты Ламе: Hx = 1; Hy = 1; Hz = 1:
rot P~ = |
@P |
@P |
~ex + |
@P |
@P |
~ey + |
@P |
@P |
~ez : (3.41) |
|||
z |
|
y |
x |
|
z |
y |
|
x |
||||
@y |
@z |
@z |
@x |
@x |
@y |
|||||||
Эту формулу легко запомнить, если воспользоваться следующей символической записью:
|
|
~ex |
~ey |
~ez |
|
|
|
||||||
|
|
Px |
Py |
Pz |
|
|
|
||||||
|
|
@ |
|
@ |
|
@ |
|
|
|
|
|||
rot P~ = |
|
|
@x |
|
@y |
|
@z |
|
; |
(3.42) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

160 |
Глава 3. ФУНКЦИИ ТОЧКИ |
которая для получения результата (3.41) должна раскрываться по формуле определителя матрицы 3 3.
П р и м е р 71. Найти вихрь напряж¼нности гравитационного поля Земли.
Напряж¼нность поля тяготения Земли в некоторой точке M (~r) это сила, действующая со стороны Земли на материальную точку единичной массы, помещ¼нную в эту точку
~ |
|
m |
|
F |
= |
r3 |
~r ; |
где m масса Земли, гравитационная постоянная, ~r радиус-вектор, провед¼нный из центра Земли в точку M .
В декартовой системе координат r = px2 + y2 + z2. Воспользуемся формулой (3.41). Вычисляем производные:
@yz |
= m @y |
(x2 |
+ y2z+ z2)3=2 |
= m3zy(x2 + y2 + z2) 5=2; |
|||
@F |
|
@ |
|
|
|
|
|
@zy |
= m @z |
(x2 |
+ y2y+ z2)3=2 |
= m3yz(x2 + y2 + z2) 5=2: |
|||
@F |
@ |
|
|
|
|
|
|
~
Следовательно, rot xF = 0. Точно так же доказывается равенство нулю двух других координат ротора. Таким образом,
rot r3 ~r |
= ~0: |
||
|
|
m |
|
2.5. Смысл вектора |
~ |
Рассмотрим абсолютно |
|
rot P . |
|||
тв¼рдое тело, вращающееся с угловой скоростью !~ вокруг неподвижной оси. Поле скоростей такого тела выражается формулой
~v = !~ ~r;
где ~r радиус-вектор точки тела. По формуле (3.41) находим
rot ~v = 2!:~
Более сложный характер имеет поле скоростей движущейся жидкости. Движение малого элемента жидкости складывается
