
Беляев Ю.Н. Введение в векторный анализ
.pdf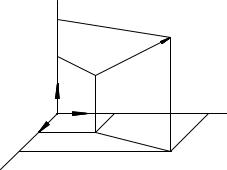
Ÿ 7. Вектор в ортонормированном базисе |
51 |
использовать тройку единичных взаимно ортогональных векторов ~e1, ~e2, ~e3 (такой базис называется ортонормированным), направленных вдоль осей Ox1; Ox2; Ox3 (рис.36), то координатами вектора ~a будут проекции этого вектора на выбранные оси. Покажем это с помощью следующих построений.
Через начало A и конец B вектора ~a проведем плоскости, перпендикулярные осям координат x1; x2; x3. Точки пересече- ния этих плоскостей с осями координат обозначим A1, A2, A3 è B1, B2, B3. На рис. 36 показаны также принадлежащие этим плоскостям отрезки: A12A1 è B12B1, перпендикулярные оси x1; A12A2 è B12B2, перпендикулярные оси x2; AA3, BB3, перпендикулярные оси x3; AA12 è BB12, перпендикулярные плоскости
Ox1x2.
|
|
|
|
|
|
|
Из построения оче- |
|||
B3 |
x3 |
|
|
|
|
видны равенства: |
||||
|
|
B |
|
|
|
|
|
|
||
|
|
|
|
|
|
OB3 |
= |
B12B; |
||
A3 |
|
~a |
|
|
|
|||||
|
|
|
|
OA3 |
= |
A12A; |
||||
A |
|
|
|
|||||||
|
|
|
|
|
||||||
~e3 |
~e2 |
A2 |
|
B2 |
и, следовательно, |
|||||
|
|
|
||||||||
~e1 |
|
|
|
|
|
|
||||
O |
|
|
|
x2 |
AA12 + B12B = A3B3: |
|||||
A1 |
|
A12 |
|
|
|
! |
! |
! |
||
B1 |
|
B12 |
|
|
|
|
|
|
||
|
|
|
|
|
Разлагая ~a на составля- |
|||||
x1 |
|
|
|
|
|
|||||
|
Ðèñ. 36 |
|
|
|
ющие, имеем |
|
|
|||
|
|
|
|
|
|
|
||||
~a = AA12 |
+ A12B12 |
+ B12B = A12B12 + A3B3 |
= |
|
||||||
|
|
! ! ! ! ! |
(1.74) |
|||||||
|
= A1B1 |
+ A2B2 + A3B3 |
|
= a1~e1 + a2~e2 + a3~e3; |
||||||
|
|
! |
! |
! |
|
|
|
|
|
|
ãäå ai = AiBi; i = 1; 2; 3; по определению разложения вектора в |
||||||||||
единичном базисе есть координаты вектора ~a в базисе ~e1, ~e2, ~e3, |
||||||||||
а по построению величины ai являются проекциями вектора ~a |
||||||||||
íà îñè Ox1; Ox2; Ox3; соответственно, согласно (1.56), равны |
||||||||||
~a; ~e |
); i = 1; 2; 3: |
(1.75) |
ai = a cos ( di |
|
|
52 |
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
|||
7.2. |
Длина вектора ~a в ортонормированном базисе, со- |
|||
гласно теореме Пифагора, вычисляется по формуле |
|
|||
|
a = q |
|
; |
|
|
a12 + a22 + a32 |
(1.76) |
||
ãäå ai; i = 1; 2; 3; проекции вектора на оси координат (см. рис. 36).
7.3. Направляющие косинусы. Направление вектора
~a относительно координатных осей Ox1; Ox2; Ox3 определяют с помощью направляющих косинусов вектора ~a
cos (~a; ~ei) = |
|
ai |
; i = 1; 2; 3: |
(1.77) |
d |
q |
|
|
|
(a21 + a22 + a23)
Сумма квадратов направляющих косинусов любого вектора ~a равна единице:
cos |
2 |
~a; ~e |
) + cos2 (~a; ~e |
) + cos2 (~a; ~e |
) = 1: |
(1.78) |
|
( d1 |
d2 |
d3 |
|
|
В этом легко убедиться, если возвести три равенства (1.77) в квадрат, сложить их и использовать формулу (1.76).
7.4. Угол между направлениями. Зная координаты вектора ~a в ортонормированном базисе, можно вычислить его проекцию на любое направление `. Для нахождения последней спроецируем обе части равенства (1.74) на ось `:
d |
d |
d |
(1.79) |
a` = a1 cos(~e`; ~e1) + a2 cos(~e`; ~e2) + a3 cos(~e`; ~e3 ): |
|||
Заменим левую часть равенства (1.79), используя выражение (1.56) для проекции вектора на ось, а координаты a1; a2; a3 представим согласно формуле (1.75). После этого разделим полученное соотношение на a. В результате получим
d` |
d |
d |
d |
d |
cos(~a; ~e |
) = cos(~a; ~e1) cos(~e`; ~e1) + cos(~a; ~e2) cos(~e`; ~e2) + |
|||
dd
+cos(~a; ~e3) cos(~e`; ~e3):

Ÿ 7. |
Вектор в ортонормированном базисе |
|
53 |
||||
|
7.5. |
Радиус-вектор |
точки M в декартовой системе ко- |
||||
ординат Oxyz (рис. 37) равен |
|
|
|
||||
~rM = xM ~ex + yM ~ey + zM ~ez ; |
|
|
z |
|
|||
|
|
|
|
|
zM |
|
|
где координаты xM ; yM ; zM |
|
|
|||||
|
|
|
|||||
вектора ~rM однозначно харак- |
|
|
M |
||||
теризуют точку M . Поэтому |
|
|
|||||
|
~r |
|
|||||
xM ; yM ; zM называют |
коорди- |
|
|
||||
~ez |
M |
|
|||||
|
|
||||||
натами |
точки M и пишут |
|
yM |
||||
|
~ey |
||||||
M (xM ; yM ; zM ). |
|
|
O |
||||
|
|
|
y |
||||
|
Соответственно, равенство |
~ex |
|
||||
|
x |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
~r = x~ex + y~ey + z~ez |
(1.80) |
x |
Ðèñ. 37 |
|
|||
выражает радиус-вектор ~r произвольной точки с координатами |
|||||||
x; y; z. |
|
|
|
|
|
|
|
|
Длина радиус-вектора ~r точки в декартовой системе коор- |
||||||
динат есть |
r = qx2 + y2 + z2: |
|
|
||||
|
|
|
|
|
|||
Ï ð è ì å ð 19. Ó ð à â í å í è ÿ ï ð ÿ ì î é |
â ä å ê à ð ò î â î é |
|||
ñ è ñ ò å ì å |
к о о р д и н а т. Воспользуемся |
уравнением |
(1.10), |
|
определяющим уравнение |
прямой, проходящей через |
точку |
||
|
~ |
~ |
|
обозна- |
A(~a) параллельно b: ~r = ~a + b. Координаты точки A |
||||
чим через |
|
|
~ |
|
x1, y1, z1, а координаты вектора b через `; m; n. |
||||
Согласно свойствам (1.47) и (1.49), векторное равенство (1.10) эквивалентно трем скалярным, которые называются параметрическими уравнениями прямой:
x = x1 + ` ; |
|
y = y1 + m ; |
(1.81) |
z = z1 + n :
Если считать параметр за время, то уравнения (1.81) опре-
деляют закон движения м.т. из точки A(x1; y1; z1) по прямой с p
постоянной скоростью v = `2 + m2 + n2 .

54 |
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
||||||
|
Если координаты `; m; n не равны нулю, равенства (1.81) |
||||||
можно записать в форме |
|
|
|
|
|
|
|
|
x x1 |
= |
y y1 |
= |
z z1 |
; |
(1.82) |
|
` |
|
m |
|
n |
|
|
они являются каноническими уравнениями прямой. |
|||||||
|
|
|
|
~ |
равна нулю, то со- |
||
|
Если какая-либо из координат вектора b |
||||||
ответствующая координата прямой не изменяется (прямая перпендикулярна соответствующей оси координат). Например, при
` = 0 будет x = x1 = const.
Для нахождения координатной формы уравнения прямой, проходящей через две различные точки, можно воспользоваться формулой (1.11): ~r = ~r1 + ~r2 при условии + = 1. Обозначим декартовые координаты точек M1(~r1) è M2(~r2) ÷å- ðåç (x1; y1; z1) è (x2; y2; z2) соответственно. Векторное равенство (1.11) эквивалентно трем скалярным:
x = (1 |
)x1 + x2; |
(1.83) |
y = (1 )y1 + y2; |
(1.84) |
|
z = (1 )z1 + z2; |
(1.85) |
|
где x; y; z координаты |
произвольной точки |
прямой M с |
радиус-вектором ~r. |
|
|
Параметр во всех трех равенствах (1.83-1.85) один и тот же; выражая из этих трех равенств и приравнивая, получим
уравнение прямой, проходящей через две точки M1 è M2:
x x1 |
= |
y y1 |
= |
z z1 |
: |
(1.86) |
x2 x1 |
|
y2 y1 |
|
z2 z1 |
|
|
Уравнения прямой на плоскости, в формах, аналогичныx (1.81), (1.82), (1.86), получаются очевидным образом. Для этого достаточно положить одну из координат для всех точек равной нулю, например z = z1 = z2 = 0.
П р и м е р 20. Найд¼м уравнение прямой линии, проходя-
щая через точки A(1; 2) и B( 4; 6): |
|
|
||||||||||
Из уравнений (1.83) и (1.84) |
получаем |
|||||||||||
|
x 1 |
= |
y |
2 |
; èëè |
y = |
|
0:8x + 2:8: |
||||
|
|
4 |
|
1 |
6 |
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
Ÿ 7. Вектор в ортонормированном базисе |
55 |
7.6.Определение векторной суммы методом проек-
|
|
|
|
~ |
~ |
~ |
~ |
öèé. Если для заданного набора n векторов P1 |
; P2 |
; P3 |
; : : : ; Pn |
||||
~ |
~ |
~ |
~ |
~ |
|
|
|
требуется найти сумму P |
= P1 |
+ P2 |
+ P3 |
+ : : : + Pn, то аналити- |
|||
чески это удобно выполнить следующим образом.
Нужно выбрать прямоугольную систему координат с осями, например x; y и z, и найти проекции каждого из складываемых векторов на эти оси. Проекциями на ось x будут P1x; P2x; P3x; : : : ; Pnx; íà îñü y P1y ; P2y ; P3y ; : : : ; Pny ; íà îñü z P1z ; P2z ; P3z ; : : : ; Pnz :
Проекция суммы векторов на любую ось равна алгебраиче- ской сумме проекций этих векторов на ту же ось (см. формулу (1.54)). Поэтому
Px = P1x + P2x + P3x + : : : + Pnx; |
(1.87) |
||
Py = P1y + P2y + P3y + : : : + Pny ; |
(1.88) |
||
Pz = P1z + P2z + P3z + : : : + Pnz : |
(1.89) |
||
После этого по формуле (1.76) находится модуль суммарного |
|||
вектора |
|
|
|
P = q |
|
; |
|
Px2 + Py2 + Pz2 |
(1.90) |
||
~
а ориентация вектора P определяется направляющими косинусами
|
~ |
|
Px |
~ |
|
Py |
~ |
|
Pz |
|
|
cos ( |
dx |
) = |
P |
dy |
) = |
P |
dz |
) = |
P |
: |
(1.91) |
|
P ; ~e |
|
; cos (P ; ~e |
|
; cos (P ; ~e |
|
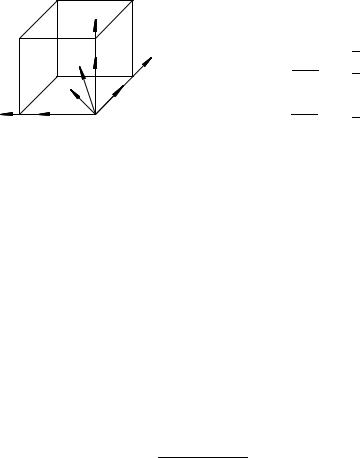
П р и м е р 21. На одну из вершин куба действуют пять численно равных сил таким образом, что три силы направлены вдоль ребер, сходящихся в этой вершине; четвертая сила по диагонали грани, а пятая вдоль диагонали самого куба. Опре-
делить равнодействующую этих сил. |
|
|
|
Решение. Систему координат выберем таким образом, чтобы |
|
|
~ |
~ |
ñèëà F1 была направлена по оси x, сила F2 ïî îñè y, à ñèëà |
||
~ |
ïî îñè z: |
|
F3 |
|
|
|
~ |
направлена по диагонали |
|
Расмотрим случай, когда сила F4 |
|
AC квадрата ABCD (рис. 38), т.е. под углом 45 к осям x и
56 |
|
|
|
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
|||||||||
z и перпендикулярно оси y: Обозначим буквой угол между |
|||||||||||||
векторами |
~ |
|
|
~ |
: |
~ |
|
~ |
|
|
|
|
|
F |
|
è F |
(F5 |
; F4) = : |
|
|
|||||||
|
C0 |
|
5 |
|
4 |
|
|
d0 |
|
Для нахождения проекций силы |
|||
|
|
|
|
|
|
|
B |
|
~ |
, лежащей на диагонали прямоу- |
|||
|
|
|
|
|
|
|
|
|
|
F5 |
|||
D0 |
|
|
y |
A |
0 |
|
|
|
|
гольника AA0C0C, нам потребуют- |
|||
|
|
|
|
|
|
|
ñÿ |
|
p |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
~ |
|
|
z |
|
|
CA |
|
||
|
~ |
|
|
|
|
|
|
|
|
||||
|
|
|
F2 |
|
|
|
|
|
2 |
|
|||
|
F5 |
|
|
|
|
|
|
|
|
cos = C0A = p3 |
; |
||
|
C |
|
|
|
|
~ |
B |
|
|
||||
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
x |
F4 |
|
|
|
|
F3 |
|
|
|
C0C |
1 |
|
|
D |
~ |
|
|
A |
|
|
|
|
|
|
sin = C0A |
= p3 |
: |
|
F1 Ðèñ. 38 |
|
|
|
|
|
|
|
|
|
|||
Так как по условию модули сил одинаковы, то положим их
равными F : F1 = F2 = F3 = F4 = F5 = F . Найдем проекции сил на оси координат x, y; z:
F1x = F; F2x = 0;
F3x = 0;
F4x = F cos 45 ;
F5x = F cos cos 45 ;
F1y = 0; F2y = F; F3y = 0; F4y = 0;
F5y = F sin ;
F1z = 0; F2z = 0;
F3z = F;
F4z = F cos 45 ;
F5z = F cos cos 45 :
Используя формулы (1.87)-(1.90), находим равнодействующую
Rx = F (1 + cos 45 + cos cos 45 ) 2:28F;
Ry = F (1 + sin ) 1:58F;
Rz = F (1 + cos 45 + cos cos 45 ) 2:28F:
Модуль равнодействующей
q
R = Rx2 + Ry2 + Rz2 3:59F:
Здесь все числовые коэффициенты вычислялись с точностью до сотых долей единицы.
Проекции равнодействущей на оси x и z одинаковы, значит
~ |
0 |
0 |
C. Найдем угол между равнодей- |
|||
R |
лежит в плоскости AA |
C |
||||
(R;~ F~4) 63:9 . |
dy |
y |
|
|
||
|
~ |
~ |
|
|
|
0:44, следовательно, |
ствующей R и осью y: cos(R; ~e ) = R =R |
|
|||||
d

Ÿ 7. Вектор в ортонормированном базисе |
57 |
Задачи 28. Найти величину и направление суммы трех векторов в
декартовой системе координат ~v1 = ~e1 + 2~e2 3~e3; ~v2 = 2~e1 +
3~e2 + 1~e3 ; ~v3 = 3~e1 3~e2 + 5~e3 : |
|
|
|
29. |
Вершины треугольника ABC в декартовой системе име- |
||
ют координаты A(2; 1; 1), B( 2; 2; 1), C( 2; 1; 1). Найти ко- |
|||
ординаты точки пересечения биссектрис ABC. |
|
|
|
30. |
В плоскости Oxy даны точки A(1; 3) и B( 3; 2). Найти |
||
|
AB на оси координат. |
|
|
проекции вектора ! |
|
|
|
31. |
В плоскости Oxy даны точки A(2; 1) и B(6; 2). Найти |
||
|
AB с осями Ox и Oy, а также длину этого вектора. |
||
углы вектора ! |
|
|
|
32. |
В плоскости Oxy даны точки A(2; 1); B(5; 3); C(3; 5) и |
||
|
AB è CD. |
|
|
D( 5; 11). Найти угол между векторами ! ! |
|
|
|
33. |
AB на направление векто- |
||
ðà ! |
Найти проекцию вектора ! |
|
|
CD, если известны декартовые координаты точек: A(2; |
|
1); |
|
B( 1; 2); C( 4; 7) è D(1; 5). |
|
||
|
|
||
34. |
В плоскости Oxy даны точки A(3; 5); B(6; 2). Найти |
||
|
AB на ось, направленную из начала коорди- |
||
проекцию вектора ! |
|
|
|
нат по биссектрисе первого координатного угла.
35.Даны три последовательные вершины параллелограмма ABCD: A(1; 2; 3), B(3; 2; 1), C(6; 4; 4). Найти четвертую вершину D.
36.Вектор составляет с осями Ox и Oy углы 60 и 120 : Какой угол он составляет с осью Oz?
37. |
На плоскости |
~ |
Oxy даны три вектора ~a = ~ex ~ey , b = |
||
|
|
~ |
3~ex 2~ey è ~c = 2~ex + 4~ey : Разложить вектор ~c по векторам ~a и b: |
||
38. |
Даны точки A(2; 2; 0) и B(0; 2; 5). Определить длину |
|
|
AB. |
|
вектора ! |
|
|
39. |
Вектор ! |
|
OM = ~r составляет с осями координат равные |
||
острые углыp. Определить координаты вектора ~r, если его длина равна r = 2 3.
40. Радиус-вектор ~r точки M составляет с осями Ox и Oy углы соответственно 45 и 60 . Определить координаты точки M , если r = 6, и координата z отрицательна.
41. Отношение оснований AD и BC трапеции ABCD равно
! ! !
AD=BC = 2. Выразить вектор AD через AB и AC:
58 Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ
42. |
Точка B делит дугу окружности ^AC = 90 â îòíî- |
||
шении 2 : 1. Точка O центр окружности. Разложить вектор |
|||
! |
! |
! |
~ |
OC = ~c по векторам OA = ~a и OB = b. |
|||
43. |
|
|
~ |
Найти угол между векторами b = ~ex 2~ey + 2~ez è ~a = |
|||
~ex + ~ey .
44.Определить углы ABC, если вершины треугольника имеют следующие координаты: A(2; 1; 3); B(1; 1; 1); C(0; 0; 5).
45.Найти угол между диагоналями параллелограмма, по-
~
строенного на векторах ~a = 2~ex + ~ey è b = 2~ey + ~ez .
46. На одну из вершин куба действуют пять численно равных сил таким образом, что три силы направлены вдоль ребер, сходящихся в этой вершине; четвертая сила по диагонали грани, а пятая вдоль диагонали самого куба. Взаимную ори-
~ |
~ |
~ |
~ |
выбрать так, как показано на рис. |
||||
ентацию сил F1 |
, F2 |
, F3 |
è F5 |
|||||
38, а для направления силы |
~ |
|
|
|
|
|||
F4 рассмотреть две возможности: |
||||||||
1) вдоль диагонали AD0, 2) вдоль диагонали AB0. Определить |
||||||||
равнодействующую этих сил. |
|
|
|
|
||||
|
|
|
|
~ |
~ |
~ |
~ |
~ |
47. В плоскости Oxy заданы пять векторов f1 |
, f2 |
, f3 |
, f4 |
, f5. |
||||
Первый вектор направлен по горизонтали вдоль оси Ox вправо (ось Oy направлена вверх), а каждый из остальных образует с ним соответственно углы '2, '3, '4, '5. Определить модуль и направление геометрической суммы этих векторов. Значения fi (i = 1; 2; 3; 4; 5) è 'i, (i = 2; 3; 4; 5) взять из таблицы согласно двузначному номеру варианта mn, первая цифра которого m определяет величины векторов, а вторая цифра n углы. Результаты вычислений округлять до сотых долей единицы.
П р и м е р 22. Решим вариант 00 задачи 47.
Выпишем проекции складываемых векторов на оси Ox и Oy:
f1x = f1 = 2; |
|
|
|
|
|
|
|
f1y = 0; |
|
|
|
|
|
|
|
|
|
||
f2x = 2 cos ( 150 ) 1:73; |
f2y = 2 sin ( 150 ) = 1; |
|
|||||||||||||||||
f |
3x |
= 5 cos 30 |
|
4:33; |
|
f3y = 5 sin 30 |
|
= |
2:5; |
|
|
|
|||||||
f |
= 10 cos ( |
|
|
) |
|
9:66; |
|
|
) |
|
|
2:59; |
|||||||
4x |
|
15 |
|
|
f4y = 10 sin ( |
15 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
f5x = 5 cos ( 75 |
|
) 1:29; |
f5y = 5 sin ( 75 |
|
) 4:83: |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
~ |
~ |
|
|
|
~ |
|
~ |
~ |
|
|
Найдем проекции суммы векторов ~s = f1 + f2 |
+ f3 |
+ f4 |
+ f5 |
|||||||||||||||

Ÿ 8. Скалярное произведение векторов |
59 |
íà îñè Ox è Oy
sx = f1x + f2x + f3x + f4x + f5x sy = f1y + f2y + f3y + f4y + f5y
Длина суммарного вектора q
15:55;
5:92:
|
|
|
|
|
|
|
s = sx2 + sy2 16:64: |
|
|
|
|
|
|||||||||
Направляющие косинусы суммы ~s: |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
d |
|
sx |
|
|
|
|
|
d |
|
sy |
|
|
|
|
|
||
|
|
|
cos(~s; ~ex) = |
s |
0:93; |
|
cos(~s; ~ey ) = |
s |
|
0:36; |
|||||||||||
следовательно, вектор ~s образует с осью Ox угол |
|
21:6 . |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица к задаче 47 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
m |
f1 |
f2 |
|
f3 |
f4 |
|
f5 |
|
n |
'2 |
|
'3 |
|
|
'4 |
|
'5 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
0 |
2 |
2 |
|
5 |
10 |
|
5 |
|
0 |
150 |
|
30 |
|
15 |
75 |
||||
|
|
1 |
3 |
4 |
|
4 |
9 |
|
6 |
|
1 |
30 |
|
60 |
|
45 |
|
135 |
|||
|
|
2 |
4 |
6 |
|
9 |
8 |
|
7 |
|
2 |
45 |
|
120 |
|
75 |
|
60 |
|||
|
|
3 |
5 |
5 |
|
3 |
7 |
|
8 |
|
3 |
60 |
|
45 |
|
90 |
|
120 |
|||
|
|
4 |
6 |
9 |
|
7 |
6 |
|
9 |
|
4 |
90 |
|
60 |
|
135 |
15 |
||||
|
|
5 |
7 |
12 |
|
12 |
5 |
|
11 |
|
5 |
120 |
|
45 |
|
60 |
30 |
||||
|
|
6 |
8 |
3 |
|
3 |
4 |
|
2 |
|
6 |
135 |
30 |
|
15 |
60 |
|||||
|
|
7 |
9 |
15 |
|
8 |
7 |
|
3 |
|
7 |
150 |
|
15 |
|
30 |
|
60 |
|||
|
|
8 |
10 |
10 |
|
8 |
7 |
|
4 |
|
8 |
180 |
|
45 |
|
150 |
75 |
||||
|
|
9 |
11 |
7 |
|
15 |
3 |
|
5 |
|
9 |
60 |
|
75 |
|
30 |
|
150 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ÿ 8. Скалярное произведение векторов
~
С к а л я р н о е п р о и з в е д е н и е векторов ~a и b это чис-
~
ло, обозначаемое символом ~a b (точка между векторами знак скалярного умножения) и равное произведению модулей перемножаемых векторов и косинуса угла между ними
~ |
~ |
(1.92) |
|
~a; b): |
|
~a b = ab cos(d |
|
|
Используя определение проекции вектора на ось, скалярное произведение двух векторов можно записать в виде
~ |
(1.93) |
~a b = aba = bab: |
~
Очевидно, что два ненулевых вектора ~a и b взаимно перпен-
дикулярны тогда и только тогда, когда ~
~a b = 0.
60 |
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
8.1. Cвойства скалярного произведения. Согласно определению (1.92), скалярное произведение обладает переместительным свойством
~ ~ |
(1.94) |
~a b = b ~a; |
так как ни модули векторов, ни косинус угла между ними не зависят от такой перестановки множителей.
Сочетательное относительно числового множителя свойство скалярного произведения следует из свойства (1.55) проекции вектора на ось и формул (1.93) и (1.94):
~ |
~ |
(1.95) |
( ~a) b = b( a)b = bab = (~a b): |
||
Формулы (1.93), (1.94) и (1.54) позволяют легко доказать распределительное свойство скалярного произведения относительно суммы векторов:
~ |
~ |
~ |
(~a + b) ~c = ~c (~a + b) = cac + cbc = ~c ~a + ~c b = |
||
|
~ |
(1.96) |
|
= ~a ~c + b ~c: |
|
Первое и четв¼ртое равенства в этой формуле есть следствия свойства (1.94), третье - формулы (1.93), а второе равенство обосновывается ранее доказанным свойством (1.54) проекции суммы векторов на ось, а именно: проекция суммы равна сумме проекций.
По определению (1.92) скалярного произведения
0; |
åñëè ~a |
|
нулевой вектор, |
(1.97) |
~a ~a = a2 > 0; |
åñëè ~a |
ненулевой вектор. |
||
|
|
|
|
|
П р и м е р 23. Проверить, справедливы ли следующие равенства:
|
2 |
; |
|
|
~ ~ |
|
|
2 |
; |
|
|
|
|
|
|
|
|
1) ~aa = a |
|
|
5) ~a(b b) = ~ab |
|
|
|
|
|
|
|
|
||||||
2 |
|
3 |
; |
~ |
2 |
= a |
2 |
+ b |
2 |
|
|
~ |
|||||
2) ~a |
a = a |
|
6) (~a b) |
|
|
|
|
2~a b; |
|||||||||
2 |
|
3 |
; |
~ |
|
|
|
~ |
|
|
|
2 |
2 |
; |
|||
3) a ~a = a |
7) (~a + b) (~a b) = a |
|
b |
||||||||||||||
|
~ |
|
|
2~ |
~ |
2 |
|
2~ |
2 |
: |
|
|
|
|
|
||
4) ~a(~a b) = a b; |
8) (~a b) |
|
= ~a b |
|
|
|
|
|
|||||||||
