Беляев Ю.Н. Введение в векторный анализ

~

ãäå Fj равнодействующая всех сил, приложенных к j-й материальной точке. Следовательно,

центр масс системы движется как точка, в которой сосредоточена вся масса системы и к которой приложен главный вектор внешних сил, действующих на систему.

Если система изолированная, т.е. главный вектор внешних сил равен нулю, центр масс согласно полученной формуле не изменяет своего движения, другими словами находится в покое или движется прямолинейно и равномерно.

Ф о р м у л а д л я п р о и з в о д н о й с к а л я р н о г о п р о и з- в е д е н и я. Используя свойства скалярного произведения представим приращение скалярного произведения вектор-функций

где последнее слагаемое второго порядка малости по сравнению с первыми двумя.

~ ~

Разделим найденное выражение для (f1 f2) на приращение аргумента и возьмем предел от разностного отношения

84 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА

Отметим три важных следствия формулы (2.8).

Если вектор ~ изменяется в зависимо-

Ñ ë å ä ñ ò â è å 1. f ( )

сти от только по направлению (то есть модуль вектора есть величина постоянная f = const), то

Скалярное произведение двух ненулевых векторов равно нулю, если они взаимно ортогональны. Таким образом, последнее равенство доказывает соотношение (2.9).

С л е д с т в и е 2. Для производной модуля вектор-функции

Здесь для производных использована сокращенная форма за-

Такие обозначения будем использовать и в дальнейшем. Преобразуем формулу ( ), используя равенство (2.10)

доказывается точно та же, как и (2.8).

П р и м е р 38. Теорема об изменении момента импульса м.т. По определению, момент импульса материальной точки есть

векторное произведение е¼ радиус-вектора на импульс м.т.

_

По определению (2.2), ~r = ~v, поэтому первое слагаемое в правой части последней формулы равно нулю. Второе слагаемое преобразуем, используя второй закон Ньютона

это момент сил, действующих на м.т., относительно центра O, из которого проводится радиус-вектор ~r.

86 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА

Для доказательства равенства (2.14) и (2.15) нужно последовательно применить правила (2.8) и (2.11).

Ф о р м у л а Т е й л о р а, дающая разложение вектор-функ- ции в ряд по возрастающим степеням приращения аргумента, имеет такой же вид, что и для скалярной функции:

~

Обозначим разность между f ( ) и суммой n + 1 первых членов ряда (2.17) через ~"n( ). Для того чтобы при некотором значе- нии имело место разложение (2.17), необходимо и достаточно, чтобы

lim ~"n( ) = 0:

!0

Доказательство формулы (2.17) выполняется точно так же, как и ее скалярного аналога.

Ê î î ð ä è í à ò í î å ï ð å ä ñ ò à â ë å í è å ï ð î è ç â î ä í î é. Åñ-

~ ~ ~

ли базисные векторы b1, b2, b3 не зависят от скалярного параметра , то вычисление производной вектор-функции по скалярному аргументу сводится к вычислению производных ее

i=1

и отношение приращения векторной функции к приращению скалярного аргумента можно записать в виде

Если функции f1( ), f2( ), f3( ) имеют производные при выбранном значении , то множители при базисных векторах в пределе при ! 0 обратятся в производные dfd 1 , dfd 2 ; dfd 3 и из последнего равенства получим формулу (2.18).

П р и м е р 39. Скорость и ускорение м.т. в декартовой системе координат.

Радиус-вектор ~r, скорость ~v и ускорение ~a, как и любой другой вектор, могут быть разложены на составляющие. Например, если с началом системы отсчета т. O связана прямоугольная система координат OXY Z (рис. 52), то радиус-вектор ~r можно записать в виде

ãäå ~ex; ~ey ; ~ez единичные базисные векторы декартовой системы координат OXY Z, а x; y; z проекции радиус-вектора ~r на координатные оси.

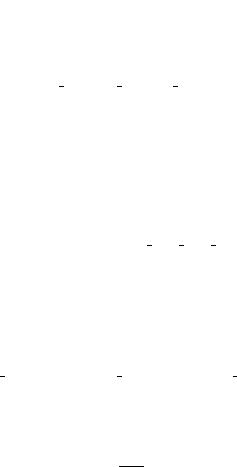
88 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА

Аналогично, обозначив через vx, vy , vz è ax; ay ; az проекции скорости и ускорения на координатные оси X; Y; и Z, имеем

Дифференцируя левую и правую части формулы (2.19) по времени и считая ориентации координатных осей неизменными, с учетом определения (2.2) получаем

Сравнивая формулы (2.20) и (2.22), находим выражения для проекций скорости на оси прямоугольной декартовой системы координат

Точно так же для проекций ускорения можно получить

Направления векторов скорости ~v и ускорения ~a в декартовой системе координат определяются направляющими косинусами:

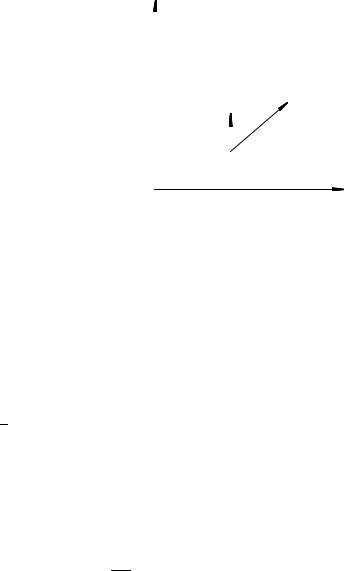
П р и м е р 40. Движение м.т. задано радиус-вектором

~r = At~ex + Bt2 2 ~ey ;

где t измеряется в секундах, постоянная A в м/с, и постоянная B в м/с2: Определить уравнение траектории, величину и направление скорости и ускорения м.т. в момент времени t = 1 с:

Решение. Согласно условию задачи,

а по формулам (2.24) и (2.27) ускорение

~a = B~ey ; a = jay j = jBj:

При условии A = 1м/с и B = 1 м/c2 имеем следую-

щие значения искомых величин для момента времени t = 1с: p

v(1) = 2(ì/ñ); a(1) = 1(ì/ñ2); направления векторов ~v и ~a в момент времени t = 1 с показаны на рис. 53. Ускорение остается неизменным для любого момента времени t.

Ÿ 2. Интеграл от вектора

Åñëè

~

dF ~ d = f;