Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сыктывкарский Государственный Университет им. Питирима Сорокина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Беляев Ю.Н. Введение в векторный анализ

.pdf

Скачиваний:

401

Добавлен:

29.03.2016

Размер:

1.13 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2215 16 17 18 19 20 21 22 > Следующая >>>

Ÿ 1. Скалярное поле

141

линии, построенные с тем же интервалом 1=12 и отмеченные на рисунке цифрами 1, 2, ..., 7. Нулевым потенциалом обладают точки прямой 4.

1.6. Градиент сложной функции. Пусть в области заданы дифференцируемые скалярные поля U1(M ); U2(M ); : : : ; Un(M ) è (M ) = (U1(M ); U2(M ); : : : ; Un(M )):

Используя формулы (3.5) и (3.7), находим

	@			@
grad (U1; : : : ; Un) =		grad U1	+ : : : +		grad Un:
	@U1			@Un
В частности,

grad (c1U1 c2U2)			= c1grad U1 c2grad U2;
grad (U1U2)			= U1grad U2 + U2grad U1;
	U2			U22
grad		U1	=	U2grad U1 U1grad U2	;

grad (U n)			= n U n 1grad U;

(3.11)

(3.12)

(3.13)

(3.14)

(3.15)

ãäå c1; c2 постоянные.

П р и м е р 57. Рассмотрим поле, зависящее только от расстояния точки до начала координат: U = '(r).

Поверхностями уровня служат концентрические сферы с центром в начале координат. Нормалью к поверхности уровня, проходящей через некоторую точку M , является радиус-вектор этой точки. Поэтому градиент поля '(r) по модулю равен

jgrad '(r)j =	@r	:
	@'(r)

Градиент поля направлен в сторону возрастания поля. Ес-

ëè @'(r) > 0, направление градиента определяется единичным

вектором ~er = ~r=r: При отрицательном значении производной

@'(r)	градиент направлен по ~er . Следовательно,
@r	градиент направлен по ~er . Следовательно,
	grad '(r) =	@'	~er :	(3.16)

		@r

142

Глава 3. ФУНКЦИИ ТОЧКИ

П р и м е р 58. Найд¼м производную по направлению поля

сферической волны

'(r) = A

eikr

;

где A и k постоянные, i мнимая единица.

По формулам (3.5) и (3.16) находим

eikr

= A

~er ~e` = A

cos(~er ; ~e`): (3.17)

П р и м е р 59. Градиент электростатического поля точеч-

ного заряда.

grad

~r:

Полученный вектор есть напряж¼нность электростатического поля точечного заряда.

П р и м е р 60. Рассмотрим на плоскости скалярное поле ' = r1 + r2, ãäå r1 è r2 расстояния переменной точки до двух фиксированных точек (фокусов) F1 è F2.

Линиями уровня для данной функции являются эллипсы

					r1 + r2 = const = 2a;
			grad '		где a большая полуось эллипса.
	~r1				Следовательно, вектор
		r1	~r2		Следовательно, вектор
		r1	~r2
				r2	~r1	~r2
			r1		~r1	~r2
	r2		r1		grad ' = r1	+ r2

					определяет нормаль к эллипсу. Оче-
					определяет нормаль к эллипсу. Оче-
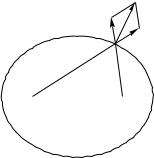
F2			F1		видно, grad ' направлен по диагона-
					ли ромба (см. рис. 83), построенно-
					го на единичных векторах ~r1=r1 è
	Ðèñ. 83				~r2=r2, и делит угол между радиус-
					векторами ~r1 è ~r2 пополам.

Вследствие этого свет от точечного источника, помещ¼нного в фокусе F1, отражаясь от зеркальной эллиптической поверхности, собер¼тся в точке F2 (угол падения равен углу отражения).

Ÿ 1. Скалярное поле

143

П р и м е р 61. Требуется найти такую точку M (~r), сумма квадратов расстояний которой до заданных n точек Mi(~ri) (i = 1; 2; : : : ; n) минимальна.

Обозначим через Ri (i = 1; : : : ; n) радиус-векторы, прове-

д¼нные из точки M в Mi: Ri = ~ri ~r. Рассмотрим функцию

' = i=1 R~ i 2 :		( )
n
X

В окрестности искомой точки M , где эта функция должна быть минимальна, поверхности уровня должны быть замкнутыми и охватывающими точку M , так что в самой точке должно выполняться

grad ' = 0:

( )

Подставляем функцию ( ) в формулу ( ) и выполним вы- числения по правилу (3.11). Получаем

2 R~ 1	R~	1	+ : : : + 2 R~ n	R~ n	= 0:
	~			~
	R1			Rn

Разрешая это уравнение относительно радиус-вектора ~r точки M , находим

1 Xn

~r = n i=1 ~ri:

1.7. Градиент в ортогональной системе координат.

Элементарное смещение d`j вдоль j-ой координатной линии равно

d`j = Hj dqj ;

ãäå qj è Hj обобщенная координата и коэффициент Ламе для рассматриваемой оси.

В соответствии с определением (3.5) проекция grad U на ось qj , определяемую единичным вектором ~ej , равна

gradj U =	@U	=	1 @U	; j = 1; 2; 3;

	@`j		Hj @qj

144	Глава 3. ФУНКЦИИ ТОЧКИ

и, соответственно, сам вектор grad U в ортогональной криволинейной системе координат выражается формулой

1 @U

(3.18)

grad U =

~e1 +

~e2

~e3:

@q1

@q2

@q3

Ï ð è ì å ð 62. Ã ð à ä è å í ò

â ä å ê à ð ò î â î é

ñ è ñ ò å ì å

к о о р д и н а т вычисляется по формуле

(3.19)

grad U =

~ex

~ey +

~ez ;

которая следует из (3.18), если в последней сделать подстановку всех величин применительно к декартовой системе координат:

q1 = x;		~e1	= ~ex;
q2	= y;	~e2	= ~ey ;
q3	= z;	~e3	= ~ez ;

H1 = Hx = 1; H2 = Hy = 1;

H3 = Hz = 1:

Получим формулу для градиента в декартовой системе координат ещ¼ раз, теперь непосредственно из определения градиента (3.1). В декартовой системе координат XY Z с ортонормированным базисом ~ex; ~ey ; ~ez для дифференцируемого скалярного поля U; согласно определению (3.1), можем записать

U = Gx x + Gy y + Gz z + (`);

ãäå Gx; Gy ; Gz и x; y; z есть проекции соответственно векторов grad U и ~r на оси координат.

Из последнего равенства и определения производной по направлению (3.5) находим, что проекции градиента скалярного поля на оси декартовой системы координат равны частным производным поля по соответствующим координатам:

grad xU =

; grad y U =

;

grad z U =

;

(3:190)

и модуль градиента, следовательно, равен

jgrad U j = s @x

+ @y

(3.20)

Ÿ 1. Скалярное поле

145

П р и м е р 63. Докажем равенство (3.16) непосредственным вычислением по формулам (3.11) и (3.19).

В декартовой системе координат

r = x2 + y2 + z2:

Находим

grad '(r) = @'@r grad r;

grad r =

~ex

~ey +

~ez =

(x ~ex + y ~ey + z ~ez ) =

= ~er :

x2 + y2 + z2

Поэтому

grad '(r) =

~er :

Предположим, что

тогда

3~r

' =

;

grad '(r) =

П р и м е р 64. Найти производную плоского скалярного поля U (x; y) = 3x3 xy + y2 в точке M (1; 2) по направлению, идущему от этой точки к т. N (5; 5):

Решение. По формуле (3.19) находим

grad U (x; y) = (9x2 y)~ex + (2y x)~ey :

!	x	y		è	~e` =	4	~ex +	3	~ey :
						5		5
M N = 4~e		+ 3~e	;

Следовательно, производная по направленю ` существует для всех точек плоскости XY :

@U	= grad U (x; y) ~e	=	36x2 3x + 2y	;	и в точке M:	@U	= 7:4 :
@`			5			@`
	`

146	Глава 3. ФУНКЦИИ ТОЧКИ

Задачи 83. Найти линии (поверхности) уровня скалярного поля:

1) U (x; y) = 2x + y;

U (x; y) = x

+ y2

2) U (x; y) = x y;

4) U (x; y; z) = x

+ y

84. Вычислить градиент скалярного поля U (M ):

1) U (x; y; z) = x2 + 4y2 + 9z2;

6) U (r) = ln r;

U (x; y; z) = xyz;

7) U (~r) = (~c ~r)2; 2

;

U (x; y; z) = exyz ;

8) U (~r) = r2(~c ~r)

;

4) U (M ) = r

9) U (r) = (b ~r) (~c ~r);

U (r) = sin br;

10) U (~r) = ~ex (~ey ~r);

где ~r радиус-вектор точки M (x; y; z), r =

x2 + y2 + z2

постоянные векторы.

длина радиус-вектора точки, ~c и b

85.Дано скалярное поле '(~r). Написать векторное уравнение нормали к поверхности уровня поля '(~r), проходящей через точку M0(~r0).

86.Дано скалярное поле '(~r). Написать векторное уравнение плоскости, касательной к поверхности уровня поля '(~r),

проходящей через точку M0(~r0).

87.Гипербола r1 r2 = 2a (r1 è r2 расстояния точки гиперболы до двух фокусов) являются линиями уровня для ска-

лярного поля ' = r1 r2. Доказать, что нормаль к гиперболе делит пополам угол между радиус-векторами ~r1 è ~r2.

88.Материальная точка массой m, имеющая координаты x0; y0; z0, создает вокруг себя поле сил тяготения. Показать, что напряженность этого поля в точке M (x; y; z) является градиентом скалярного поля

' = m=r;

ãäå r = (x x0)2 + (y y0)2 + (z z0)2:

89. Дано скалярное поле U . Найти: 1) градиент данного по-

ля в точке M ; 2) производную поля U по направлению M N в точке M (результат вычислений округлить до сотых долей единицы); 3) уравнение плоскости, касательной к поверхности

Ÿ 1. Скалярное поле

147

уровня поля U в точке M . Значения координат точек M и N и функциональную зависимость скалярного поля U взять из таблицы согласно двузначному номеру варианта mn, первая цифра которого m определяет координаты x, y, z точек M и N , а вторая цифра n функциональную зависимость скалярного поля U от координат.

Таблица к задаче 89

m	M	N	n	U (x; u; z)
m	x; y; z	x; y; z	n	U (x; u; z)
	x; y; z	x; y; z

0	1, 1, -1	7, 3, 2	0	x2yz + 2xy2z
1	1, 2, 1	2, 4, 3	1	2yz + xy2z
2	1, 2, 1	1, 0, -1	2	3x2z 2xy2z
3	-2, 2, -1	3, 2, -2	3	xy2z + x2y2z
4	-1, 4, 3	-1, -2, -1	4	xz3 2x2z
5	-1, -2, 1	1, 2, 1	5	x2y2z 3xyz
6	1, 0, -1	2, 2, 1	6	2x2yz 2xy2z
7	1, 1, 1	-3, -2, 2	7	x2yz + 2xy2z
8	4, 2, 0	1, 2, -3	8	x3yz xy2z
9	-2, 2, 3	5, -2, 3	9	4x2yz + xyz2

Например, для варианта 00:

M (1; 1; 1), N (7; 3; 2), U = x2yz + 2xy2z:

П р и м е р 65. Решим вариант 00 задачи 89.

1) По формуле (3.19) вычисляем градиент поля:

grad U = (2xyz + 2y2z)~ex + (x2z + 4xyz)~ey + (x2y + 2xy2)~ez :

Подставляя сюда координаты точки M , находим:

grad U (M ) = 4~ex 5~ey + 3~ez :

2) Вычитая из координат точки N соответствующие коор-

динаты точки M , получаем координаты вектора M N :

M N = 6~ex + 2~ey + 3~ez :

148

Глава 3.

ФУНКЦИИ ТОЧКИ

Следовательно, единичный вектор в направлении из точки M

â N

M N

~eM N =

~ex +

~ey +

~ez :

M N

j!j

По формуле (3.5) вычисляем производную по направлению

M N :

(M ) = grad U (M )

~eM N

4 6 5 2 + 3 3

3:57:

@`M N

3) Для составления уравнения касательной плоскости воспользуемся формулой (1.105). Получим: 4x + 5y 3z = 12.

Ÿ 2. Векторное поле

Если в каждой точке M области определено значение

некоторой векторной величины P (M ), то говорят, что в области определено векторное поле этой величины. Векторное поле можно рассматривать как вектор-функцию радиус-вектора ~r

~	~	~
точки M : P	= P	(M ) = P (~r); или как вектор-функцию трех ска-

лярных переменных кординат т. M . Например, в декартовой системе координат

~ ~

P = P (x; y; z) = Px~ex + Py~ey + Pz~ez ;

ãäå Px; Py ; Pz функции координат x; y; z т. M .

Для наглядного изображения векторного поля используют-

ся векторные линии, во всякой точке которых вектор поля P направлен по касательной к линии.

2.1.Уравнение векторной линии. Выберем на век-

торной линии, проходящей через точку M (x; y; z), другую точ-

0	0	0	0	). Пусть		~0	радиус-векторы точек M и M		0
êó M	(x	; y	; z	). Пусть		~r è r	радиус-векторы точек M и M
(ñì. ðèñ. 84).
Если точки M и M 0						расположены очень близко друг к другу,
				~0				~
то вектор d~r = r					~r коллинеарен P , т.е.
							~	~
						d~r P		= 0:

Ÿ 2. Векторное поле

149

Перепишем это равенство в декартовой системе координат:

(dy Pz dz Py )~ex + (dz Px dx Pz )~ey + (dx Py dy Px)~ez = 0:

Последнее равенство должно выполняться для любой точки M , что возможно, если нулю равны все три выражения в круглых скобках, т.е.

M		~		dy Pz dz Py = 0;
M			P	dy Pz dz Py = 0;
~r		M 0		dz Px dx Pz = 0;
	~	M 0		dz Px dx Pz = 0;
	0

	r	dx Py dy Px = 0;
	Ðèñ. 84	dx Py dy Px = 0;
	Ðèñ. 84

откуда получаем дифференциальное уравнение векторных ли-

~
íèé ïîëÿ P (M ):
	dx	=	dy	=	dz	:	(3.21)
	Px	=	Py	=		:	(3.21)
	Px		Py		Pz

Интегрирование уравнений (3.21) вводит две произвольные постоянные, то есть получается двупараметрическая совокупность векторных линий.

П р и м е р 66. Найти векторные линии поля скоростей то- чек твердого тела, вращающегося вокруг неподвижной оси.

Решение. При вращении т.т. скорость его точки, определяемой радиус-вектором ~r, выражается формулой

~v = !~ ~r;

где !~ угловая скорость тела.

Выберем направление вектора !~ за ось z декартовой системы координат, т.е.

!x = 0; !y = 0; !z = !:

Тогда

~v = !y~ex + !x~ey :

Дифференциальное уравнение векторных линий имеет вид

!ydx = !xdy = dz0 :

150					Глава 3. ФУНКЦИИ ТОЧКИ
Из последнего равенства находим
	x dx = y dy;				dz = 0;
откуда	x2		y2

		+		= C12;	z = C2:
2
		2

Векторные линии, определяемые этими уравнениями, это

концентрические окружности с центрами на оси z и радиусами p

R = 2C1 (C1 > 0); лежащие в плоскости z = C2 = const: П р и м е р 67. Найти уравнение векторной линии поля

P = A~ex + By~ey + Cz~ez ;

проходящей через т. M0(x0; y0; z0), где A, B, C постоянные. Решение. Дифференциальное уравнение векторных линий

dxA = Bydy = Czdz :

Интегрируя эти уравнения, находим

B
	x = ln jyj + ln C1	;	)
A
C
	x = ln jzj + ln C2	;	)
A

C1y = exp	A x		;
		B
C2z = exp	A x		:
		C

Постоянные интегрирования C1 è C2 находим из условия, что кривая должна пройти через точку M0 с координатами x0; y0; z0. Следовательно,

C1 = y0

exp A x0

;

C2 = z0

exp

A x0

Параметризуем кривую: x = t, тогда

y(t) = y0 exp A (t x0)

;

z(t) = z0 exp A (t x0)

;

и уравнение векторной линии

A (t x0)

~r = t~ex + y0 exp A (t x0)

~ey + z0 exp

~ez :

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2215 16 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.03.2016149.5 Кб11Б3.Б.4.4 ИЗЛ 1-й пол 19 в..doc
#
08.11.2018817.66 Кб31Банковское Дело - курс лекций.doc
#
03.05.2019729.6 Кб12Банковское дело ЛЕКЦИИ.doc
#
18.11.20183.4 Mб10Барулин В.С. - СОЦИАЛЬНАЯ ФИЛОСОФИЯ.doc
#
04.11.2018187.9 Кб12баскетбол ФГОС.doc
#
29.03.20161.13 Mб401Беляев Ю.Н. Введение в векторный анализ.pdf
#
16.11.20191.43 Mб14Беляева Теория вероятностей методичка 2006.doc
#
28.03.2016746.5 Кб26БЖД.doc
#
30.07.2019119.3 Кб1БЖД.doc
#
15.07.20193.68 Mб5Библер В.С. - ОТ НАУКОУЧЕНИЯ - К ЛОГИКЕ КУЛЬТУР....rtf
#
28.03.20169.12 Mб21Бизнес план.doc