
Беляев Ю.Н. Введение в векторный анализ
.pdf
Ÿ 3. Оси естественного тр¼хгранника |
91 |
П р и м е р 41. Закон равнопеременного движения.!
Если м.т. движется с постоянным ускорением ~a = const, то, интегрируя уравнение
d~vdt = ~a;
находим
~v = Z |
~a dt + |
! |
0 |
+ ~at; |
(2.35) |
|
|
const = ~v |
|
ãäå ~v0 скорость м.т. в начальный момент времени t = 0.
_
Используя определение скорости ~v = ~r и интегрируя теперь по времени уравнение (2.35) с уч¼том того, что ~v0 является величиной постоянной, находим
|
~at2 |
(2.36) |
~r = ~r0 + ~v0t + |
2 : |
Здесь ~r0 радиус-вектор материальной точки в начальный момент времени.
Ÿ 3. Оси естественного тр¼хгранника
Рассмотрим пространственную кривую, описанную радиус-
!
вектором ~r = OM , начало которого совпадает с началом координат точкой O, а концом является некоторая точка M (x; y; z). (см. рис. 54).
|
M2 |
M3 |
|
|
M1 |
Mn 1 |
|
|
|
||
M0 |
Ðèñ. 54 |
|
M |
Возьмем на кривой M0M точки M0, M1, M2, : : :, Mn 1, M и, соединив их отрезками, получим ломаную линию
M0M1M2 : : : Mn 1M: (2.37)
Длиной s дуги M0M называется предел, к которому стремится длина ломаной при стремлении к нулю наибольшей из
92 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
длин отрезков Mi 1Mi ломаной (2.37), если этот предел существует и не зависит от выбора точек ломаной (2.37).
При движении переменной точки M (x; y; z) по кривой длина дуги s изменяется, и, обратно, при изменении s изменяются координаты x,y,z точки M , лежащей на кривой. Следовательно, координаты x, y, z точки M можно рассматривать как функции длины дуги s
x = x(s); y = y(s); z = z(s);
и радиус-вектор ~r будет функцией длины дуги s: ~r = ~r(s). Обозначим через ~e единичный вектор касательной к кри-
вой ~r(s) в точке M (s). Этот вектор определяется формулой
|
|
d~r |
|
|
(2.38) |
|
|
~e = ds |
: |
|
|
|
|
~eb(s) |
|
|
|
M0 |
|
M |
|
~e (s) |
|
s |
|
|
|
|
|
|
s |
|
~e (s+ s) |
||
|
|
M 0 |
|||
|
|
|
|
||
|
~r(s) |
|
|
|
|
|
|
|
|
|
|
|
~en (s) |
|
O |
соприкасающаяся |
|
Ðèñ. 55 |
плоскость |
p |
Действительно, производная |
вектор-функции скалярного |
|
аргумента направлена по касательной к годографу этого вектора. Покажем теперь, что длина вектора (2.38) равна единице. При сближении точек M 0 и M длина прямолинейного отрезка M M 0, равная j ~rj, стремится к длине дуги траектории s, заключенной между точками M 0 и M , поэтому
ds |
|
= |
|
|
d~r |
|
|
|
|
|
|
|
|
|
|
s!0 |
|
s |
|
|
|
|
|
|
|
lim |
|
r |
|
= 1: |
|
|
|
|
|
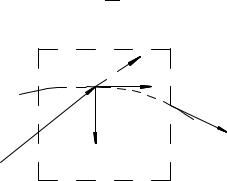
Возьмем другую точку M 0(s + s), лежащую на кривой ~r(s) и близкую к M (s) (рис. 55). Единичный вектор касательной к кривой в точке M 0 будет ~e (s + s).

Ÿ 3. Оси естественного тр¼хгранника |
93 |
Проведем через точки M и M 0 плоскость, содержащую вектор ~e . Предельное положение этой плоскости, получающееся при стремлении M 0 к M ( s ! 0), называется соприкасающейся плоскостью p к пространственной кривой ~r(s) в точке M . В частности, плоская кривая лежит каждой своей точкой в одной соприкасающейся плоскости.
Производная от единичного вектора ~e по длине дуги траектории s, согласно свойству (2.9), перпендикулярна касательной к траектории в точке M и определяет направление главной нормали к траектории в точке M . Очевидно, что единичный вектор главной нормали, который обозначим через ~en, åñòü
~en = |
|
1 |
|
d~e |
: |
(2.39) |
ds |
ds |
|||||
|
|
d~e |
|
|
|
|
|
|
|
|
|
|
|
Введем в точке M единичный вектор бинормали ~eb = ~e ~en, перпендикулярный к соприкасающейся плоскости p. Тогда векторы ~e , ~en è ~eb образуют правую тройку и задают три взаимно перпендикулярных направления, называемые осями естественного трехгранника, или натуральным триэдром. В зависимости от вида пространственной кривой единичные векторы естственного трехгранника могут изменять свое направление, то есть являются функциями параметра s: ~e = ~e (s), ~en = ~en(s), ~eb = ~eb(s). Производные этих вектор-функций по скалярному параметру s определяются формулами Френе2.
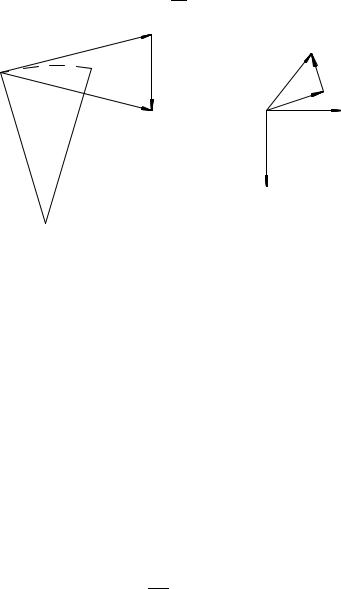
3.1. Формулы Френе. Обозначим угол между единич- ным вектором ~e (s) касательной к траектории в точке M и единичным вектором ~e (s + s) касательной в точке M 0 через ".
Провед¼м из точки M прямую в направлении главной нормали ~en(s). Другую нормаль к кривой провед¼м из точки M 0 перпендикулярно к вектору ~e (s + s) до пересечения с первой (если кривая плоская, то это будет главная нормаль в точке M 0). Обозначим точку пересечения этих нормалей буквой C. По построению (см. рис. 56), 6 M CM 0 = ".
2Жан Френе (J. Frederic Frenet) французский математик (1816-1900).
94 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
При уменьшении длины s дуги M M 0 длины отрезков M 0C и M C стремятся к значению R = lim "s , которое называется
радиусом кривизны кривой в точке M .
Величина K = 1=R = lim " есть кривизна кривой.
s!0 s
~e (s)
|
|
|
|
|
~eb(s + s) |
M |
") |
s |
M 0 |
|
~eb |
|
|
|
|||
|
|
|
~e |
M |
) ~eb(s) |
|
|
|
|
|
|
|
|
|
~e (s + s) |
|
~e (s) |
|
R |
|
|
|
|
|
|
" |
|
|
~en(s) |
|
|
|
|
|
|
|
_ |
|
|
|
|
|
C |
|
|
|
Ðèñ. 57 |
|
Ðèñ. 56 |
|
|
||
|
|
|
|
||
Синус малого угла приближенно |
равен самому углу, т.е. |
||||
sin 2" 2" ; это выполняется тем точнее, чем меньше угол " (приs ! 0 угол " ! 0). Следовательно,
|
ds |
|
= s!0 |
|
s |
|
|
s!0 |
j |
j s |
s!0 s R |
|||||||||||
|
d~e |
|
lim |
|
~e |
|
= lim 2 ~e |
|
sin("=2) = lim |
" = 1 : (2.40) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Объединяя |
|
условия |
(2.39) и (2.40), находим п е р в у ю ф о р- |
||||||||||||||||||
ì ó ë ó Ô ð å í å |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
d~e |
= |
|
1 |
~en: |
|
(2.41) |
||||||
|
|
|
|
|
|
|
|
|
|
ds |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|||||
|
 ò î ð à ÿ ô î ð ì ó ë à Ô ð å í å |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
d~eb |
|
1 |
|
|
(2.42) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
~en; |
|
||||||||
|
|
|
|
|
|
|
|
|
ds |
T |
|
|||||||||||
где T радиус кручения кривой, доказывается аналогично формуле (2.41).
Заметим, что
d~eb
ds ? ~eb:

Ÿ 3. Оси естественного тр¼хгранника |
95 |
Далее, согласно определению вектора ~eb и правилу (2.11) дифференцирования векторного произведения,
|
d~eb |
= |
d(~e ~en) |
= |
d~e |
|
|
~e |
|
+ ~e |
|
d~en |
= ~e |
|
|
d~en |
; |
|||
|
ds |
|
ds |
n |
ds |
ds |
||||||||||||||
|
|
|
|
ds |
|
|
|
|
|
|||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d~eb |
? ~e : |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
|||||
Вектор |
d~eb |
одновременно перпендикулярен ~eb |
è ~e , òî åñòü |
|||||||||||||||||
ds |
||||||||||||||||||||
направлен вдоль оси главной нормали. Это означает, что при движении точки по кривой соприкасающаяся плоскость поворачивается около касательной к кривой. Если при возрастании s соприкасающаяся плоскость поворачивается в направлении от ~en ê ~eb, угол поворота положительный, в противном случае отрицательный.
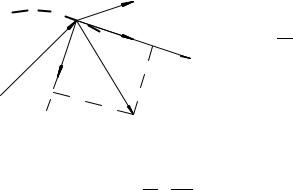
Обозначим угол между бинормалями в точках M и M 0 ÷å-
ðåç |
(см. рис. 57). Кручением кривой называется |
lim |
|
|
|
, à |
|||||||||||||||||
|
s |
||||||||||||||||||||||
величина обратная кручению есть радиус кручения |
|
s!0 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
T = lim |
s |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
s!0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
d~eb |
= |
lim |
~eb |
|
= lim |
|
2 ~eb |
sin( =2) |
= |
|
lim |
|
|
|
|
|
1 |
|
|
|||
ds |
|
|
|
j j |
|
s |
|
s T : |
|||||||||||||||
s!0 j s j |
s!0 |
|
|
|
s!0 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При положительном кручении векторы ~e |
n |
è d~e |
b |
направле- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ны в противоположные стороны, поэтому во второй формуле Френе (2.42) стоит знак (-).
Т р е т ь я ф о р м у л а Ф р е н е выражает производную вектора ~en по параметру s. Используя соотношение ~en = ~eb ~e и формулы (2.41) и (2.42), находим
d~en
ds
= d(~eb ~e ) ds
1
= T ~en ~e
= |
d~eb |
~e + ~eb |
d~e |
= |
|
||||||
ds |
ds |
|
|||||||||
1 |
|
1 |
|
|
1 |
|
(2.43) |
||||
+ |
|
~eb ~en = |
|
~eb |
|
~e : |
|||||
R |
T |
R |
|||||||||

96Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
3.2.Скорость и ускорение в осях натурального триэдра. Отметим на траектории начальное положение м.т. M0 и положительное направление отсчета. Скалярная функция времени s(t) задает длину дуги траектории от начала отсчета M0 до того места M; где в данный момент времени t находится м.т. За бесконечно малый интервал времени dt м.т. совершает перемещение d~r; направленное по касательной к траектории, причем jd~rj = jdsj:
Найдем компоненты скорости и ускорения материальной точки в осях натурального триэдра.
Используя определение скорости материальной точки, правило дифференцирования (2.16) сложной вектор-функции и определение единичного вектора касательной к траектории
(2.38), находим |
|
|
|
|
|
|
|
|
|
~ = |
d~r |
= |
d~r ds |
= |
ds |
~e : |
(2.44) |
||
|
|
|
|
|
|||||
dt |
ds |
dt |
dt |
||||||
Таким образом, вектор скорости всегда направлен по касательной к траектории и по абсолютной величине равен производной
от пути по времени |
= j j = |
dt |
: |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ускорение материальной точки |
найдем, продифференциро- |
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||
вав выражение (2.44) по времени |
|
|
|
|
|
|
|
|
|
|||||||||
|
d2s |
|
ds d~e ds |
|
|
d |
|
2 |
(2.45) |
|||||||||
~a = |
|
~e + |
|
|
|
|
|
|
|
|
= |
|
|
~e + |
|
~en: |
||
dt2 |
dt |
|
ds |
dt |
|
dt |
R |
|||||||||||
Величина |
|
|
|
|
|
dv |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = |
|
= v = s• |
|
|
(2.46) |
|||||||||||
|
|
dt |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
называется тангенциальной составляющей ускорения, a |
|
|||||||||||||||||
|
|
|
an = |
v2 |
|
|
|
|
|
|
|
(2.47) |
||||||
|
|
|
R |
|
|
|
|
|
||||||||||
нормальной составляющей.
Модуль ускорения на основании равенств (2.45-2.47) может
быть теперь записан в виде |
|
|||||
a = qa2 + an2 = s |
|
|
: |
(2.48) |
||
(v)2 + R2 |
||||||
|
|
|
|
v4 |
|
|
Ÿ 3. Оси естественного тр¼хгранника |
97 |
Рассмотрим два частных случая. Если v = const (равномерное движение по траектории), то
a = 0; ~a = an~en
ускорение м.т. (если оно не равно нулю) направлено по главной нормали к траектории.
Если движение прямолинейное, т.е. R = 1, то
an = 0; ~a = a ~e
скорость м.т. изменяется только по величине.
Как видно из формул (2.46) и (2.45), в системе осей натурального триэдра скорость имеет одну составляющую разложения, а ускорение две. В этом состоит преимущество натурального триэдра перед другими системами координат.
П р и м е р 42. Точка движется по окружности радиуса R: Ускорение образует с ее скоростью постоянный угол : Найти зависимость скорости v от времени, если в начальный момент времени t = 0 она равнялась v0:
Решение. Очевидно, что an =6 0 для любого t и, следовательно, v0 =6 0: В противном случае движение было бы по прямой, а не по окружности. По этой же причине 6= 0:
|
|
|
|
|
По условию задачи мож- |
|
M0 |
M |
~eb |
|
|
но записать (см. рис. 58) |
|
|
|
|
|
|
|
|
|
) |
|
~e |
a ~v |
a |
= ctg : |
|
|
|
an |
|||
~r |
|
|
|
|
||
~en |
~a |
|
|
|
|
|
|
|
|
Подставляем в это урав- |
|||
an |
|
|
|
|||
|
|
|
|
нение выражения (2.46) и |
||
O |
|
|
|
|
||
|
|
|
|
(2.47) для тангенциальной и |
||
|
|
|
|
|
||
|
Ðèñ. 58 |
|
|
нормальной составляющих |
||
|
|
|
|
|
ускорения. Получаем |
|
vR2 dvdt = ctg :
После разделения переменных и интегрирования полученного

98 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
уравнения находим
v0
v = 1 v0 t ctg =R :
Åñëè = 90 ; òî v = v0: При < 90 движение по найденному закону возможно в интервале 0 t < R=(v0 ctg ):
П р и м е р 43. Положение материальной точки определяется радиус-вектором:
~r = A cos Bt2~ex + A sin Bt2~ey ;
ãäå A = 3ì; B = 2ñ 2: Найти: уравнение траектории; скорость и ускорение м.т.; закон движения по траектории s(t); отсчитывая расстояние от начального положения точки; тангенциальное и нормальное ускорения; радиус кривизны в момент времени t = 2c:
Решение. 1)Для нахождения уравнения траектории нужно выразить координаты x = A cos Bt2 è y = AsinBt2 друг через друга. Чтобы исключить время из уравнения движения, возведем их в квадрат:
cos2 Bt2 |
= |
x2 |
; |
sin2 Bt2 |
= |
y2 |
; |
|
A2 |
A2 |
|||||||
|
|
|
|
|
|
и сложим. Получим x2 + y2 = A2 материальная точка движется по окружности радиуса R = 3м:
2) Скорость м.т.
x = 2ABt sin Bt2; y = 2ABt cos Bt2;
и, следовательно, v = 2ABt:
Проекции ускорения на оси X и Y равны:
x• = 2AB(sin Bt2 + 2Bt2cos Bt2); y•= 2AB(cos Bt2 2Bt2sin Bt2);
и, следовательно,
a2 = x•2 + y•2 = 4A2B2(1 + 4B2t4):

Ÿ 3. Оси естественного тр¼хгранника |
99 |
|
3) Закон движения по траектории |
|
|
S = Z t v dt = Z t |
2ABt dt = ABt2(ì): |
|
00
4)Тангенциальное ускорение
a = v = 2AB = 12(ì/ñ2):
Значит, нормальная составляющая ускорения
q
an = a2 a2 = 4AB2t2(ì/ñ2):
5) Так как точка движется по окружности, то радиус кривизны у нее в любой момент времени один и тот же, и в данном случае R = 3м: Покажем это еще раз, используя формулу (2.47) для нормального ускорения. Разрешим ее относительно радиуса кривизны траектории
R = v2 = 3(ì); an
что и требовалось показать.
3.3. Вычисление кривизны пространственной кривой. Если уравнение кривой задано в декартовой системе координат ~r = ~r(s) = x(s)~ex + y(s)~ey + z(s)~ez , то ее кривизна, согласно формуле (2.41), может быть вычислена по формуле
K R |
= |
|
ds |
|
|
= |
ds |
ds |
= |
ds2 |
|
= |
|
|
|||||||||||||
|
1 |
|
|
d~e |
|
|
|
|
|
d |
|
d~r |
|
|
|
|
|
d2~r |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
d2x |
|
|
|
y |
|
|
|
|
|
2 |
z |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
d |
|
|
|
|||||||
|
|
= s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
+ |
|
+ |
|
|
: |
(2.49) |
|||||||||||||||||
|
|
ds2 |
ds2 |
ds2 |
|||||||||||||||||||||||
Рассмотрим теперь случай, когда радиус-вектор ~r является функцией произвольного параметра . В этом случае длину дуги s будем рассматривать как функцию параметра . Используя правило (2.16) дифференцирования сложной вектор-функции, имеем
d~r |
= |
d~r |
|
ds |
: |
(2.50) |
|
d |
ds d |
||||||
|
|
|
|||||
100 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
Для упрощения последующих записей некоторых формул, содержащих производные, последние будем обозначать тем же символом, что и сами функции, но с двумя индексами. Порядок производной отмечается числом штрихов, используемых в качестве верхнего правого индекса, а переменные, по которым ведется дифференцирование, используются как нижние правые индексы. Подобная форма записи нами уже использовалась на стр. 85. Например, формула (2.50), таким образом, запишется
â âèäå
~r 0 = ~rs0 s 0:
Умножим обе части этого равенства скалярно на себя и
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
учтем, что d~rds |
= 1. Получаем |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
ds |
2 |
|
0 |
2 |
0 |
2 |
|
|||||
|
d~r |
|
|
= |
; |
èëè |
~r |
|
|
|
= s |
|
: |
(2.51) |
|||
d |
|
d |
|
|
|
|
|||||||||||
Дифференцируем обе части этого равенства по и сокращаем на два:
d |
|
d 2 |
! |
= d d 2 ; |
èëè |
~r |
~r |
= s s : |
(2.52) |
||||
|
d~r |
|
d2~r |
|
|
ds d2s |
|
|
0 |
00 |
0 00 |
|
|
Из формулы (2.50) находим |
|
|
|
|
|
||||||||
|
|
|
|
|
0 |
~r 0 |
|
|
|
|
|||
|
|
|
|
|
|
|
~rs |
= |
|
: |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
Отсюда можно найти вторую производную от радиус-векто- ра ~r по s:
|
|
|
|
|
|
|
|
|
~r |
00 |
= |
~r 00s 0 ~r 0s 00 |
|
: |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
ss |
|
|
s 0 3 |
|
|
|
|
|
|
|||
Подставляем это выражение в формулу (2.49) |
|
|
||||||||||||||||||||
B |
|
s 0 |
|
|
|
|
|
C |
|
|
|
|
|
|
s 0 |
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
~r 0 2 |
s 00 2 |
|
K2= 0 |
~r |
00 s 0 |
|
~r |
|
0 s |
00 |
1= |
|
~r 00 |
2 |
s 0 |
2 |
2~r 00 |
|
~r 0 s 0 s 00 + |
||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
6 |
|
|
: |
|||||||
@ |
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
