Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сыктывкарский Государственный Университет им. Питирима Сорокина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Беляев Ю.Н. Введение в векторный анализ

.pdf

Скачиваний:

401

Добавлен:

29.03.2016

Размер:

1.13 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2021 / 2221 22 > Следующая >>>

Ÿ 8. Теорема Остроградского и связанные с ней формулы 201

риальную точку массы m, выражается формулой

~		M m
F	=	r3	~r :

8.2. Формула для градиента. Положим

~	~
P	= f b;

где f скалярная функция точки M , а b произвольный постоянный вектор. Согласно формуле (3.77)

~	~ ~	~ ~
div P	= div (f b) = b grad f + f div b = b grad f:

Применим теорему (3.93) к данному векторному полю P :

ZZZ

~		ZZ
~		~
grad f dV = b		f d :

Отсюда, вследствие произвольности вектора b, следует формула

ZZZ

ZZ
~	(3.98)
grad f dV = f d :	(3.98)

			~
8.3. Формула для вихря. Если b произвольный по-
стоянный вектор, то по формуле (3.78)
	~	~
	div (~a b) = b rot ~a;
		~	~
и, подставляя в формулу (3.93) вместо P			вектор ~a b, получаем
~	ZZZ	ZZ	~
b	rot ~a dV =	(~a b) d :

Смешанное произведение не изменяется при циклической перестановке векторных множителей, поэтому последнее равенство можно переписать следующим образом:

~	ZZZ	~	ZZ
~		~	~
b		rot ~a dV = b	d ~a :

202	Глава 3. ФУНКЦИИ ТОЧКИ

Эта формула должна выполняться для любого вектора b, что возможно только, если справедливо равенство

ZZZ

ZZ
~	(3.99)
rot ~a dV = d ~a :	(3.99)

8.4. Формулы Грина. Пусть f1 è f2 скалярные функции точки M , дифференцируемые в области V , ограни- ченной поверхностью .

Образуем векторное поле P = f1 grad f2. Используя формулы (3.77) и (3.80), получаем

div (f1grad f2) = f1div (grad f2) + grad f1 grad f2 = = f1r2f2 + rf1 rf2:

По определению производной скалярного поля по направлению (3.5),

~		@f2
grad f2 d = grad f2	~end =		d ;
		@n

это производная скалярного поля f2 по направлению внешней нормали к поверхности .

Следовательно, применение теоремы Остроградского к рас-

			~								ô î ð-
сматриваемому здесь полю P = f1 grad f2 äà¼ò ï å ð â ó þ											ô î ð-
ì ó ë ó Ã ð è í à:					ZZ
ZZZ	r	r r			ZZ			@f2
(f1	2f2 +	f1		f2) dV = f1				@n	d :		(3.100)
V
Â ò î ð à ÿ ô î ð ì ó ë à Ã ð è í à
ZZZ				ZZ		@f2			@f1
(f1r2f2 f2r2f1) dV = f1							f2			d	(3.101)
(f1r2f2 f2r2f1) dV = f1						@n	f2		@n	d	(3.101)

выводится точно так же, как и первая формула Грина; для этого

нужно рассмотреть векторное поле P = f1 grad f2 f2 grad f1.

Ÿ 8. Теорема Остроградского и связанные с ней формулы 203

И н т е г р а л ь н а я ф о р м у л а Г р и н а получается из второй формулы Грина (3.101). Пусть f1 = u некоторая функция, удовлетворяющая условиям теоремы Остроградского в области V , а f2 фундаментальное решение уравнения Лапласа:

f2	= R ; R = q(x xO )2			+ (y yO )2	+ (z zO )2
	1

расстояние между точкой MO (xO ; yO ; zO ) и точкой M (x; y; z).

Функция f2	= 1=R удовлетворяет всем условиям теоремы
Остроградского во всех точках, кроме MO , где она терпит раз-
рыв непрерывности.			Случай 1. Точка MO íàõî-
			Случай 1. Точка MO íàõî-
			дится внутри области V . Выде-
			лим вокруг точки MO шаровую
			область Va радиуса a и поверх-
~ea			ностью a.
MO	~eR	~en	В области V Va, ограни-
a			ченной поверхностями и a,
a			для функций u и 1=R можно
			использовать вторую формулу
			Грина, прич¼м r2(1=R) = 0. Èç
Ðèñ. 98			(3.101) получаем

Z Z Z

V Va

r2u dV = u

d +

1 @u

ZaZ

1 @u

+ u

d a

d a:(3.102)

Преобразуем два последних интеграла в этой формуле. Вы- числяя производную по внешней нормали к области V Va íà

сферической поверхности a, íàéä¼ì

~eR ~ea

a = a2 ;

R a

= grad

~ea a =

è ïî

формуле среднего значения

d a =

u d a = 4 u(M ) ;

(3.103)

ZaZ

204	Глава 3. ФУНКЦИИ ТОЧКИ

ãäå u(M ) значение функции u в некоторой точке M на сферической поверхности a.

По формуле среднего значения

ZaZ

1 @u

ZaZ

= 4 a

(3.104)

d a =

d a

;

в некоторой

ãäå

@u значение нормальной производной @u

точке M на сферической поверхности .

Используя (3.103) и (3.104), перепишем равенство (3.102) в

âèäå

4 u(M ) = 4 a

r2u dV :

@ 1

1 @u

Z Z Z

V Va

В результате предельного перехода a ! 0

R r u dV ;

M !MO ;

@n MO Z Z Z R r u dV !ZZZ

;

V Va

и мы приходим к формуле

4 u(MO ) = u

r2u dV;(3.105)

1 @u

ZZZ

выражающей значение функции u в некоторой точке MO из объ¼ма V через значения функции u и е¼ нормальной производной на поверхности и значения u в объ¼ме V .

Случай 2. Точка MO лежит вне объ¼ма V и поверхности . Из второй формулы Грина следует

0 = u

ZZZ

r2u dV :

@ 1

1 @u

Случай 3. Точка MO принадлежит поверхности , и в этой точке можно построить касательную плоскость к поверхности(рис. 99).

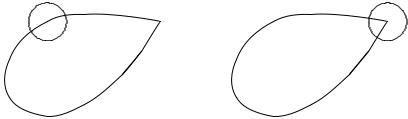
Ÿ 8. Теорема Остроградского и связанные с ней формулы 205

Применим вторую формулу Грина к исходной области за исключением части объ¼ма V , вырезаемого сферой малого радиуса a с центром в точке MO .

В отличие от первого случая, предельное значение формулы (3.103) при a ! 0 да¼т

a!0

u d a = a!0

ZaZ

@ 1

ZaZ

lim

1 2 a2u(M ) =

lim u

= lim 1

= 2 u(MO );

и, соответственно, вместо формулы (3.105) получаем

2 u(MO ) = u

ZZZ

r2u dV :

@ 1

1 @u

Случай 4. Точка MO является вершиной конического выступа на поверхности (рис. 100).

Mo	Mo


Ðèñ. 99	Ðèñ. 100

Результат рассмотрения отличается от формулы (3.105) заменой коэффициента 4 на пространственный угол, под которым внутренность объ¼ма V видна из точки MO .

Объединяя все четыре случая, основную интегральную формулу Грина можно записать в следующем виде:

C u(MO ) = u

ZZZ

r2u dV(3; .106)

@ 1

1 @u

206				Глава 3.	ФУНКЦИИ ТОЧКИ
ãäå
	>	4 ; åñëè MO		V ;
	>
C =	<	2 ; åñëè MO		;		(3.107)
C =	8	2 ; åñëè MO	2	;		(3.107)
	>	; åñëè MO	2	вершина конуса;
	>	0; åñëè MO 2= V; :
	>
	:

В частности, потенциал u лапласова векторного поля в некоторой точке MO выражается через значения функции u и е¼ нормальной производной на поверхности , охватывающей т.

MO :
	1		1 @u			@	1
u(MO ) =					u				d :
u(MO ) =	4		R	@n	u	@n		R	d :
		ZZ

Задачи

107. ~

Доказать, что поток постоянного вектора C через замкнутую поверхность равен нулю:

C d = 0:

108. Доказать следующие формулы:

ZZ	ZZ
~	~
~r d = 3V;	z~ez d = V;
ZZ	ZZ
~	~
x~ez d = 0;	y~ez d = 0;

где V объ¼м, ограниченный замкнутой поверхностью . 109. В декартовой системе координат OXY Z заданы че-

тыре точки O(0; 0; 0); A(2; 0; 0), B(0; 3; 0), C(0; 0; 1). Для силы

F = ( x + z)~ex + (x + y)~ey + (2x + z)~ez вычислить: 1) работу по перемещению по прямой из точки B в точку C; 2) циркуляцию по замкнутому контуру, состоящему из отрезков прямых между точками O, C, A, O; 3) поток через поверхность треугольника OCA в направлении нормали ~ey ; 4) поток через поверхность тетраэдра OABC.

Библиографический список

207

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.А н г о А. Математика для электро- и радиоинженеров/ Пер.с фр. под ред. К.С. Шифрина. 2-е изд. М.: Наука, 1967. 780 с.

2.Б о р и с е н к о А.И., Т а р а п о в И.Е. Векторный анализ и начала тензорного исчисления. Харьков.: Вища школа, 1986. 216 c.

3.К о ч и н Н.Е. Векторное исчисление и начала тензорного исчисления. 9-е изд. М.: Наука, 1965. 427 с.

Êã ë à â å 1

4.И л ь и н В.А., П о з н я к Э.Г. Аналитическая геометрия. 2-е изд. М.: Наука, 1971. 232 с.

5.К у р о ш А.Г. Курс высшей алгебры. 10-е изд. М.: Наука, 1971. 432 с.

6.П о г о р е л о в А.В. Аналитическая геометрия. М.: Наука, 1978. 208 с.

7.Ц у б е р б и л л е р О.Н. Задачи и упражнения по аналитиче- ской геометрии. 29-е изд. М.: Наука, 1968. 336 с.

Êã ë à â å 2

8.Б а т ь М.И., Д ж а н е л и д з е Г.Ю., К е л ь з о н А.С. Теоретическая механика в примерах и задачах. М.: Наука, 1971. Т.1. 512с.

9.К и л ь ч е в с к и й Н.А. Курс теоретической механики. М.: Наука, 1977. Т.1. 480 с.

10.Л о й ц я н с к и й Л.Г., Л у р ь е А.И. Курс теоретической механики. М.: Наука, 1982. Т.1. 352 с.

11.М а р к е е в А.П. Теоретическая механика. М.: Наука, 1990.

416ñ.

12. О л ь х о в с к и й И.И., П а в л е н к о Ю.Г., К у з ь м е н к о в Л.С. Задачи по теоретической механике для физиков. М.: Из-во МУ, 1977. 395 с.

13.П а в л е н к о Ю.Г. Задачи по теоретической механике. М.: Èç-âî ÌÓ, 1988. 344 ñ.

14.П е т к е в и ч В.В. Теоретическая механика. М.: Наука, 1981. 496с.

15.П и с к у н о в Н.С. Дифференциальное и интегральное ис- числения для втузов. 12-е изд. М.: Наука, 1978. Т.1. 456с.

16.П о л я х о в Н.Н., З е г ж д а С.А., Ю ш к о в М.П. Теоретиче- ская механика. Л.: Èç-âî ËÃÓ, 1985. 536 ñ.

208	Библиографический список
17.	Ï ÿ ò í è ö ê è é Å.Ñ., Ò ð ó õ à í Í.Ì., Õ à í ó ê à å â Þ.È.,
	Я к о в е н к о Г.Н. Сборник задач по аналитической меха-
	нике. М.: Наука, 1980. 320 с.

18.Я б л о н с к и й А.А., Н и к и ф о р о в а В.М. Курс теоретиче- ской механики. 5-е изд. М.: Высшая школа, 1977. Часть 1. 368 с.

Êã ë à â å 3

19.Б о л с у н А.И., Г р о н с к и й В.К., Б е й д а А.А. Методы математической физики. Минск: Вышейшая школа, 1988. 199с.

20.И л ь и н В.А., П о з н я к Э.Г. Основы математического анализа. М.: Наука, 1973. Ч.2. 448 с.

21.М а к с в е л л Дж.К. Трактат об электричестве и магнетизме/Пер. с англ. под ред. М.Л. Левина, М.А. Миллера, В.В. Суворова. М.: Наука, 1989. Т. 1. 416 с.

22.М а к с в е л л Дж.К. Трактат об электричестве и магнетизме/Пер. с англ. под ред. М.Л. Левина, М.А. Миллера, В.В. Суворова. М.: Наука, 1989. Т. 2. 437 с.

23.М а к с в е л л Дж.К. Избранные сочинения по теории электромагнитного поля/Пер. с англ. под ред. П.С. Кудрявцева. М.: Гостехиздат, 1954. 687 с.

24.М и с ю р к е е в И.В. Сборник задач по методам математи- ческой физики. М.: Просвещение, 1975. 167 с.

25.П и с к у н о в Н.С. Дифференциальное и интегральное ис- числения для втузов. 12-е изд. М.: Наука, 1978. Т.2. 576с.

26.Ф е й н м а н Р., Л е й т о н Р., С э н д с М. Фейнмановские лекции по физике / Пер. с англ. под ред. Я.А.Смородинского. 3-å èçä. Ì.: Ìèð, 1977. Âûï. 5. 302 ñ.

27.Ф и х т е н г о л ь ц Г.М. Курс дифференциального и интегрального исчисления. 5-изд., М.: Наука, 1969. Т.3. 656 с.

Ответы и решения

209

ОТВЕТЫ И РЕШЕНИЯ

1.~a + b + ~c = 0 (ñì. ðèñ. 9)

2.Формула (1.9) называется неравенством треугольника, геометрическая интерперетация которого состоит в том, что сумма двух

сторон треугольника больше третьей.

						~
	3. Свойство (1.8) очевидно, если один из векторов ~a, b или число
равны нулю. Если векторы ~a и					~	параллельны, то один из них
равны нулю. Если векторы ~a и					b	параллельны, то один из них
						~
можно выразить через другой, например b = a. Тогда свойство (1.8)
следует из (1.7):			~			~
следует из (1.7):			(~a + b) = (~a + ~a) = ~a + ~a = ~a + b:
						~
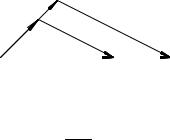
						Пусть ~a и b непараллель-
		~a	~			ные векторы. Тогда при > 0
			~			!
			b			AC изображает, с одной сторо-
	~a	~	b			ны, сумму ~a+ ~a, а с другой
	~a	~				ны, сумму ~a+ ~a, а с другой
		b				!
		~				!
A		~a + b	B	C		AB = (~a + ~a) (ñì. ðèñ. 101).
A		~a + b	B	C		При < 0 оба вектора ме-
		~	~			При < 0 оба вектора ме-
		~	~			няют направления на противо-
	(~a + b) = ~a + b					няют направления на противо-
		Ðèñ. 101				положные.

~~ ~

6.1) F4; 2) F10; 3) 0.

7.a = b.

		~	~			~	~
8.	~c	b	;	b+~c	~c	, b	+	b+~c	.
	c	b			c
				j~b+~cj		b		j~b+~cj

10. Векторы ~anj (j = 1; : : : ; m); проведенные последовательно от одной вершины многоугольника к другой, образуют замкнутый

многоугольник, поэтому	m	~anj	~
	j=1		= 0: Если все складываемые ком-

планарные векторы повернуть на один и тот же угол в плоскости, в которой они лежат, то их суммарный вектор, не меняя своей ве-

личины, повернется на тот же угол. В данном случае

j=1 aj ~enj

это тот же по длине вектор, что и

ернутый на 90

j=1 ~aj ; íî ïîâ

Следовательно,

= ~0:

j=1 aj ~enj

11.

= p~ + q;~

CD = q~

p;~ DE =

p;~ EF

q;~ F A = p~

~q; AC

p:~

AD = 2q;~ AE = 2q~

12.

p~ +

1 ~

AD = f + p;~ AC = AB + BC = p~ +

AD =

f ; EF =

2 (p~ + f ); !

AF =

(f p~):

14.~r = (m1~r1 + m2~r2 + m3~r3)=(m1 + m2 + m3):

15. По формуле (1.15), согласно условию задачи, находим:

~rM

1 (~rA + ~rB ); ~rN

= 1

(~rC + ~rD ); ~rP =

1 (~rB + ~rC );

~rQ =

1 (~rA + ~rD ); ~rK

= 1 (~rM + ~rN ) = 1 (~rA + ~rB + ~rC + ~rD ):

+ ~r

);

(~r

Следовательно,

P Q = ~rQ

~rP

P K =

4 (~r

+ ~r

): Видим, что

= 1

P Q = 2P K, то есть точки

P; K; Q лежат на одной прямой, причем точка K делит отрезок P Q пополам.

210			Ответы и решения
16. Тело движется с постоянным ускорением, поэтому
	~at2
~vB = ~vA +~at; ~r = ~vA t+	2 : ( )
Из первого уравнения получим			D	C
~at2=2 = (~vB ~vA )t=2.			~vA	C
~at2=2 = (~vB ~vA )t=2.		A	~vA
Следовательно, вектор	переме-		~r
щения можно записать в виде		~a
		~a	B
~r = (~vA + ~vB )t=2:	( )		B	~vB
~r = (~vA + ~vB )t=2:	( )		Ðèñ. 102	~vB
			Ðèñ. 102

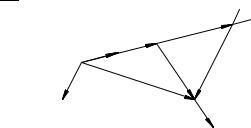
Из точки A проведем прямую вдоль вектора ~vA , а из точки B прямую параллельную вектору ускорения ~a. Эти прямые пересекут-

ся в точке	C. Соединим точки			AB	= ~r: Согласно
			A и B, получим !
уравнению (			AC = ~vA t è CB = ~at2=2:
		) и выполненным построениям, !			!
			AD =		1 AC = ~vA t=2:
Разделим отрезок AC пополам, получим !					2 !
Очевидно, что ! ! !				!	! !
~r ~vA t=2:		AB = AD + DB. Таким образом,		DB = AB + AD =
	Подставляя сюда радиус-вектор ~r из формулы ( ), на-
ходим !					!
DB	= ~vB t=2: Значит скорость ~vB направлена вдоль DB, и

vB =vA = DB=AD. Измеряя с помощью миллиметровой линейки длины отрезков DB и AD, находим vB =vA = 0:86.

18.1 = 1, 2 = 2, 3 = 3, 4 = 4:

19.Размерность пространства n; базисом такого пространства

является, например, система степеней t0; t, t2, : : :, tn 1:

20. 1) p1 = q1; p2 = q2; p3 = q3; 2) из условия коллинеарности

векторов p~ = ~q следует, что p1	= p2	= p3	:
q1	q2	q3

21. 1) Возможны четыре вектора, из которых никакие два не являются коллинеарными и никакие три компланарными; если два из четырех векторов коллинеарны, то все четыре компланарны; если три вектора коллинеарны, то коллинеарны все четыре; если три

вектора компланарны, то компланарны все четыре. 2) b; ~c; d компла-

нарны. 3) ~c и d коллинеарны. 4) d = 0:

22.

~ ~

3A +22B 3

3C + 4D = 0:

23.

A =

5 B +

5 C +

5 D:

коллинеарен

24. 1) = = 0, åñëè ~c = 0; 2) = 0 è 6= 0, åñëè ~c

b; 3) = 0 и 6= 0, если ~c коллинеарен вектору ~a.

28. v =

cos(~v; ~e1) =

17;

cos(~v; ~e1) = 2= 17;

cos(~v; ~e2) = 2= 17;

3=p

29.x = 1; y = 0; z = 1 (см. формулу (1.22)).

30.(AB)x = 4; (AB)y = 1:

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2021 / 2221 22 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.03.2016149.5 Кб11Б3.Б.4.4 ИЗЛ 1-й пол 19 в..doc
#
08.11.2018817.66 Кб31Банковское Дело - курс лекций.doc
#
03.05.2019729.6 Кб12Банковское дело ЛЕКЦИИ.doc
#
18.11.20183.4 Mб10Барулин В.С. - СОЦИАЛЬНАЯ ФИЛОСОФИЯ.doc
#
04.11.2018187.9 Кб12баскетбол ФГОС.doc
#
29.03.20161.13 Mб401Беляев Ю.Н. Введение в векторный анализ.pdf
#
16.11.20191.43 Mб14Беляева Теория вероятностей методичка 2006.doc
#
28.03.2016746.5 Кб26БЖД.doc
#
30.07.2019119.3 Кб1БЖД.doc
#
15.07.20193.68 Mб5Библер В.С. - ОТ НАУКОУЧЕНИЯ - К ЛОГИКЕ КУЛЬТУР....rtf
#
28.03.20169.12 Mб21Бизнес план.doc