
Беляев Ю.Н. Введение в векторный анализ
.pdf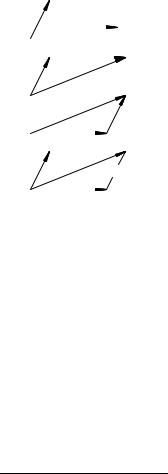
Ÿ 1. Геометрическое понятие вектора |
11 |
ãäå ~ea единичный вектор, совпадающий по направлению с данным вектором ~a и имеющий модуль, равный единице j~eaj= 1:
|
1.6. |
Сложение векторов. |
Ï ð à â è ë î |
ò ð å ó ã î ë ü í è- |
||||||||||||
к а: сумма двух векторов ~a |
~ |
|
|
|
||||||||||||
и b (рис. 4a) одинаковой физической |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
размерности это вектор ~c = ~a + b; определяемый по правилу |
||||||||||||||||
a) |
~a |
~ |
|
|
|
|
|
треугольника (рис. 4b), т.е. вектор, |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
b |
|
|
|
|
|
идущий из начала вектора ~a в конец |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
~ |
|
|
|
|
|
|
~ |
|
|
|
||
|
|
|
|
|
|
|
|
|
вектора b, если последний параллель- |
|||||||
|
|
|
|
|
|
b |
|
|
|
|
|
ным переносом совмещен своим нача- |
||||
b) |
~a |
|
|
|
~ |
|||||||||||
|
|
|
лом с концом вектора |
~a. |
||||||||||||
|
|
|
|
|
|
|
~a + b |
|||||||||
|
~ |
|
|
|
|
|
|
|
|
|
Аналогичный результат для сум- |
|||||
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|||
|
|
b + ~a |
|
|
|
|
|
|
получается при построении |
|||||||
c) |
|
|
|
~ |
|
|
~a |
ìû ~a + b |
||||||||
|
|
|
|
|
|
b |
|
|
|
|
|
ïî ï ð à â è ë ó ï à ð à ë ë å ë î ã ð à ì ì à |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 4d): если параллельным перено- |
||||
d) |
~a |
|
|
|
~ |
|||||||||||
|
|
|
сом совместить начала векторов ~a и |
|||||||||||||
|
|
|
|
|
|
|
~a + b |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b, |
то сумма ~a + b это вектор, про- |
|||
|
|
|
|
~ |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
веденный из общего начала векторов ~a |
|||||||
|
|
|
|
|
|
b |
|
|
|
|
|
|||||
|
|
|
|
Ðèñ. 4 |
|
|
|
|
|
~ |
|
|
|
|||
|
|
|
|
|
|
|
|
|
и b по диагонали параллелограмма, по- |
|||||||
строенного на векторах ~a |
~ |
|
2 |
. |
||||||||||||
и b как на сторонах |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
По определению векторной суммы, если векторы ~a и b не |
|||||||||||||||
коллинеарны, то вектор |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
(1.3) |
|
|
|
|
|
|
|
|
|
|
|
|
~c = ~a + b |
|
|||
при любых числах и параллелен плоскости, определяемой
~
векторами ~a и b. Другими словами, равенство (1.3) есть усло-
~
вие того, что три вектора ~a; b и ~c параллельны одной плоскости. Такие векторы называют компланарными3.
1.7. Основные свойства векторов. Сложение по правилу треугольника (параллелограмма) и умножение на числа
2Правило сложения векторов, наглядно представленное на рис. 4, было
впервые сформулировано голландским математиком и физиком С. Стевином (Simon Stevin, 1548-1620) в 1586г. в работе ½Начала статики\.
3Данный термин, образованный из латинского слова planus плоский и приставки co (con, cum), означающей совместность, в современное век-
торное исчисление ввел Гиббс (1901).

12 |
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
по правилу (1.1) это именно те условия, которые делают направленный отрезок вектором, т.е. являются определяющими условиями вектора.
К основным свойствам операции сложения векторов, вытекающим из е¼ определения, относятся следующие.
Сложение векторов коммутативно4, то есть cумма не зависит от перемены мест слагаемых векторов (сравни рис. 4b и 4c):
~ ~ |
(1.4) |
~a + b = b + ~a: |
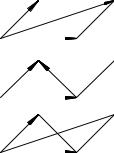
Сложение векторов ассоциативно5, а именно, для любых
~ |
и ~c (рис.5) выполняется равенство |
|
|
||||
векторов ~a, b |
|
|
|||||
~ |
|
~ |
~ |
(1.5) |
|||
|
b |
|
|
(~a + b) + ~c = ~a + (b + ~c): |
|||
|
~a |
~ |
~c |
|
|
||
|
Свойство (1.5) иначе называет- |
||||||
|
|
b + ~c |
|
ся законом сочетательности. |
|||
~ |
|
|
|||||
|
~a + b |
|
|
Умножение вектора на чис- |
|||
|
|
|
|
||||
~ |
~ |
|
|||||
ло обладает свойством ассоци- |
|||||||
|
~a + (b + ~c) = (~a + b) + ~c |
||||||
Ðèñ. 5 |
ативности |
|
|
||||
|
|
( ~a) = ( )~a = ( ~a): |
|
(1.6) |
|||
Докажем первое из равенств формулы (1.6) (при этом второе автоматически следует из коммутативности умножения чи- сел = ).
Модули векторов ( ~a) и ( )~a одинаковы и равны j jj jj~aj. Если числа и одного знака, то векторы ( ~a) и ( )~a направлены в ту же сторону, что и ~a. В противном случае векторы также направлены одинаково (противоположно ~a). Наконец, ес-
~
ли одно из чисел или равно нулю, то ( ~a) = ( )~a = 0. Таким образом, равенство ( ~a) = ( )~a выполняется при любых и .
Умножение вектора на число обладает двумя свойствами
4От латинского commutare менять, переменять.
5От латинского associare присоединять.

Ÿ 1. Геометрическое понятие вектора |
|
13 |
дистрибутивности6, или распределительности, |
|
|
( + )~a = ~a + ~a; |
(1.7) |
|
~ |
~ |
(1.8) |
(~a + b) = ~a + b: |
||
Докажем свойство (1.7). Оно очевидно, если хотя бы одно из чисел , или вектор ~a равны нулю. Поэтому будем считать, что , , ~a отличны от нуля.
Если числа > 0 и > 0, то векторы ~a и ~a одинаково направлены, и абсолютная величина вектора ~a + ~a равнаj~aj + j~aj = ( + )j~aj: Абсолютная величина вектора ( + )~a также равна ( + )j~aj: Значит, равенство (1.7) для данного слу- чая доказано.
При < 0 и < 0 векторы ~a и ~a, как и в предыдущем случае, одинаково направлены, и абсолютная величина вектора
~a+ ~a равна j ~aj+j ~aj = j~aj j~aj = ( + )j~aj: Абсолютная величина ( + )~a равна j + jj~aj = ( + )j~aj: Таким образом, равенство (1.7) выполняется и в этом случае.
Наконец, рассмотрим случай, когда числа и имеют разные знаки. Для определенности будем считать > 0 и < 0. Векторы ( + )~a и ~a + ~a, стоящие в левой и правой частях формулы (1.7), будут направлены одинаково в направлении ~a, если > j j, и противоположно ~a, если < j j. Абсолютная величина вектора ~a + ~a равна jj ~aj j ~ajj = j j~aj j jj~ajj = j( j j)j~ajj: И абсолютная величина ( + )~a равна j( j j)j~ajj. Свойство (1.7) доказано.
Формулы (1.5) - (1.8), очевидно, справедливы и для большего числа векторов и скалярных множителей.
1.8. Правило многоугольника. Сумма ~sn нескольких векторов ~a1; ~a2; ~a3; : : : ; ~an (см. рис. 6a), согласно правилу треугольника и свойству (1.5), может быть найдена согласно рекуррентной формуле:
~sn = ~a1 + ~a2 + ::: + ~an = = ~sn 1 + ~an;
6От английского distributive распределительный.

14 |
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
|
||||||
ãäå ~sn 1 сумма первых (n 1) векторов. |
|
|
||||||
Это эквивалентно следующему геометрическому |
построе- |
|||||||
|
|
|
|
|
|
|
! |
, |
нию. Из произвольной точки O (рис. 6b) проводим вектор OA1 |
||||||||
|
1 |
, затем из точки A |
1 |
|
|
! |
, |
|
равный вектору ~a |
|
|
проводим вектор A1A2 |
|||||
2 |
|
|
|
|
|
! |
: |
|
равный ~a |
: По правилу треугольника находим вектор OA2 = ~s2 |
|||||||
Далее из точки A |
2 |
! |
, равный ~a3 |
; è íàõî- |
||||
|
проводим вектор A2A3 |
|||||||
äèì ~s3 = ~s2 + ~a3. Продолжая таким образом, находим точку Anконец вектора, равного вектору ~an (ðèñ. 6b).
~a1 |
|
A3 |
A2 |
|
|
|
~an |
|
|
|
|
||
|
|
|
|
|
|
|
An |
~s3 ~s2 |
|
|
|
|
|
~a2 |
~sn |
|
A1 |
|
|
|
~a3 |
|
|
|
|
|
|
|
|
|
~c ~a |
|
~c |
|
a) |
O |
b) |
~ |
~ |
||
|
b |
b |
||||
|
Ðèñ. 6 |
|
Ðèñ. 7 |
|
|
|
Вектор OAn представляет собой сумму векторов |
|
|
||||
! |
|
|
|
|
|
|
~s = ~a1 + ~a2 + ::: + ~an;
и замыкает многоугольник, сторонами которого являются скла-
дываемые векторы ~a1; ~a2; ~a3; : : : ; ~an: |
|
|
|||
1.9. |
Разность векторов |
~ |
|
|
|
~a и b это такой вектор ~c, ко- |
|||||
|
|
|
~ |
|
|
торый при сложении с вектором b дает вектор ~a (рис. 7). Иначе |
|||||
говоря, |
~ |
|
|
~ |
~ |
~c = ~a b это сумма векторов ~a и |
b; ãäå |
b вектор |
|||
|
~ |
|
~ |
|
|
противоположный b (он получается из b умножением на -1). |
|||||
П р и м е р 1. Выясним, какие ограничения накладывают |
|||||
|
~ |
|
|
|
|
на векторы ~a и b следующие соотношения: |
|
|
|||
|
~ |
~ |
~ |
~ |
|
|
1) j~a + bj = j~a bj; 3) j~a + bj = j~aj + jbj; |
||||
|
~ |
~ |
~ |
~ |
|
|
2) ~a + b = "(~a b); 4) j~a bj = j~aj jbj: |
||||
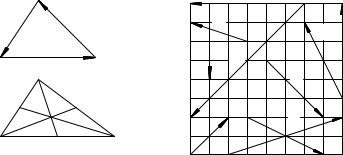
Геометрический смысл суммы и разности двух векторов ~a и
~ |
|
b это векторы, направленные по диагоналям параллелограм- |
|
ма, построенного на векторах ~a и |
~ |
b, как на сторонах. Сумма |
|
~ |
~ |
~a + b направлена по диагонали из общего начала векторов ~a и b
~
(см. рис. 8a), а разность ~a b по второй диагонали (см. рис. 8b).
Ÿ 1. |
Геометрическое понятие вектора |
|
|
|
|
|
|
|
|
|
|
|
15 |
||||||||||||
|
Первое из рассматриваемых соотношений означает, что ди- |
||||||||||||||||||||||||
агонали |
имеют |
одинаковую длину. Значит, параллелограмм |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
взаимно перпен- |
||||||||||
является прямоугольником, т.е. векторы ~a и b |
|||||||||||||||||||||||||
дикулярны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из второго равенства следует колли- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|||
неарность векторов ~a и b. Только в этом |
a) |
~a |
|
|
|
|
|
|
|
|
|||||||||||||||
случае диагонали параллелограмма па- |
|
~a + b |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
~ |
|
|
|
|
|
|
|
|
||||||||||||||
раллельны друг другу. |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Длина одной из сторон треугольника |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|||||||||||||
равна сумме длин двух других сторон b) |
~a |
|
~ |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
~a b |
|
|
|
||||||||||||||||||||
вот смысл третьего соотношения. Это |
|
|
|
b |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
B |
|
|
|
|
|
|
|
C |
||||||||||||||
возможно лишь при одинаковой направ- |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
M |
|
|
|
|
|
|
|||||||||||||||
ленности векторов |
~ |
|
|
|
|
|
c) |
~a |
|
|
|
|
|
|
|
|
|||||||||
~a è b. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Наконец, в четвертом случае векто- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
A |
|
|
~ |
|
|
|
D |
|
|
|
|||||||||||||||
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ðû |
~a |
|
направлены в противополож- |
|
|
b |
|
|
|
|
|
||||||||||||||
è |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ные стороны. |
|
|
|
|
|
|
|
|
|
|
Ðèñ. 8 |
|
|
|
|
|
|
||||||||
|
П р и м е р 2. В параллелограмме ABCD (смотри рис. 8c) |
||||||||||||||||||||||||
обозначены: ! |
|
! |
|
~ |
|
|
точка пересечения диагона- |
||||||||||||||||||
|
|
|
|
|
AB = ~a; AD = b è M |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
~ |
векторы |
! ! |
||||||||||||
лей параллелограмма. Выразим через ~a и b |
|||||||||||||||||||||||||
! ! |
|
|
|
|
|
|
|
|
|
|
|
|
|
M A; M B; |
|||||||||||
M C; M D: |
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По правилу сложения векторов |
AC = ~a+b, и, следовательно, |
|||||||||||||||||||||||
|
! |
! |
2 |
! |
|
|
2 |
|
|
|
|
||||||||||||||
! |
|
2 |
! |
2 |
~ |
|
|
|
|
|
|
|
|
~ |
|||||||||||
M A = |
|
1 |
AC = |
1 |
|
Аналогично M B = |
1 |
DB = |
1 |
|
|
||||||||||||||
|
|
|
(~a + b): |
|
|
|
(~a b): |
||||||||||||||||||
Наконец, ! |
! |
2 |
~ |
|
|
! |
! |
2 |
|
~ |
|
|
|
|
|||||||||||
|
|
|
|
|
M C = M A = |
1 |
|
è M D = M B = |
1 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
(~a + b); |
|
(b ~a): |
|||||||||||||||||
Задачи
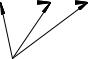
1. |
~ |
Какому условию должны удовлетворять три вектора ~a, b, |
~c, чтобы из них можно было образовать треугольник? Указание: см. рис. 9.
2. Доказать неравенство |
|
|
~ |
~ |
(1.9) |
j~a + bj j~aj + jbj: |
||
Какой геометрический смысл оно имеет?
3.Доказать свойство (1.8).
4.Доказать, что можно построить треугольник, стороны которого равны и параллельны медианам данного ABC
(ðèñ.10).
! ! ! ~
Указание. Показать, что из условия AB + BC + CA = 0 следует
!0 !0 !0 ~
равенство AA + BB + CC = 0.
16 |
|
|
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
||||||||||||
5. Пусть A0; B0; C0 |
середины сторон ABC; а O произ- |
||||||||||||||
вольная точка. Доказать равенство |
!0 |
|
|
!0 |
!0 |
= |
OA + |
||||||||
OA |
+ OB |
+ OC |
! |
||||||||||||
OB + OC: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
! |
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. На плоскости заданы векторы |
~ |
~ |
|
~ |
|
|
|
|
|||||||
F1; F2 |
,...,F10 (ðèñ.11). Íàé- |
||||||||||||||
òè: 1) |
~ |
~ |
~ |
|
~ |
~ |
~ |
~ |
|
|
|
~ |
: |
|
|
F1 |
+ F2 |
+ F3 |
; 2)F6 F1 |
; 3)F1 + F2 |
+ : : : + F10 |
|
|
||||||||
|
|
|
|
|
|
|
|
~ |
|
|
C |
|
|
||
|
|
|
|
|
|
|
|
F4 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
~ |
|
L |
|
|
|
~ |
|
|
~c |
|
|
|
|
|
|
|
|
|
|
F2 |
||
Ðèñ. 9 |
|
|
b |
|
|
|
F7 |
|
|
|
|
~ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
F10 |
|||
|
|
|
~a |
|
|
|
B |
|
|
~ |
|
K |
|
||
|
|
|
|
|
|
|
|
|
|
|
F3 |
|
|
|
|
|
|
|
B |
|
|
|
|
~ |
|
|
|
O |
~ |
|
|
|
|
|
|
|
|
|
F8 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
F5 |
|
|
|
|
|
C0 |
|
|
A0 |
|
Ðèñ. 11 |
|
|
|
A |
|
|
G |
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
F1 |
|
|
|
|
|
|
Ðèñ. 10 |
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F9 |
|
~N |
||
|
A |
B |
0 |
C |
|
|
D |
E |
|
||||||
|
|
|
|
|
|
|
|
|
F6 |
||||||
7. Какому условию должны удовлетворять векторы |
~ |
||||||||||||||
~a è b, |
|||||||||||||||
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
чтобы угол между векторами ~a + b и ~a был в два раза меньше, |
|||||||||||||||
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
чем между ~a и b? |
|
AB = ~c и BC = ~a; служащие сторонами |
|||||||||||||
8. |
|
|
|
|
|||||||||||
|
Зная векторы ! |
! |
|
|
|
|
|
|
|
|
|||||
треугольника ABC, найти векторы, коллинеарные биссектри- |
|||||||||||||||
сам углов этого треугольника.
|
|
|
|
|
|
~ |
|
9. Из трех произвольных векторов ~a; b и ~c образованы век- |
|||||||
òîðû |
~ |
~ |
~ |
|
~ |
~ |
|
A |
= ~c b; |
B = ~a ~c; |
C |
= b ~a: Доказать |
|||
|
|
|
~ ~ |
~ |
при любых не равных нулю |
||
компланарность векторов A; B и C |
|||||||
числах ; ; . |
|
|
|
|
|
||
Указание. Найти такие числа "1 |
è "2, с помощью которых один из |
||||||
|
|
~ |
|
|
|
~ |
~ |
векторов, например A, можно выразить через два других B |
è C: |
||||||
~ |
~ |
~ |
|
|
|
|
|
A = "1B + "2C (смотри условие компланарности трех векторов (1.3)).
10. Дан плоский m-угольник, длины сторон которого есть aj (j = 1; : : : ; m). Обозначим единичные векторы, перпендикулярные к сторонам aj и все направленные во внутреннюю
область многоугольника (или все во внешнюю область) через
~enj (j = 1; : : : ; m). Найти Pm aj~enj :
j=1
11. В правильном шестиугольнике ABCDEF известны
! ! ! !
AB = p~ и BC = q:~ Выразить через p~ и q~ векторы: CD; DE;
! ! ! ! !
EF ; F A; AC; AD è AE:

Ÿ 2. |
Примеры векторов |
|
17 |
|
! |
12. В правильном шестиугольнике ABCDEF известны |
|||
! |
~ |
~ |
! ! |
|
AB = p~ и AE = f : Выразить через p~ и f |
векторы: AC; AD; |
|||
! ! |
|
|
|
|
AF ; EF : |
|
|
|
|
Ÿ 2. Примеры векторов
2.1.Радиус-вектор точки. Если за начало отсчета вы-
брать точку O, то положение любой другой точки M отно-
!
сительно O определяется вектором OM , который называется
радиусом-вектором точки M и обозначается ~r. Про точку M , заданную радиус-вектором ~r, говорят, для сокращения речи, что дана точка M (~r). Рассмотрим несколько примеров.
Ï ð è ì å ð 3. Ó ð à â í å í è å ï ð ÿ ì î é, ï ð î õ î ä ÿ ù å é ÷ å-
ð å ç ò î ÷ ê ó A(~a), ï à ð à ë ë å ë ü í î |
~ |
â å ê ò î ð ó b, åñòü |
|
~ |
(1.10) |
~r = ~a + b; |
где ~a определяет точку A(~a), через которую проходит прямая, а переменный параметр.
|
|
|
|
|
|
Справедливость формулы (1.10) пока- |
|
|
|
|
|
|
жем с помощью следующих построений. |
|
|
~ |
|
|
~ |
|
|
|
|
M |
Отложим из точки O векторы b и ~a. Через |
||
|
|
A b |
|
точку A проведем прямую параллельно |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
~a |
|
~r |
|
|
вектору b, как это показано на рис.12. По- |
|
|
|
|
ложение произвольной точки M , принад- |
||
|
|
|
|
|
||
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
O |
|
|
|
b |
|
лежащей данной прямой, зададим радиус- |
|
|
|
|
|
||
Ðèñ. 12 |
вектором ~r. |
|
|
|
|
Вектор ! |
|
|
|
||
|
|
|
|
~ |
|
AM по построению коллинеарен вектору b, следова- |
|||||
|
|
|
|
|
~ |
тельно, его можно представить в виде произведения b и подхо- |
|||||
|
|
|
|
|
~ |
|
|
|
|
AM = b. Согласно пра- |
|
дящим образом выбранного числа : ! |
|
||||
|
|
|
|
~ |
|
вилу треугольника имеем |
AM = ~r ~a = b; что и дает искомое |
||||
! |
|
|
|
||
|
|
|
|
|
|
векторное уравнение прямой.
П р и м е р 4. У р а в н е н и е п р я м о й, п р о х о д я щ е й ч е- р е з д в е з а д а н н ы е т о ч к и. Составим векторное уравнение прямой линии, проходящей через точки M1(~r1) è M2(~r2). Возьмем на этой прямой произвольную точку M (~r) (см. рис. 13). Необходимым условием того, что три точки M1(~r1); M2(~r2)
18 |
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
и M (~r) лежат на одной прямой, является компланарность векторов ~r1; ~r2 и ~r; определяющих эти точки. Это условие можно записать в форме, подобной равенству (1.3):
M1 |
|
M2 M |
~r = ~r1 + ~r2: |
(1.11) |
||
~r1 |
~r2 |
~r |
Выясним, какими должны быть числа |
|||
и , чтобы три точки M1(~r1); M2(~r2) è M (~r), |
||||||
|
|
|
|
|||
|
O |
|
|
связанные равенством (1.11), лежали на од- |
||
|
Ðèñ. 13 |
ной прямой. |
|
|||
Очевидно, что если бы векторы ~r1 è ~r2 были коллинеарны, то точка M (~r); определяемая вектором ~r из равенства (1.11), лежала бы на одной прямой с точками M1(~r1) è M2(~r2) ïðè
любых и . |
|
|
|
|
|
|
Рассмотрим теперь более общий случай, когда векторы ~r1 è |
||||
~r2 |
не коллинеарны, как это и изображено на рис.13. |
||||
|
! |
|
! |
|
~r1 лежат на одной |
|
Векторы M1M2 = ~r2 |
|
~r1 è M1M = ~r |
|
|
прямой. Следовательно, |
|
|
|||
|
|
|
|
||
|
~r ~r1 = (~r2 ~r1): |
|
(1.12) |
||
Разрешим это уравнение относительно вектора ~r:
~r = (1 )~r1 + ~r2: |
(1:100) |
Сравнивая полученное равенство с формулой (1.11), находим
+ = 1: |
(1.13) |
Таким образом, формула (1.11) при условии (1.13) это векторное уравнение прямой, проходящей через две точки M1(~r1)
è M2(~r2). Если коэффициент > 1, или < 0, то точка M (~r); согласно равенству (1.12), находится вне отрезка M1M2. При 0 1 радиус-вектор ~r определяет точку M; лежащую на прямой между точками M1 è M2:
П р и м е р 5. Р а д и у с-в е к т о р т о ч к и, д е л я щ е й о т- р е з о к в з а д а н н о м о т н о ш е н и и. Пусть M (~r) точ- ка, делящая отрезок M1M2 (рис.14) в заданном отношении M1M=M M2 = = . Выразим радиус-вектор ~r точки M через радиус-векторы ~r1 è ~r2 точек M1 è M2.

Ÿ 2. Примеры векторов |
|
|
|
|
|
19 |
||||
Очевидно, что длину отрезка M1M2 можно представить в |
||||||||||
1 |
|
2 |
1 |
|
2 |
|
|
|
1 |
! |
âèäå M |
M |
|
= M |
M + M M |
|
= |
1 + |
|
M |
M: Векторы M1M è |
! |
направлены в одну сторону, поэтому данное равенство |
|||||||||
M1M2 |
||||||||||
|
|
|
|
|
|
! |
! |
èëè ( + |
||
можно заменить на векторное: ( + )M1 M = M1M2 |
||||||||||
)(~r ~r1) = (~r2 ~r1): |
|
|
|
|||||||
|
|
|
|
Разрешая последнее уравнение относи- |
||||||
|
|
|
|
тельно ~r; находим |
|
|
|
|||
M1 |
M M2 |
|
|
~r = |
~r1 + ~r2 |
: |
(1.14) |
|||
|
||||||||||
|
|
|
|
|
|
|
+ |
|
|
|
~r1 ~r |
~r2 |
В частности, радиус-вектор середины от- |
||||||||
|
|
|
|
|||||||
|
O Ðèñ. 14 |
резка ( = = 1=2) выражается форму- |
||||||||
|
ëîé |
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
(1.15) |
|
|
|
|
|
~r = |
|
(~r1 + ~r2): |
|
|
||
|
|
|
|
2 |
|
|
||||
П р и м е р 6. Т о ч к а п е р е с е ч е н и я м е д и а н т р е у- г о л ь н и к а. Докажем, что медианы треугольника пересекаются в одной точке, и найдем радиус-вектор точки пересечения.
|
|
|
|
Пусть вершины A, B и C ABC опре- |
||||
|
B |
|
|
деляются векторами ~rA; ~rB ; ~rC : Обозначим |
||||
|
C0 |
|
A0 |
середины сторон ABC, противолежащих |
||||
|
|
вершинам A; B и C; соответственно буква- |
||||||
|
|
|
|
|||||
|
|
|
|
ìè A0; B0 è C0 (ðèñ.15). |
|
|
||
A |
B0 |
C Выпишем радиус-векторы этих точек в |
||||||
Ðèñ. 15 |
соответствии с формулой (1.15): |
|
||||||
A0: ~rA0 = |
1 |
(~rB + ~rC ); B0: ~rB0 = |
1 |
(~rA + ~rC ); C0: ~rC0 = |
1 |
(~rA + ~rB ): |
||
2 |
|
2 |
||||||
|
|
|
2 |
|
|
|||
По формуле (1:100) составим уравнения медиан:
AA0 : ~r = (1 )~rA + ~rA0 = (1 )~rA + 2 (~rB + ~rC );
CC0 : ~r = (1 )~rC + ~rC0 = (1 )~rC + 2 (~rA + ~rB ):
Оба эти выражения должны давать один и тот же радиусвектор для точки пересечения медиан AA0 è CC0: Поэтому

20 |
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
для нахождения этого радиус-вектора приравняем правые ча- сти двух последних формул. Имеем
(1 )~rA + |
|
(~rB + ~rC ) = (1 )~rC + |
|
(~rA + ~rB ): |
|
|
|||
2 |
2 |
Объединим здесь слагаемые, содержащие одинаковые радиусвекторы
1 2 |
~rA + |
|
2 |
2 |
~rB + |
|
2 |
1 + ~rC = ~0: (1.16) |
||
|
|
|
|
|
|
|
|
|
|
|
Равенство (1.16) выполняется, если коэффициенты при ~rA; ~rB ; ~rC равны нулю. Следовательно,
= = 23 ;
точка пересечения медиан AA0 è CC0 имеет следующий радиусвектор
r = |
1 |
(~rA + ~rB + ~rC ): |
(1.17) |
3 |
Выражение (1.17) симметрично по отношению к векторам ~rA; ~rB ; ~rC . И если бы мы определяли точку пересечения медиан BB0 è CC0, то получили бы тот же результат. Так что все три медианы пересекаются в одной точке, определяемой радиусвектором (1.17).
Из формул (1.14) и (1.17) нетрудно заметить, что точка пересечения делит каждую медиану в отношении 2 : 1 от вершины треугольника.
П р и м е р 7. Т о ч к а п е р е с е ч е н и я б и с с е к т р и с т р е- у г о л ь н и к а. Докажем, что биссектрисы ABC пересекаются в одной точке, и найдем радиус-вектор точки их пересечения.
Пусть вершины A, B и C определяются радиус-векторами ~rA; ~rB è ~rC соответственно, а длины противолежащих сторон
~
a, b и c. Векторы ~a, b и ~c удовлетворяют очевидным равенствам
~
(ñì. ðèñ. 16): ~a = ~rB ~rC ; b = ~rC ~rA; ~c = ~rA ~rB :
~
Из вершины A отложим единичные векторы ~eb = bb è ~ec =~cc : На этих векторах, как на сторонах строим ромб, диагональ
