
Беляев Ю.Н. Введение в векторный анализ
.pdf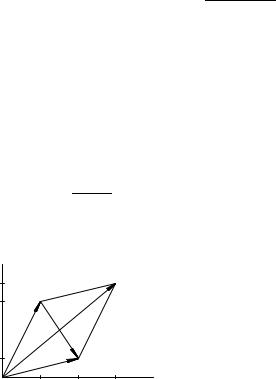
Ÿ 3. Линейное пространство |
|
31 |
Таким образом, |
|
|
z 1 z 2 = (a; b) = (a1 a2; b1 b2): |
(3 ) |
|
Частным от деления двух |
чисел z 1 = (a1; b1) è |
z 2 = |
(a2; b2) 6= 0 должно быть такое z = (a; b), что |
|
|
z 2z = z 1; òî åñòü |
(a2; b2)(a; b) = (a1; b1): |
|
Отсюда ввиду определения (2 ) получаем систему двух уравнений:
a2a b2b = a1; |
a2b + b2a = b1; |
|
|
|
|
|||
разрешая которую относительно a и b, находим |
|
|
|
|
||||
a = |
a1a2 + b1b2 |
; |
b = |
a2b1 a1b2 |
: |
(4 |
|
) |
|
||||||||
|
a22 + b22 |
|
a22 + b22 |
|
|
|
||
Множество комплексных чисел является обобщением множества действительных чисел. Действительно, точки (a; 0), принадлежащие оси абсцисс на плоскости комплексного переменного, взаимно однозначно соответствуют множеству действительных чисел, и применение к ним правил (1 ); (2 ); (3 ) и (4 ) дает формулы
(a1; 0) (a2; 0) = (a1 a2; 0); (a1; 0)(a2 ; 0) = (a1a2; 0);
(a1; 0) |
= (a1=a2; 0); a2 6= 0; |
(a2; 0) |
подтверждающие алгебраические свойства действительных чи- сел. Поэтому справедливо равенство
|
|
Im z |
|
|
b1 |
+ b2 |
z 1 |
|
z 1 + z 2 |
|
b1 |
|
|
|
|
|
|
|
|
|
b2 |
|
z 2 |
Re z |
|
0 |
|
|
|
|
a1 |
a2 |
a1 + a2 |
|
|
|
|||
|
|
Ðèñ. 22 |
|
|
(a; 0) = a; |
(5 ) |
и первое из пары действительных чисел, характеризующих комплексное число z = (a; b), называют действительной ча- стью комплексного числа и обозначают a = Re z11. Поэтому ось абсцисс действительная ось.

32 |
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
Рассмотрим точку (0,1), лежащую на расстоянии 1 от нача- ла координат вверх по оси ординат. Для этой точки придумано специальное обозначение с помощью буквы i: (0; 1) i. Применяя правило (2), находим
i2 = (0; 1)(0; 1) = ( 1; 0) = 1:
Число i (0; 1) называется мнимой единицей. Любая другая точка (0; b), лежащая на оси ординат плоскости комплексного переменного, соответствует произведению действительного числа b на мнимую единицу
(0; b) = (b; 0)(0; 1) = bi: |
(6 ) |
Второе из пары действительных чисел, характеризующих комплексное число z = (a; b), есть мнимая часть комплексного числа. Обозначается это так: b = Im z 12. Соответственно, ось ординат мнимая ось плоскости комплексного переменного.
Множество комплексных чисел C удовлетворяет всем свойствам (1.29)-(1.36) линейного пространства. Нулевым элементом здесь является комплексное число (0; 0).
Произвольное комплексное число z = (a; b) ввиду равенств (5 ) и (6 ) может быть представлено в виде
z = (a; b) = (a; 0) + (0; b) = a + ib = Re z + i Im z :
Комплексное число z = a + ib может изображаться радиусвектором точки z с проекциями a и b на координатные оси. Из рис. 22 ясен геометрический смысл операций сложения и вычитания комплексных чисел: сумма и разность комплексных чисел z 1 è z 2 изображаются соответственно векторами, равными направленным диагоналям параллелограмма, построенного на векторах z 1 è z 2.
Ï ð è ì å ð 12. Ì à ò ð è ö û.
Рассмотрим множество прямоугольных матриц одной размерности.
12 Обозначение Im происходит от первых двух букв слова imaginary воображаемый, мнимый.
Ÿ 3. Линейное пространство |
33 |
Матрицей M из n строк и k столбцов (матрица размерности n k) называется таблица из n k чисел mij (i = 1; 2; : : : ; n; j = 1; 2; : : : ; k); заключенная в круглые скобки:
|
0 m21 |
m22 |
: : : m2k 1 |
|
|
||
|
|
m11 |
m12 |
: : : m1k |
C |
|
|
|
B .. .. |
. . . .. |
|
|
|||
M = |
B |
. . |
. |
C |
: |
(1.37) |
|
|
B mn1 |
mn2 |
: : : mnk C |
|
|
||
|
@ |
|
|
|
A |
|
|
Числа mij , входящие в состав матрицы, элементы мат-
ðèöû.
Суммой двух матриц U и V называется матрица W , каждый элемент которой wij равен арифметической сумме соответствующих элементов uij è vij складываемых матриц:
|
u11 |
u12 |
: : : u1k |
1 |
|
|
v11 |
v12 |
: : : v1k |
1 |
|
|
u21 |
u22 |
: : : u2k |
|
|
v21 |
v22 |
: : : v2k |
|
||
W = U + V |
0 . . |
. |
+ |
0 . . |
. |
= |
|||||
|
B .. .. |
. . . .. |
C |
|
B .. .. |
. . . .. |
C |
|
|||
|
@ |
|
|
A |
|
@ |
|
|
|
A |
|
|
B un1 |
un2 |
: : : unk C |
|
B vn1 |
vn2 |
: : : vnk C |
|
|||
0 |
. |
. |
|
u11 + v11 |
u12 + v12 |
= |
u21 + v21 |
u22 + v22 |
|
|
|
@ |
|
.. |
B .. |
||
B un1 + vn1 |
un2 + vn2 |
|
:: : u1k
:: : u2k
. . .
:: : unk
+ v1k |
1 0 |
w11 |
|
+ v |
|
w |
|
. |
2k |
.21 |
|
.. |
|
C B .. |
|
+ vnk |
C B wn1 |
||
|
|
A @ |
|
w12 |
: : : w1k |
1: |
w22 |
: : : w2k |
|
. |
. |
|
.. |
. . . .. |
C |
|
|
A |
wn2 |
: : : wnk C |
|
Произведением матрицы A с элементами aij на число
называется матрица с элементами aij (i = 1; 2; : : : ; n; j = 1; 2; : : : ; k):
|
|
a11 |
a12 |
: : : a1k |
1 |
|
|
a11 |
a12 |
: : : a1k |
1 |
|
|
|
a21 |
a22 |
: : : a2k |
|
|
a21 |
a22 |
: : : a2k |
|
||
A = A = |
0 . . |
. |
= |
0 . |
. |
. |
: |
|||||
|
B .. .. |
. . . .. |
C |
|
B .. |
.. |
. . . .. |
C |
|
|||
|
@ |
|
|
|
A |
|
@ |
|
|
|
A |
|
|
B an1 |
an2 |
: : : ank C |
|
B an1 |
an2 |
: : : ank C |
|
||||
Нулевым элементом множества является матрица, все элементы которой равны нулю.
П р и м е р 13. Множество всех многочленов относительно переменной вида
a = + ; |
(1.38) |
где и действительные числа.
34 |
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
Элементы a, определяемые формулой (1.38), образуют линейное пространство, в котором
a = + ; a 1 + a 2 = ( 1 + 2) + ( 1 + 2) ;
и нулевым элементом является 0 = 0 + 0 = 0:
3.2. Размерность и базис линейного пространства.
Линейная комбинация векторов a 1; a 2; :::; a n это сумма их произведений на некоторые числа 1; :::; n :
1a 1 + 2a2 + ::: + na n:
Векторы a 1; a 2; :::; a n линейно зависимы, если нулевой вектор можно представить в виде их линейной комбинации
1a 1 + 2a 2 + ::: + na n = 0; |
(1.39) |
âкоторой не все коэффициенты i (i = 1; :::; n) равны нулю.
Ïр и м е р 14. Необходимым и достаточным условием коллинеарности двух векторов ~c и ~a является их линейная зависимость.
Действительно, если ~c и ~a коллинеарны, то ~c = ~a; или ~c
~
~a = 0, что, согласно определению (1.39), как раз и означает линейную зависимость векторов ~a и ~c.
~
И наоборот, если ~c и ~a линейно зависимы, то 1~c + 2~a = 0, и хотя бы один из коэффициентов 1, 2 не равен нулю. Пусть1 =6 0, тогда из последнего уравнения можно выразить вектор ~c через ~a: ~c = ( 2= 1)~a это значит, что ~c и ~a коллинеарны.
П р и м е р 15. Необходимым и достаточным условием ком-
~
планарности тр¼х векторов ~a, b, ~c является их линейная зависимость (см. формулу (1.3)).
Если равенство (1.39) выполняется только при 1 = 2 =
::: = n = 0, то векторы a 1; a 2; :::; a n линейно независимы.
Пространство L называется конечномерным, а число n числом измерений этого пространства, если в L существует n линейно независимых векторов, тогда как любые n+1 векторов в L линейно зависимы.
Ÿ 3. Линейное пространство |
35 |
Система из n линейно независимых заданных в определенном порядке векторов в n-мерном пространстве L
b1; b2; :::; b n 2 L |
(1.40) |
называется базисом пространства L.
Всякий вектор a 2 L можно единственным образом представить в виде линейной комбинации базисных векторов b i
(i = 1; :::; n). Действительно, уравнение
0a + 1b1 + ::: + nbn = 0 |
(1.41) |
должно иметь нетривиальное решение (n + 1 вектор в n-мерном пространстве!).
В этом уравнении 0 6= 0, в противном случае мы получили бы нетривиальное решение уравнения
1b1 + ::: + nbn = 0;
вопреки предположению, что векторы b i (i = 1; :::; n) образуют базис. Так как 0 =6 0, уравнение (1.41) можно разрешить относительно a:
a = 1b1 + ::: + nbn; |
(1.42) |
ãäå i = i= 0 (i = 1; :::; n).
Числа 1; 2; : : : ; n, с помощью которых вектор a представляется в виде линейной комбинации (1.42), называются координатами вектора a в базисе (1.40).
Покажем теперь, что координаты вектора в данном базисе определяются однозначно. Предположим противное: пусть существует по крайней мере еще одно представление вектора a в
базисе (1.40) (с координатами 0 (i = 1; :::; n)): |
|
i |
|
a = 10 b1 + ::: + n0 bn: |
(1.43) |
Вычитая почленно (1.43) из (1.42), получим |
|
( 1 10 )b1 + ( 2 20 )b2 + ::: + ( n n0 )bn = 0; |
(1.44) |

36 |
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
откуда в силу линейной независимости векторов базиса следует
i = i0; i = 1; : : : ; n;
что и требовалось доказать.
П р и м е р 16. Рассмотрим размерности и базисы некоторых линейных пространств из примеров 10-13.
1)Множество действительных чисел R одномерное, в каче- стве базисного вектора может использоваться любое действительное число, не равное нулю.
2)Множество комплексных чисел C двухмерное, в качестве базисных векторов могут использоваться, например, два комплексных числа z 1 = (1; 0) è z 2 = (0; 1).
3)Множество квадратных матриц размерности 2 2 че- тырехмерное линейное пространство. Пример базиса этого про-
странства:
|
0 |
0 |
; |
|
0 |
0 |
|
; |
|
1 |
0 |
; |
|
0 |
1 |
: |
(1.45) |
|
1 |
0 |
|
|
0 |
1 |
|
|
|
0 |
0 |
|
|
0 |
0 |
|
|
4) Множество многочленов (1.38) двухмерное линейное пространство. В качестве линейно независимых многочленов (базиса) можно взять 1 и . Тогда координатами будут числа
è .
Если выбрать, например, базис (1 + ); (1 ), то
a = + = |
( + ) |
(1 + ) + |
( ) |
(1 |
|
): |
|
2 |
|||||||
|
|
2 |
|
|
Теперь координатами элемента a в новом базисе являются ( +
)=2 è ( )=2.
Задачи 17. Проверить выполнение свойств 1.29-1.36 для множества
комплексных чисел C. |
|
|
|
|
18. |
Найти координаты матрицы |
1 |
2 |
в базисе (1.45). |
3 |
4 |
|||
19. |
Определить размерность и дать пример базиса линей- |
|||
ного пространства множества многочленов 0 + 1t + : : : +n 1tn 1, где в качестве основных операций берутся обычное сложение многочленов и умножение многочлена на число.
Ÿ 4. |
Разложение вектора на составляющие |
37 |
|||
Ÿ 4. |
Разложение вектора на составляющие |
||||
При нахождении модуля и направления суммы векторов, |
|||||
особенно в случае большого числа слагаемых, удобным являет- |
|||||
ся так называемый аналитический способ, основанный на раз- |
|||||
ложении вектора на составляющие. |
|
||||
Разложение вектора на составляющие это действие, об- |
|||||
ратное геометрическому сложению и состоящее в том, что дан- |
|||||
ный вектор заменяют равной ему суммой нескольких векто- |
|||||
ров. Геометрически это сводится к построению ломаной линии, |
|||||
имеющей данный вектор замыкающей стороной. Число таких |
|||||
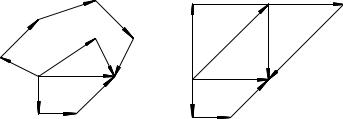
разложений бесконечно много. Так, в примере, показанном на |
|||||
рис. 23, представлено три из возможных разложений вектора ~a: |
|||||
~a = ~a1 + ~a2 = ~a3 + ~a4 + ~a5 = ~a6 + ~a7 + ~a8 + ~a9 + ~a10: |
|||||
Не единственным может оказаться и представление вектора |
|||||
~a в виде линейной комбинации "1~a1 +"2~a2 +: : :+"n~an; заданного |
|||||
набора векторов ~a1;~a2; : : : ;~an: ~a = "1~a1 + "2~a2 + : : : + "n~an; ãäå |
|||||
"1; "2; : : : ; "n некоторые числа. |
|
||||
В качестве примера на рис. 24 показаны три представления |
|||||
вектора ~a в виде линейных комбинаций векторов ~a3; ~a4; ~a5 (êîì- |
|||||
планарных с ~a): |
|
|
|
||
|
~a = ~a3 + ~a4 + ~a5 = 2~a3 + 0~a4 + 2~a5 = 2~a3 + 4~a4 2~a5: |
||||
|
|
~a8 |
~a9 |
4~a4 |
|
|
|
|
2~a5 |
2~a5 |
|
|
~a7 |
|
|
||
|
|
|
2~a3 |
||
|
~a6 |
~a1 |
~a2 ~a10 |
|
2~a3 |
|
|
~a |
|
~a |
|
|
|
|
|
|
|
|
~a3 |
~a4 |
~a5 |
~a3 |
~a5 |
|
|
|
~a4 |
||
|
|
Ðèñ. 23 |
|
Ðèñ. 24 |
|
|
|
|
|
|
|
Геометрические векторы, складываемые по правилу параллелограмма, как было показано в предыдущем параграфе, являются примером линейного пространства. Поэтому всякий вектор ~a можно единственным образом представить в виде линейной комбинации базисных векторов. И задача единственного разложения вектора сводится к выбору подходящего базиса.
38 |
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
4.1.Векторный базис. В тр¼хмерном пространстве
векторный базис образует любая тройка некомпланарных век-
~ |
~ |
~ |
|
|
|
|
|
торов b1 |
; b2 |
; b3: Для доказательства этого утверждения доста- |
|||||
|
|
|
|
|
~ |
~ |
~ |
точно показать, что три некомпланарных вектора b1 |
; b2 |
; b3 ëè- |
|||||
нейно независимы. |
|
|
|
|
|
||
Предположим противное, то есть выполняется равенство |
|||||||
|
|
~ |
~ |
~ |
~ |
|
|
|
|
b1 |
+ b2 |
+ b3 |
= 0; |
|
|
в котором хотя бы один из числовых коэффициентов не равен
нулю. Пусть 6= 0: Тогда вектор |
|
~ |
|
можно выразить в виде |
||||
|
b1 |
|||||||
|
~ |
|
~ |
: |
||||
линейной комбинации векторов b2 |
è b3 |
|||||||
~ |
|
|
~ |
|
|
|
~ |
|
b1 |
= |
|
b2 |
|
|
b3: |
||
Отсюда (сравни с условием (1.3)) следует компланарность век-
~ ~ ~
торов b1; b2; b3, что противоречит исходному условию. Следовательно, всякий вектор ~a может быть единствен-
ным образом разложен на три составляющие, параллельные
|
|
|
~ |
~ |
~ |
; |
соответственно трем некомпланарным векторам b1 |
; b2 |
; b3 |
||||
~ |
~ |
~ |
; |
|
(1.46) |
|
~a = a1b1 |
+ a2b2 |
+ a3b3 |
|
|||
где числа a1; a2 è a3 называются координатами вектора ~a в
~ ~ ~
базисе b1; b2; b3.
Докажем однозначность определения координат вектора ~a в разложении (1.46). Если предположить противное, то есть су-
|
|
|
|
|
|
|
|
|
|
|
0 ~ |
ществует хотя бы еще одно разложение, например, ~a = a1b1 + |
|||||||||||
0 ~ |
0~ |
то, вычитая это равенство из (1.46), мы бы получили |
|||||||||
a2b2 +a3b3; |
|||||||||||
|
|
~ |
|
0 ~ |
|
|
0 ~ |
|
0 ~ |
||
|
|
0 = (a1 a1)b1 + (a2 a2)b2 + (a3 a3)b3: |
|||||||||
Пусть, например, |
|
|
0 |
|
|
|
|
~ |
|||
a1 6= a10. Тогда вектор0 |
b1 можно выразить |
||||||||||
|
~ |
~ |
~ |
|
a2 a2 |
~ |
|
a3 a3 |
~ |
|
|
через |
b2 è |
b3 : b1 |
= |
a0 |
a1 |
b2 |
+ |
a0 a1 |
b3: Последнее равенство |
||
|
|
|
|
1 |
|
|
1 |
|
|
||
|
|
|
|
~ |
~ |
|
~ |
|
|
|
|
означает, что векторы b1; b2 è b3 компланарны, что противоре- |
|||||||||||
чит условию0 |
векторного0 |
|
базиса. Поэтому все разности (a1 a10 ); |
||||||||
(a2 a2); (a3 |
a3) должны быть равны нулю, и, следовательно, |
||||||||||
разложение (1.46) единственно.

Ÿ 4. Разложение вектора на составляющие |
39 |
Для геометрического нахождения координат вектора нужно поступить следующим образом. Отложим все четыре вектора ~a;
~ |
~ |
~ |
от общего начала и проведем через конец A вектора ~a |
b1 |
; b2 |
è b3 |
плоскости, параллельные граням трехгранного угла, образован-
~ ~ ~
ного векторами b1; b2; b3: Эти плоскости, линии пересечения которых с гранями трехгранного угла показаны на рис. 25 штри-
|
|
~ |
~ |
~ |
~ |
; |
хованными линиями, отсекают на осях b1 |
; b2 |
; b3 |
; векторы a1b1 |
|||
~ |
~ |
, которые, согласно определению сложения векторов, |
||||
a2b2 |
; a3b3 |
|||||
являются составляющими вектора ~a. В результате получается
разложение (1.46). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
è |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если векторы aibi |
bi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
||
одинаково направлены, |
òî |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
координата |
ai равна отно- |
|
b3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шению jaibij=jbij. Åñëè âåê- |
|
a3~b3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
òîðû aibi è |
bi противопо- |
|
|
|
|
|
|
|
|
~a |
||||||||||||||||
|
~ |
~ |
|
|
|
|
|
|
|
|
|
|||||||||||||||
ложны, то ai = jaibij=jbij. |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
На рис. 25 представлен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
a2b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
случай, когда координаты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
~ |
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
||||||||
a1; a2 è a3 |
удовлетворяют |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
b1 |
a1b1 |
||||||||||||||||||||||
условиям: a1 > 1; a2 < 0 è |
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ðèñ. 25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
0 < a3 < 1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.2. Свойства координат вектора. Один и тот же вектор в разных базисах обладает различными координатами. Отметим три важных свойства координат векторов, которые не зависят от выбора базиса и непосредственно следуют из единственности разложения вектора по трем базисным векторам, а именно:
1) если два вектора равны друг другу, то их координаты в одном и том же базисе равны между собой, и наоборот, из равенства координат двух векторов следует равенство самих векторов:
~ ~ |
= B1; A2 = B2; A3 |
= B3: |
(1.47) |
A = B () A1 |
2) Координаты геометрической суммы нескольких векторов равны алгебраическим суммам координат слагаемых векторов.
40 |
Глава 1. |
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
|||||
Для доказательства этого утверждения заметим, что век- |
|||||||
|
|
~ |
~ ~ |
|
~ |
|
|
торное равенство A = B + C + : : : + G эквивалентно следующе- |
|||||||
ìó: |
|
|
|
|
|
|
|
3 |
|
3 |
|
3 |
|
3 |
|
X |
~ |
X |
~ |
X |
~ |
X |
~ |
|
Aj bj = Bj bj + Cj bj + : : : + Gj bj ; |
||||||
j=1 |
|
j=1 |
|
j=1 |
|
j=1 |
|
ãäå Aj ; Bj ; Cj ; : : : ; Gj (j = 1; 2; 3) координаты векторов в ба-
~ |
; |
~ |
; |
~ |
: Используя свойства (1.5) и (1.8), перепишем по- |
|||
çèñå b1 |
b2 |
b3 |
||||||
следнюю формулу в виде |
|
|
||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
X |
~ |
~ |
(1.48) |
|
|
|
|
|
|
(Aj Bj Cj : : : Gj )bj = 0: |
||
j=1
~
Базисные векторы bj линейно независимы. Значит, равенство (1.48) возможно только, если выражения, стоящие в круглых скобках, будут равны нулю. Итак доказали, что
|
åñëè |
|
~ ~ |
~ |
~ |
|
|
|
|
A = B + C + : : : + G; |
|
|
|||
|
òî |
Aj = Bj + Cj + : : : + Gj ; |
j = 1; 2; 3: |
(1.49) |
|||
3) Умножение вектора на скаляр эквивалентно умноже- |
|||||||
нию всех его координат на тот же скаляр: |
|
||||||
|
3 |
|
|
|
|
|
|
~ |
X |
~ |
~ |
~ |
~ |
(1.50) |
|
A = |
|
Aj bj = ( A1 )b1 |
+ ( A2 )b2 |
+ ( A3)b3: |
|||
|
j=1 |
|
|
|
|
|
|
Это свойство непосредственно вытекает из распределитель- |
|||||||
ности суммы векторов (см. формулу (1.7)). |
|
||||||
4.3. Размерность |
векторного множества. |
Ðàñ- |
|||||
смотрим множество векторов, лежащих в некоторой плоскости. Возьмем в качестве базисных векторов любые два неколлине-
~ |
|
|
арных вектора ~g и h, лежащих в рассматриваемой плоскости, |
||
~ |
~ |
~ |
обозначим их, например, b1 |
= ~g è b2 |
= h. Тогда в качестве тре- |
~ |
может выступать любой вектор, не |
|
тьего базисного вектора b3 |
||
компланарный той же плоскости.
~
Очевидно, что третья координата любого вектора f из рассматриваемого множества в данном базисе будет равна нулю, и
