
Беляев Ю.Н. Введение в векторный анализ
.pdf
Ÿ 2. Векторное поле |
161 |
из параллельного переноса, поворота как тв¼рдого тела и деформаций. Можно показать, что и в этом случае вихрь скорости ~v равен удвоенной угловой скорости вращения !~ элемента жидкости. Поэтому вектор 2!~ ещ¼ называют вектором завихр¼нности движения.
~
Аналогично rot P характеризует закрученность векторных
~
линий поля P .
2.6.Потенциальное векторное поле. Скалярный по-
тенциал. |
Пусть векторное поле |
~ |
определено в области . |
|
P |
||||
|
|
|
~ |
|
Если циркуляция векторного поля P по любому замкнутому |
||||
контуру L 2 |
|
|
~ |
|
равна нулю, векторное поле P называется |
||||
п о т е н ц и а л ь н ы м. Это определение эквивалентно следующим тр¼м.
1) Необходимым и достаточным условием потенциально-
~ |
|
|
|
сти векторного поля P |
в области является равенство |
||
|
~ |
~ |
(3.43) |
|
rot P = 0 |
||
во всех точках области . Это следует из определения вихря (3.31).
2) Криволинейный интеграл от потенциального векторно-
ãî ïîëÿ ~ не зависит от вида кривой интегрирования , а
P L
определяется положением начальной и конечной точек интегрирования.
Действительно, возьм¼м две кривые L1 2 è L2 2 , на- чинающиеся в одной точке A 2 и заканчивающиеся в точке B 2 . Образуем замкнутый контур L = L1 + L2 , ãäå L2 уча- сток интегрирования от B до A по кривой L2 (в направлении, противоположном показанному на рис. 86).
B
L2
L1
A
Ðèñ. 86
Если использовать свойство (3.25), легко показать взаимосвязь двух формул:
Z |
Z |
I |
||
|
~ |
|
~ |
~ |
|
P d~r = |
|
P d~r , |
P d~r = 0: |
L |
1 |
L |
2 |
L |
|
|
|
||
162 |
Глава 3. ФУНКЦИИ ТОЧКИ |
~
3) Векторное поле P называется п о т е н ц и а л ь н ы м, если
~
P является градиентом некоторой скалярной функции ':
~
P = grad ':
~
Величина ' скалярный потенциал поля P .
~
Покажем, что интеграл от поля P = grad ' не зависит от кривой интегрирования. По определению градиента, под знаком интеграла будет полный дифференциал d' = grad ' d~r, и, следовательно, интегрирование по кривой L даст приращение функции ', обусловленное перемещением из начальной точки A кривой L в конечную точку B.
Z Z Z
~
P d~r = grad ' d~r = d' = '(B) '(A): (3.44)
L L L
П р и м е р 72. Покажем, что силы, которые в каждой точке пространства направлены по прямой, соединяющей м.т. с одним и тем же центром, а их величина зависит только от расстояния до этого центра, являются потенциальными.
Если центр выбрать за начало отсч¼та, то такую силу можно записать в виде
~
F = F (r)~r:
Частный случай такой силы был рассмотрен в примере 71. Воспользуемся условием потенциальности поля в форме
(3.43). В декартовой системе координат это условие примени-
~
тельно к полю F можно переписать в виде тр¼х равенств:
|
@Fz |
|
= |
@Fy |
; |
@Fx |
= |
@Fz |
; |
|
|
@Fy |
|
= |
@Fx |
: |
(3.45) |
|||||||||
|
@y |
@z |
|
|
|
|
@x |
@y |
||||||||||||||||||
|
|
|
|
@z |
@x |
|
|
|
|
|
|
|
||||||||||||||
Вычислим частные производные от проекций силы Fz è Fy |
||||||||||||||||||||||||||
по координатам y и z соответственно: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
@Fz |
= |
|
@ |
|
(F (r)z) = z |
@F (r) @r |
= |
|
@F (r) zy |
; |
||||||||||||||
|
|
@y |
|
@y |
|
@r |
|
@y |
|
@r |
|
|
r |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
@Fy |
|
= |
|
@ |
|
(F (r)y) = y |
@F (r) @r |
= |
|
@F (r) yz |
: |
|||||||||||||
|
|
@z |
|
|
@z |
|
@r |
|
@z |
|
@r |
|
|
r |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||

Ÿ 3. Поток векторного поля |
163 |
Очевидно, что первое из соотношений (3.45) выполняется. Точ- но так же проверяется справедливость двух других равенств (3.45).
~
Сила F = F (r)~r есть частный случай центральной силы
~
F = F (x; y; z)~r; которая в общем случае не является потенциальной.
Задачи |
|
|
|
||
|
90. |
|
~ |
: 1) |
~ |
|
Найти векторные линии поля P |
P (M ) = y~ex + x~ey |
|||
2) |
~ |
|
~ |
|
~ |
P (M ) = x~ex y~ey ; 3) |
P (M ) = x~ex + 2y~ey ; 4) P (M ) = x~ex + |
||||
y~ey + z~ez : |
|
|
|
||
|
91. |
|
~ |
|
|
|
Вычислить работу силы F = y~ex x~ey по перемещению |
||||
м.т. вдоль кривой ~r = R cos3 t~ex + R sin3 t~ey от точки A(t = 0)
до точки B(t = =2). |
|
|
|
~ |
|||
92. |
Вычислить циркуляцию векторных полей : 1) |
||||||
P (M ) = |
|||||||
2 |
|
~ |
|
|
~ |
|
|
y~ex + x |
~ey + z~ez , 2)P (M ) = z~ex + x~ey + y~ez , 3)P (M ) = y~ex x~ey + |
||||||
z~ez , по контуру ` : x2 + y2 = R2; z = 0: |
|
||||||
93. Проверить потенциальность полей: |
|
||||||
~ |
3 |
3 |
~ey + z |
3 |
~ez ; |
|
|
1) P (M ) = x |
~ex y |
|
|
||||
~ |
|
|
|
|
|
|
|
|
|
|
|
2) P (M ) = yz(2x + y + z)~ex + xz(x + 2y + z)~ey + xy(x + y + 2z)~ez ; |
|||||||||||
~ |
|
y |
|
|
x |
|
|
|
|
|
|
3) P (M ) = |
x2 + y2 |
~ex + |
x2 + y2 |
~ey : |
|
|
|
||||
94. Вычислить вихрь векторного поля: |
|
|
|||||||||
~ |
|
|
|
|
|
|
|
|
~ |
|
|
1) P (M ) = xyz(~ex + ~ey + ~ez ); |
|
|
7) P (M ) = (~c ~r)~r; |
||||||||
~ |
2 |
|
2 |
2 |
~ez ; |
|
|
~ |
2 |
~r; |
|
2) P (M ) = z |
~ex + x |
~ey + y |
|
|
8) P (M ) = (~c ~r) |
||||||
~ |
|
2 |
|
|
|
2 |
)~ez ; |
~ |
|
|
|
3) P (M ) = (xy +z |
)~ex +(xz +y |
9) P (M ) = (~r ~r)~c; |
|||||||||
~ |
|
|
|
|
|
|
|
|
~ |
|
|
4) P (M ) = u(r)~c; |
|
|
|
|
|
|
10) P (M ) = ~c=(~c ~r); |
||||
~ |
|
|
|
|
|
|
|
|
~ |
|
|
5) P (M ) = ~c sin br; |
|
|
|
|
|
11) P (M ) = ~r=(~c ~r); |
|||||
~ |
n |
~ex; |
|
|
|
|
|
|
~ |
|
|
6) P (M ) = r |
|
|
|
|
|
|
12) P (M ) = u(r)~r: |
||||
Ÿ 3. Поток векторного поля
Другой существенной характеристикой векторного поля наряду с вихрем является понятие потока3 вектора, смысл кото-
3Понятие поток введено Максвеллом в работе 1873 года ½A treatise on electricity and magnetism\, посвящ¼нной теории электромагнетизма.
164 |
Глава 3. ФУНКЦИИ ТОЧКИ |
рого, как и смысл вихря, наиболее наглядно демонстрируется на примере поля скоростей.
3.1. Поток скорости это объ¼м сплошной среды (например, жидкой), протекающий через некоторую неподвижную поверхность за единицу времени. Рассмотрим
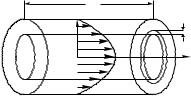
П р и м е р 73. Найд¼м объ¼м жидкости (или газа) протекающей по цилиндрической трубке радиуса R и длиной L под влиянием перепада давлений p на концах трубки.
Скорость ~v течения жидкости направлена везде вдоль оси трубки, а по величине меняется в перпендикулярном оси направлении в зависимости лишь от одной координаты расстояния r от оси.
Сила трения, действующая на объ¼м жидкости, ограниченной цилиндрической поверхностью некоторого радиуса r < R (на рис. 87 эта поверхность показана штрихованной линией), согласно закону Ньютона для внутреннего трения, равна
~ |
d~v |
|
d~v |
|
Fòð = |
dr |
S = |
dr |
2 rL; |
где коэффициент вязкости жидкости, S = 2 rL площадь боковой поверхности выделенного цилиндра. Эта сила компенсируется силой перепада давлений, приложенных к основанию цилиндра и равной r2 p. Приравнивая эти силы, получим уравнение
L |
R |
dv |
|
p |
|
|
|
= |
|
r: |
( ) |
dr |
2L |
|||
r |
dr |
Между поверхностью тв¼р- |
|
||
|
|
|
0 |
|
дого тела и жидкостью всегда |
|
v(r) |
|
|
|
существуют силы молекулярно- |
|
|
го сцепления, приводящие к то- |
Ðèñ. 87 |
|
му, что непосредственно приле- |
|
гающий к тв¼рдой стенке слой |
|
|
|
жидкости полностью задерживается, как бы ½прилипая\ к ней. С уч¼том того, что скорость на самой поверхности трубы
(r = R) равна нулю, получаем решение уравнения ( ):

Ÿ 3. Поток векторного поля |
165 |
v(r) = p R2 r2 :
4L
Таким образом, скорость жидкости в трубке меняется по квадратичному (параболическому) закону от нуля на стенке трубы до максимального значения на оси трубки (см. рис. 87).
Объ¼м жидкости dV , вытекающий в единицу времени че- рез площадь d кольца радиуса r и шириной dr равен dV = v(r)d = v(r)2 rdr. Следовательно, объ¼м жидкости V , вытекающей за единицу времени через вс¼ сечение трубки R2, равен
R |
R |
|
|
|
|
|
|
V = Z |
v(r)d = Z |
|
R2 |
r2 |
2 rdr = |
|
p : |
4L |
8L |
||||||
0 |
0 |
p |
|
|
|
R4 |
|
|
|
|
|
|
|||
В рассмотренном примере задача вычисления потока через поперечное сечение трубки облегчалась тем, что, во-первых, вектор скорости ~v был перпендикулярен поверхности во всех е¼ точках, во-вторых, поверхность , через которую истекал поток, была плоской.
~eni
i
~v
Ðèñ. 88
Vi
В общем случае для вычисления потока через поверхность последнюю нужно разбить на малые площадки i, такие, чтобы можно было считать вектор ~v в каждой точке i одним и тем же, а сами участки плоскими c единич- ным вектором нормали ~eni. Тогда поток через элементарную площадку равен объ¼му цилиндра с площадью основания i и высотой v cos(~v; ~eni):
d
= iv cos(~v; ~eni) = ~v ~eni i:
На рис. 88 этот цилиндр показан штрихованным контуром. Объ¼м V жидкости, вытекающей через всю поверхность ,
это сумма объ¼мов Vi, когда число участков разбиения
166 Глава 3. ФУНКЦИИ ТОЧКИ
неограниченно возрастает при уменьшении максимальной площадки до нуля:
|
k |
|
|
|
|
|
i |
X |
|
~e |
|
|
: |
V = lim |
~v |
|
ni |
|||
k!1 |
|
|
i |
|
max j j!0 i=1
Аналогично определяется
3.2.Поток векторного поля. Пусть в каждой точке
~
M поверхности определено векторное поле P (M ): Мысленно разобъем поверхность на частичные поверхности i; площади которых обозначим через i. Выберем на каждой из частич- ных поверхностей i по произвольной точке Mi и определим в ней единичный вектор положительной нормали ~en(Mi).
Образуем сумму
X |
~ |
(3.46) |
|
P (Mi) ~en(Mi) i : |
i
Если существует предел суммы (3.46) при стремлении к нулю максимальной площади участка разбиения поверхности , не зависящий ни от способа разбиения поверхности , ни от выбора точек Mi, то он называется потоком N векторного поля
~
P (M ) через поверхность :
Xk ~
N = lim P (Mi ) ~en(Mi ) i ; (3.47)
k!1
max j ij!0 i=1
и обозначается
ZZ ZZ
~ ~ ~
N = P ~end = P d ; (3.48)
~
ãäå d = ~end вектор, модуль которого равен величине площади элементарной площадки d , а направление совпадает с единичным вектором нормали к площадке ~en.
Отметим очевидное свойство потока векторного поля: поток суммы полей через некоторую поверхность равен сумме
Ÿ 3. Поток векторного поля |
167 |
потоков каждого из полей в отдельности через ту же поверхность.
Вычисление потока векторного поля сводится к вычислению поверхностного интеграла первого рода, который, в свою оче- редь, к вычислению двойного интеграла. Именно поэтому в обозначении (3.48) потока N используется двойной знак интеграла.
3.3. Нормаль к поверхности. Для вычисления потока вектора через поверхность необходимо определить нормаль к повехности. Напомним, как это делается.
Пусть дана поверхность , определяемая уравнением
F (x; y; z) = 0: |
(3.49) |
Уравнение (3.49) это уравнение поверхности нулевого уровня функции F (x; y; z). Следовательно, нормалью к поверхности в точке M является градиент функции F (M )
~n = grad F (M ) = |
@F |
~ex + |
@F |
~ey + |
@F |
~ez ; |
(3.50) |
|
|
|
|||||
@x |
@y |
@z |
Единичный вектор нормали к поверхности
|
~n |
|
|
|
|
|
|
|
|
|
@F |
|
|
|
|
|
|
|
|
|
|
|
~en = |
= |
|
|
|
|
|
|
|
|
@x |
|
|
|
|
|
|
|
~ex + |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
~n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
r |
|
|
2 |
|
|
2 |
|
|
@z |
2 |
|
||||||||||
|
j j |
|
@x |
+ |
@y |
+ |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
@F |
|
|
|
@F |
|
|
|
|
@F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
@F |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
r @x |
|
|
@y |
|
|
|
|
|
|
|
|
~ey + |
|
|||||
|
|
|
|
+ |
@y |
|
2 |
+ |
@z |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
@F |
|
2 |
@F |
|
|
@F |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
@F |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
@z |
|
|
|
|
|
|
|
|
~ez : |
(3.51) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
r @x |
|
+ |
@y |
|
2 |
+ |
@z |
|
|
||||||||||
|
|
|
|
|
|
|
|
@F |
|
2 |
@F |
|
|
@F |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Если уравнение поверхности разрешено относительно одной из координат, например
z = f (x; y); èëè z f (x; y) = 0;
168 |
|
|
|
|
|
Глава 3. |
ФУНКЦИИ ТОЧКИ |
|||
òî |
|
|
|
|
|
|
|
|
|
|
|
@F |
= |
@f |
; |
@F |
= |
@f |
; |
@F |
= 1; |
|
|
|
|
|
|
|||||
|
@x |
@x |
@y |
@y |
@z |
|||||
и направляющие косинусы единичного вектора нормали по отношению к координатным осям x; y; z равны
d |
q |
|
@f |
|
|
|
|
; |
> |
|
|||
|
@f |
|
|
|
|
|
|||||||
cos(~en; ~ex) = |
|
|
|
|
@x |
|
|
|
|
> |
|
||
|
|
|
|
|
@y |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
( @x@f )2+ @f@y |
|
2 +1 |
|
9 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
@x ) |
2 |
|
|
|
|
2 |
|
|
|
||
d |
|
|
|
|
1 |
|
|
|
|
|
; |
= |
(3.52) |
cos(~en; ~ey ) = |
|
|
|
|
|
|
|
|
|
|
> |
||
|
|
|
@f |
|
|
|
@f |
|
|
|
|
> |
|
|
|
|
|
|
+ |
|
|
|
|
+1 |
|
> |
|
|
|
|
|
|
|
|
|
|
|
> |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
d |
|
|
|
|
|
|
|
|
|
|
|
> |
|
q |
|
|
|
|
|
|
|
|
|
|
> |
|
|
cos(~en; ~ez ) = |
q |
|
|
|
|
|
|
|
|
|
: |
> |
|
|
( |
@f |
2 |
|
|
@f |
|
2 |
|
|
> |
|
|
|
@x ) |
|
+ |
|
@y |
|
|
+1 |
|
> |
|
||
3.4.Вычисление потока. Пусть поверхность задана
âдекартовой системе координат xyz однозначной функцией z =
f (x; y).
~
Представим векторное поле P и единичный вектор нормали ~en к поверхности через их проекции на оси декартовой системы координат:
~ |
|
|
|
|
P = Px~ex + Py~ey + Pz~ez ; |
d |
d |
||
|
n |
d |
||
~e |
|
= cos(~en; ~ex)~ex + cos(~en; ~ey )~ey + cos(~en; ~ez )~ez ; |
||
d
где направляющие косинусы cos(~en; ~ei) (i = x; y; z; ) определяются формулами (3.52). Обозначим
~ |
|
|
n |
x |
d |
d |
d |
u(x; y; z) = P |
|
~e |
|
= P |
cos(~en; ~ex)+Py cos(~en; ~ey)+Pz cos(~en; ~ez):(3.53) |
||
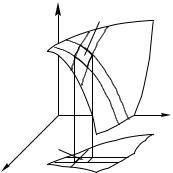
Проекцией поверхности на плоскость xy (см. рис. 89) является плоская площадка D. Мысленно рассеч¼м поверхностьсистемами плоскостей, параллельных координатным плоскостям xz и yz на элементарные площадки d . На рис. 89 штрихованными линиями показаны следы четыр¼х рассекающих плоскостей, выделяющих одну из элементарных площадок d и е¼ проекцию dD на плоскость xy.
Ÿ 3. Поток векторного поля
z
~en
d
y
xdD  D
D
Ðèñ. 89
169
Проекция dD площадки d на плоскость xy равна dD = dxdy. Очевидно, что
d dD = d cos(~en; ~ez );
и, следовательно,
d = |
|
dD |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|||
|
d |
|
|
|
|
||||
|
|
|
|
|
|
|
|||
|
cos(~en; ~ez ) |
|
|
|
|||||
|
|
|
|
|
|
|
|
||
=s1+ |
@f |
2 |
@f |
2 |
|
||||
+ |
dxdy: |
||||||||
|
|
||||||||
@x |
@y |
||||||||
~
При вычислении потока нужно брать значения поля P в точках на поверхности . Заменим координату z в подынтегральной функции (3.53), используя уравнение поверхности z = f (x; y). В результате формулу для потока векторного поля можно представить в виде двойного интеграла
N = ZZ |
P~ ~end = ZZ |
u(x; y; z)d = |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
u (x; y; f (x; y)) s1 + |
@f |
|
2 |
|
|
@f |
2 |
|
||
= ZZ |
|
|
+ |
|
dxdy; (3.54) |
||||||
|
|
|
|||||||||
@x |
|
@y |
|||||||||
D
вычисляемого по проекции D поверхности на плоскость xy. Подставим выражения (3.52) и (3.53) в формулу (3.54) и перепишем последнюю в виде
|
@f |
|
@f |
|
dxdy : |
0 |
|
|
|
|
|
||
N = ZZ Pz Py @y |
Px |
|
|
|
||
@x |
z=f (x;y) |
(3:54 ) |
||||
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П р и м е р 74. Применим формулу (3:540) к решению следу-
~
ющей задачи. Найд¼м поток поля P = x~ex + 2y~ey + z~ez через часть плоскости x + 2y + 3z = 1, отсекаемой координатными поверхностями xy, yz, xz, в направлении нормали, образующей острый угол с осью Oz.
Перепишем уравнение поверхности в виде
170 |
Глава 3. ФУНКЦИИ ТОЧКИ |
|
1 |
1 |
|
2 |
|
|
|
|
|
1 |
1 |
|
2 |
|
||||
z = |
|
|
|
x |
|
y; т.е. в данном случае f (x; y) = |
|
|
|
x |
|
y: |
||||||
3 |
3 |
3 |
3 |
3 |
3 |
|||||||||||||
Находим частные производные: @f@x = 31 , @f@y = 32 . |
|
|
||||||||||||||||
|
|
Pz Py @y |
Px @x |
z=f (x;y) = |
3 (1 2x + 2y): |
|
|
|||||||||||
|
|
|
|
|
|
|
@f |
|
@f |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Координатные поверхности xy, yz, xz отсекают от плоскости x + 2y + 3z = 1 треугольник ABC (рис. 90), вершины которого имеют координаты A(1; 0; 0), B(0; 1=2; 0), C(0; 0; 1=3).
Вычисляем поток по формуле (3:540):
N = 3 |
OABZ Z |
(1 2x + 2y)dxdy = |
3 |
1 |
21 |
21 x |
||||
Z dx |
Z |
(1 2x + 2y)dy = 18 : |
||||||||
1 |
|
|
1 |
|
|
|
1 |
|
||
|
|
|
|
|
0 |
0 |
|
|
|
|
3.5.Поток через замкнутую поверхность. Ïðè ðàñ-
~
смотрении потока векторного поля P через замкнутую поверхность в обозначении (3.48) вместо символа
|
z |
|
|
ZZ |
ZZ |
|
|
|
|||
|
|
|
|
||
C |
|
|
|
будем использовать ; |
|
|
|
B |
|
а именно |
|
O |
|
y |
|
||
|
ZZ |
ZZ |
|||
|
|
|
|
||
A |
|
|
~ |
~ ~ |
|
|
|
N = P ~end = P d : |
|||
x |
Ðèñ. 90 |
|
В качестве вектора ~en здесь подразумевается единичный вектор внешней нормали к объ¼му, ограниченному поверхностью .
Задачи
95. |
~ |
2 |
2 |
)~ex + |
Вычислить поток векторного поля P (M ) = (x |
|
+ y |
(y2 + z2)~ey + (z2 + x2)~ez : 1)через часть плоскости OXY , ограниченную окружностью x2 + y2 = 1, в направлении вектора ~ez
