Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сыктывкарский Государственный Университет им. Питирима Сорокина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Беляев Ю.Н. Введение в векторный анализ

.pdf

Скачиваний:

401

Добавлен:

29.03.2016

Размер:

1.13 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2122 / 2222

Ответы и решения

211

AB и осью Ox через ', то cos ' =

31. Если обозначить угол между !

4=5, sin ' = 3=5; j!j

= 5.

32.

! !

8~e

8) + 4

6 = 0.

AB = 3~e

+ 4~e

, CD =

+ 6~e

, AB CD = 3

(

AB и CD равен 90

Следовательно, угол между векторами !

33. 21=13:

34. Вычитая из координат точки B координаты точки A, находим

AB = 3~e

7~e

Оба направляющие косинусы биссектрисы первого координатно-

го угла равны

, следовательно, единичный вектор ~e` îñè `; íà êîòî-

= p

+ p

AB, åñòü ~e

. Таким

рую нужно спроектировать вектор !

образом, (AB)` = !

= 3

35.D(4; 0; 6).

36.45 èëè 135 :

37.

~c = 16~a + 6b:

38. j!j

= 3

39. x = y = z = 2:

40.

M (3 2; 3; 3):

41.

AD = 2(AC

AB):

42.

~c =

~a +

43.

135 :

z j!j

44.

+2~e

= 3;

AB =

2~e ; AB

= 3; AC =

2~e

+~e

+2~e ; AC

!		!	6
AB		AC = 0; следовательно,			A = 90		. ABC равнобедренный,

значит, два других угла 6 B = 6 C = 45 .

45. 90 .

50. Пусть стороны параллелограмма ABCD (рис. 103) определя-

ются векторами ~a =

AB = DC и b = AD = CB. Тогда диагонали его

представляют векторы ~a + b =

è ~a

b = DB:

Вычислим квадраты длин диагоналей:

; ~a

j~a + bj

= (~a + b) (~a + b) = a

+ 2ab cos(~a; b) + b

~ 2

= (~a

(~a

b) = a

~a; b) + b

Складывая эти равенства, находим:

= 2(a

)

j~a + bj

+ j~a bj

+ b

Ðèñ. 103

сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

51. Опустим из вершин A и B треугольника ABC (см. рис. 104) высоты на стороны BC и CA. Обозначим точку пересечения этих высот буквой D. Для решения задачи нужно показать, что прямая, проведенная через точки C и D, будет перпендикулярна стороне AB.

Выпишем очевидные векторные равенства

212	Ответы и решения

	!		!	!			C
	!		!	!
	AD		BD = AB;
	!		!	!		D
	CD	DB = BC;
	!		!	!
	AD		DC = CA:
				AD ê BC è
Условие перпендикулярности !					!	Ðèñ. 104
!	!				A	Ðèñ. 104	B
BD ê CA äàåò:					A		B
BD ê CA äàåò:

0 =

! !

BC = AD

(CD

DB) = AD

AD DB;

0 =

! !

BD CA = BD

(AD

DC) = BD AD

BD DC:

Вычитая из первого равенства второе, найдем

AD CD + BD DC = CD

(AD

BD) = CD AB = 0;

и, следовательно, !

перпендикулярен AB; так что точка D лежит

на высоте, опущенной из вершины C.

52.135

53.60 :

54.Сфера радиуса R = j~r ~aj.

56.80.

57.3=2.

58. ~a b = 9.

~ ~

59. jA + Bj = 15, jA Bj =

113:

60. Обозначим ( ~a) b

= ~c и (~a b) = d. Для доказательства

равны по модулю

равенства (1.117) нужно показать, что векторы ~c и d

и одинаково направлены.

~c;

~a; <0

~a b

~a; >0

~c;

Ðèñ. 105

По определению умножения вектора на число, векторы ~a и ( ~a)

коллинеарны. Поэтому если

и равенство

~akb, èëè = 0, òî ~c = 0, d = 0

(1.117) выполняется.

Ответы и решения

213

Пусть векторы ~a и b не коллинеарны и направлены под углом '

друг к другу. Тогда ~c и d перпендикулярны одной и той же плоскости

p, в которой лежат векторы ~a и b, и направлены в одну сторону при

любом =6 0 (см. рис. 105). Длины векторов ~c и d также совпадают: c = d = ab sin '. Таким образом, свойство (1.117) справедливо и в этом случае.

61.

	~	~a
	~
	b
Ðèñ. 106		~e1
Ðèñ. 106
~	~e2
bp		~e3
		~e3
p	~
p	~a b

Выберем на рис. 106 направления тройки взаимно ортогональных единичных векторов так, чтобы вектор ~e1 был направлен по вектору ~a, вектор ~e3 - перпендикулярен плоскости, в которой лежат векто-

~	? ~a;	~
ðû ~a è b (~e3	? ~a;	~e3 ? b) è

~e2 = ~e3 ~e1: Обозначим через

bp = b sin (~a; b) - проекцию век-

тора b на проскость p; перпен-

дикулярную ~a. Тогда bp = bp~e2 и в соответствии с (1.117) можем записать

	~			~
	~a b = abp~e3	= abp(~e1 ~e2) = (a~e1) (bp~e2) = ~a bp: ( 1)
Для доказательства формулы (1.118) заменим ее следующей це-
почкой равенств:
~	~	~	~	~
~a (b+~c) = ~a (b+~c)p = ~a (bp +~cp) = ~a bp +~a ~cp				= ~a b+~a ~c: ( 2)

Первое и последнее равенства в этой формуле непосредственно следуют из свойства ( 1). Второе равенство в формуле ( 2) есть следствие свойства проекции вектора на плоскость. Наконец, докажем предпоследнее равенство в формуле ( 2):

~ ~

~a (bp + ~cp) = ~a bp + ~a ~cp:

Для этого обратимся к рис.107, на котором изображены: векторы

~	~	~					~
bp, ~cp,	bp + ~cp ; вектор	~a bp, перпендикулярный					bp; вектор ~a ~cp,
			AD, равный по построению сумме
перпендикулярный ~cp, и вектор !
	~
векторов ~a bp è ~a ~cp , ò.å.
		!		~	p	p
		AD = ~a		b + ~a		~c :	(	3)

214

Ответы и решения

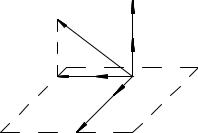
Все эти векторы лежат в одной плоскости p, перпендикулярной

j~a ~cpj = acp и параллелограммы

вектору ~a. Поэтому j~a bpj = abp;

= b

ABDC

подобны. Следовательно, AD

+ ~c ; è

0 =

0 ; òî åñòü

AD = ~a

+ ~c ):

(

Равенства ( 3) и ( 4) дают требуемое доказательство.

~cp

~a ~cp

~a bp

Ðèñ. 107

62.

~e2 ~e3 = ~e1;

~e1 ~e1 = 0;

~e2 ~e2 = 0;

~e3 ~e3 = 0; ~e1 ~e2 = ~e3;

~e3 ~e1 = ~e2:

63.1) M0 = ~r F = 140~ez; 2) d = 2:8 ì.

64.По определению центра масс,

	N			N			N
~rc =	i=1 mi~ri		=	i=1 mi~ri	;	и, следовательно, ~vc =	i=1 mi~vi	:
	P	N		P M			P M

	P i=1 mi

Радиус-вектор ~ri i-й точки можно представить в виде ~ri = ~rc +~rci; ãäå ~rci радиус-вектор i-й точки относительно центра масс. Соответственно, если обозначить ~vci скорость i-й точки относительно центра масс, то ~vi = ~vc + ~vci :

Подставим эти выражения в определение момента количества движения системы:

K = mi (~rc + ~rci) (~vc + ~vci ):

i=1

68. В полярной системе координат

h i r = r0 exp (' '0) ctg ;

ãäå r0 è '0 координаты м.т. в начальный момент времени.

Ответы и решения

215

69.

x2 + y

71. vr = r;

v' = r'; vz = z; ar = r• r'2;

a' = r'•+ 2r';

az = z:•

72. vr = r;

v' = r sin ';

= r• r sin

;

v = r ; ar

•

a' = r sin '•+2 sin r'+2r cos ' ; a

= r +2r r sin cos '

73. Используя формулы (2.80) и определение смешанного произ-

ведения векторов, находим

d~ey

~ez = d' [~e!

~ey ]~ez = d'

cos 1

= d'

cos 1 = !x;

cos 2

cos

cos 1

d~ez

~ex = d' [~e!

~ez ]~ex = d'

= d'

cos 2 = !y ;

cos 2

cos

d~ex

cos 1

~ey =

[~e!

~ex]~ey =

cos 2

cos 3 = !z ;

cos

откуда и следует равенство

(2.99).

75. v =

v22 + v12 2v1v2 cos

; (~v; ~v1) = arccos[(v1 v2 cos )=v]:

1ì/ñ.

76. va =p

77. va = 6ì/ñ; aa = 15:6ì/ñ2:

78. va = 0:2ì/ñ;

aa = 0:8ì/ñ2:

79. aA = 0:06ì/ñ2

; aC = 0:052ì/ñ2:

80.aa = 0:3 2ì/ñ2:

81.aa = 4:8ì/ñ2:

82.aa = 1ì/ñ2:

83.1) прямые y = 2x + c; 2) прямые y = x + c; 3) окружности

x2 + y2 = c; c > 0; 4) x2 + y2 z2 = c однополостные гиперболоиды при c > 0, двуполостные гиперболоиды при c < 0.

84. 1) grad U = 2x~ex+8y~ey +18z~ez; 2) grad U = yz~ex+xz~ey +zy~ez ; 3) grad U = exyz (yz~ex +xz~ey +zy~ez); 4) grad U = 2~r; 5) grad U = b cos br~er ; 6) grad U = ~r=r2; 7) grad U = 2(~c ~r)~c; 8) grad U = 2~r(~c ~r)2 + 2r2(~c ~r)~c;

~~ ~

9)grad U = (~c b)2~r (~r b)~c (~r ~c)b; 10) grad U = ~ez :

85.(~r ~r0) grad '(~r0) = 0; где ~r радиус-вектор произвольной

точки перпендикуляра.

86. (~r ~r0) grad '(~r0) = 0; ãäå ~r радиус-вектор произвольной точки касательной плоскости.

91. 3 R2=16.

216 Ответы и решения

96. 3=2.

99. 1)~r(t) = 0:5(t + 1)~ex + t~ey 0:5(t 3)~ez, для точки M параметр

t = 1; 2) div P = 2; 3) rot P

3~e

+ 2~e

+ ~e

101. div (r)~r = 3

+ r

;

= C=r3:

102.

, 2) 0; 3)

2~a b:

109.

4, 2) -1, 3) 2/3, 4)

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2122 / 2222

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.03.2016149.5 Кб11Б3.Б.4.4 ИЗЛ 1-й пол 19 в..doc
#
08.11.2018817.66 Кб31Банковское Дело - курс лекций.doc
#
03.05.2019729.6 Кб12Банковское дело ЛЕКЦИИ.doc
#
18.11.20183.4 Mб10Барулин В.С. - СОЦИАЛЬНАЯ ФИЛОСОФИЯ.doc
#
04.11.2018187.9 Кб12баскетбол ФГОС.doc
#
29.03.20161.13 Mб401Беляев Ю.Н. Введение в векторный анализ.pdf
#
16.11.20191.43 Mб14Беляева Теория вероятностей методичка 2006.doc
#
28.03.2016746.5 Кб26БЖД.doc
#
30.07.2019119.3 Кб1БЖД.doc
#
15.07.20193.68 Mб5Библер В.С. - ОТ НАУКОУЧЕНИЯ - К ЛОГИКЕ КУЛЬТУР....rtf
#
28.03.20169.12 Mб21Бизнес план.doc