
Беляев Ю.Н. Введение в векторный анализ
.pdf
Ÿ 9. Векторное произведение векторов |
71 |
~ |
(1.121) |
(~r ~r1) (~r2 ~r1) = 0: |
Формула (1.121) это уравнение искомой прямой в векторной форме. Используем ее для нахождения уравнения прямой линии в декартовой системе координат. Для этого раскроем векторное произведение (1.121) согласно правилу (1.120):
(y y1)(z2 (z z1)(x2 (x x1)(y2
z1) = (z z1)(y2
x1) = (x x1)(z2
y1) = (y y1)(x2
y1);
z1);
x1);
где (x; y; z) координаты вектора ~r, (x1; y1; z1) координаты вектора ~r1, (x2; y2; z2 ) координаты вектора ~r2.
Полученную систему уравнений можно переписать в эквивалентной форме
x x1 = y y1 = z z1 ; |
||
x2 x1 |
y2 y1 |
z2 z1 |
или в форме канонических уравнений прямой
x x1 |
= |
y y1 |
= |
z z1 |
; |
` |
|
m |
|
n |
|
!
где `, m, n координаты вектора M1M2.
(1.122)
(1.123)
9.3.Выражение векторного произведения через
оределители второго и третьего порядков. Если число строк матрицы, определяемой формулой (1.37), совпадает с числом е¼ столбцов, то матрица называется квадратной. Квадратной матрице M соответствует е¼ определитель, или детерминант det M , который записывается в виде той же таблицы, что и матрица M , но заключенной в прямые скобки. Так, для квадратной матрицы размерности n n имеем:
|
0 m21 |
m22 |
: : : m2n 1 |
||
|
|
m11 |
m12 |
: : : m1n |
C |
|
B .. .. |
. . . .. |
|||
M = |
B |
. . |
. |
C |
|
|
; |
||||
|
B mn1 |
mn2 |
: : : mnn C |
||
|
@ |
|
|
|
A |
det M = |
m21 |
. |
|
|
m11 |
|
.. |
|
|
|
|
|
mn1 |
|
|
|
|
|
|
m22 |
: : : |
m2n |
|
|
. |
. |
|
. |
: |
m12 |
: : : |
m1n |
|
|
.. |
|
. . |
.. |
|
|
|
|
|
|
mn2 |
: : : |
mnn |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72 |
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
Рассмотрим квадратную матрицу M , состоящую из четыр¼х элементов mij (i; j = 1; 2). Определителем или детерминантом
второго порядка, соответствующим квадратной матрице 2 2, называется число m11m22 m12m21:
|
|
m11 |
m12 |
|
|
|
|
det M |
|
|
m22 |
|
= m11m22 |
m12m21: |
(1.124) |
m21 |
|
||||||
|
|
|
|
|
|
|
|
Используя определение (1.124), формулу (1.120) для векторного произведения в ортонормированном базисе можно переписать следующим образом:
~a ~b = |
|
a2 |
a3 |
|
|
|
|
a1 |
a3 |
|
|
|
|
a1 |
a2 |
|
|
|
|
|
b3 |
|
~e1 |
|
|
|
b3 |
|
~e2 |
+ |
|
|
b2 |
|
~e3: |
(1.125) |
|
b2 |
|
b1 |
|
b1 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определитель или детерминант квадратной матрицы 3 3
åñòü
det M = |
|
m21 |
m22 |
m23 |
|
= |
|
|
m11 |
m12 |
m13 |
|
|
|
|
m31 |
m32 |
m33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
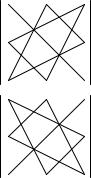
=m11m22m33 + m12m23m31 + m13m21m32
m13m22m31 m12m21m33 m11m23m32: (1.126)
a)
b)
Ðèñ. 48
Первое из тр¼х слагаемых, входящих в определение (1.126) со знаком плюс, яв-
ляется произведением элементов главной диагонали матрицы 3 3, каждое из двух
других произведением элементов, лежащих на параллели к этой диагонали, с до-
бавлением третьего множителя из проти-
воположного угла матрицы. Члены, входящие в (1.126) со знаком минус, строятся таким же образом относительно второй
диагонали. На рис. 48а схематично указано правило вычисления ½положительных\
членов определителя третьего порядка, а на рис. 48b правило вычисления его ½отрицательных\ членов.
Ÿ 9. Векторное произведение векторов |
|
|
|
|
|
73 |
||||||||||
П р и м е р 33. Ниже приведены |
результаты вычисления |
|||||||||||||||
двух определителей матрицы 3 3. |
|
|
|
|
|
|
|
|||||||||
|
|
4 3 |
1 |
|
= 10; |
|
|
2 3 |
2 |
= |
|
1: |
||||
|
|
1 |
2 |
|
|
|
|
0 |
5 |
|
|
|
||||
|
2 |
|
|
|
1 |
|
|
|
|
|||||||
2 |
3 |
5 |
|
1 |
|
2 |
0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нетрудно заметить, что векторное произведение (1.120) формально можно представить как определитель матрицы 3 3, в первой строке которой стоят базисные векторы ~e1, ~e2, ~e3, во второй строке координаты вектора ~a и в третьей строке
~
координаты вектора b :
|
|
|
|
~e1 |
~e2 |
~e3 |
|
|
|
|
|
~b = |
|
b1 |
b2 |
b3 |
|
|
|
~a |
|
|
a1 |
a2 |
a3 |
|
: |
(1.127) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задачи 60. Доказать сочетательное относительно числового множи-
|
~ |
~ |
теля свойство векторного произведения: ( ~a) b = (~a b): |
||
61. |
Доказать распределительное относительно суммы век- |
|
|
~ |
~ |
торов свойство векторного произведения: ~a (b+~c) = ~a b+~a ~c: |
||
62. |
Какими соотношениями связаны между собой единич- |
|
ные векторы левого базиса?
63. ~
Ñèëà F = 30~ex + 40~ey (Н) приложена к точке ~r = 8~ex + 6~ey (м). Найдите: 1) момент силы относительно начала координат; 2) плечо силы; 3) составляющую силы, перпендикулярную к ~r.
64. Система N частиц с массами mi, положения которых определяются радиус-векторами ~ri, а скорости ~vi, обладает моментом количества движения, равным
~
XN
K = mi(~ri ~vi):
i=1
Если же рассматривать систему координат, жестко связанную с центром масс, то можно считать, что система имеет момент
74 |
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
~
количества движения Kc. Пусть ~rc è ~vc это положение и скорость центра масс, а M сумма масс всех частиц. Покажите, что
c+ M (~rc ~vc):
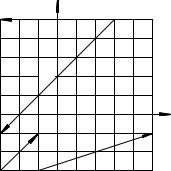
65.На масштабной сетке рис. 11 показаны десять векторов сил, лежащих в одной плоскости. Измеряя расстояния в метрах (м), силы в Ньютонах (Н) и принимая, что линейный размер ячейки сетки соответствует 1 метру для расстояний и 1 Нью-
тону для величин сил, найти сумму моментов четыр¼х сил относительно заданного на рис. 11 центра.K~ = K~
Силы, моменты которых требуется сложить, и центр, относительно которого вычисляются моменты, выбираются из таблицы согласно двузначному номеру варианта mn. Первая цифра номера m определяет векторы сил, а вторая цифра n одну из точек A, B, C, D, E, G, K, L, N , O, которую нужно использовать в качестве центра. Например, в варианте 00 требуется най-
ти сумму моментов сил |
~ |
~ |
~ |
~ |
|
|
|
|
|
|
|
|
|
|
||||||||||
F1 |
, F3 |
, F4, F9 относительно центра A. |
||||||||||||||||||||||
|
|
|
|
|
|
Т а б л и ц а к задаче 65 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
0 |
|
1 |
|
2 |
|
|
|
3 |
|
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ñ |
~ |
; |
~ |
; |
~ |
; |
|
|
~ |
; |
|
~ |
; |
~ |
; |
~ |
; |
~ |
; |
~ |
; |
~ |
; |
|
F1 |
F2 |
F3 |
|
|
F4 |
|
F5 |
F1 |
F2 |
F3 |
F4 |
F1 |
|||||||||||
|
è |
~ |
; |
~ |
; |
~ |
; |
|
|
~ |
; |
|
~ |
; |
~ |
; |
~ |
; |
~ |
; |
~ |
; |
~ |
; |
|
F3 |
F5 |
F6 |
|
|
F5 |
|
F6 |
F2 |
F3 |
F5 |
F6 |
F4 |
|||||||||||
|
ë |
~ |
; |
~ |
; |
~ |
; |
|
|
~ |
; |
|
~ |
; |
~ |
; |
~ |
; |
~ |
; |
~ |
; |
~ |
; |
|
F4 |
F8 |
F7 |
|
|
F9 |
|
F7 |
F7 |
F6 |
F8 |
F7 |
F6 |
|||||||||||
|
û |
~ |
; |
~ |
|
~ |
; |
|
~ |
|
|
~ |
; |
~ |
; |
~ |
; |
~ |
|
~ |
; |
~ |
; |
|
|
F9 |
F10; |
F8 |
F10; |
F8 |
F8 |
F9 |
F10; |
F8 |
F7 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
n |
0 |
|
1 |
|
2 |
|
|
|
3 |
|
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Центр |
A |
|
B |
|
C |
|
|
|
D |
|
|
E |
|
G |
|
K |
|
L |
|
N |
|
O |
|
П р и м е р 34. Решим задачу 65 для варианта 00. Выберем точку A за начало координат. Ось x направим по
горизонтали вправо, ось y вертикально вверх, и, соответственно, ось z перпендикулярно плоскости рис. 49.
В этой системе координат векторы сил имеют следующие компоненты:
Ÿ 9. |
Векторное произведение векторов |
75 |
||||||||
|
|
|
F1x = 2 Í; |
F1y = 2 Í; |
|
F1z = 0 Í; |
|
|||
|
|
|
F3x = 6 Í; F3y = 6 Í; F3z = 0 Í; |
|
||||||
|
|
|
F4x = 4 Í; |
F4y = 0 Í; |
|
F4z = 0 Í; |
|
|||
|
|
|
F9x = 6 Í; |
F9y = 2 Í; |
|
F9z = 0 Í; |
|
|||
а точки приложения сил |
|
|
|
|
||||||
|
|
|
|
x1 = 3 ì; y1 = 3 ì; z1 = 0 ì; |
|
|||||
|
|
|
|
x3 = 3 ì; |
y3 = 5 ì; |
z3 = 0 ì; |
|
|||
|
|
|
|
x4 = 1 ì; |
y4 = 5 ì; |
z4 = 0 ì; |
|
|||
|
|
|
|
x9 = 1 ì; y9 = 3 ì; z9 = 0 ì: |
|
|||||
|
|
|
|
y |
|
|
Момент силы |
~ |
||
|
~ |
|
|
|
|
Fi в декарто- |
||||
|
|
|
|
|
|
вой системе координат, соглас- |
||||
|
F4 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
но определению (1.113) и фор- |
|||
|
|
|
|
|
|
|
ìóëå (1.120), åñòü |
|
||
|
|
|
~ |
|
|
|
~ |
~ |
|
|
|
|
|
F3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
MA(Fi) = (xiFiz ziFiy )~ex + |
|||
|
~ |
A |
|
|
x |
|
|
+(ziFi1 xiFzi)~ey + |
||
|
F1 |
|
|
|
|
|
|
+(xiFiy yiFix)~ez : |
||
|
|
|
|
~ |
|
|
|
|
||
|
|
|
|
F9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Для рассматриваемого при- |
|||
|
|
Ðèñ. 49 |
|
|
ìåðà |
ненулевой |
будет только |
|||
|
|
|
|
проекция момента на ось z. |
||||||
|
|
|
|
|
|
|
||||
|
Вычисляем моменты при i = 1; 3; 4; 9 и складываем |
|||||||||
~ |
|
~ |
~ |
~ |
~ |
~ |
~ |
~ |
~ |
|
MA = MA(F1 ) + MA (F3) + MA |
(F4) + MA (F9) = |
|
||||||||
|
= |
|
|
(xiFiy yiFix)~ez = |
|
|
|
|||
|
i |
=1;3;4;9 |
|
|
|
|
|
|
||
|
|
X |
|
|
|
|
|
|
|
|
=( 3 2 + 3 2 3 6 + 5 6 1 0 + 5 4 1 2 + 3 6) ~ez=
=48~ez (Íì):
Модуль суммарного момента равен 38 Нм, и вектор направлен вдоль оси z перпендикулярно плоскости рисунка 49 к читателю.
76 |
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
Ÿ 10. Произведения тр¼х векторов
~
Из трех произвольных векторов ~a, b и ~c, используя операции скалярного и векторного умножения, можно образовать две
~
комбинации, имеющие смысл: смешанное произведение ~a (b ~c)
двойное векторное произведение ~
è ~a (b ~c).
10.1. ~ Смешанное произведение |
~ |
~a (b ~c) òðåõ âåê- |
торов ~a, b и ~c есть число, равное объ¼му V параллелепипеда,
построенному на привед¼нных к общему началу векторах , ~ ~a b
и ~c, взятому со знаком плюс, если угол ' между векторами ~a
è ~ острый, и со знаком минус, если угол тупой. Если b ~c '
|
|
|
|
~ |
|
|
|
|
же три вектора ~a, b, ~c компланарны, то их смешанное произ- |
||||||||
ведение равно нулю: |
|
|
|
|
||||
~a |
|
(~b |
|
~c) = |
< |
V; |
åñëè 0 ' < =2; |
(1.128) |
0; |
åñëè ' = =2: |
|||||||
|
|
8 |
V; |
åñëè =2 < ' ; |
||||
|
|
|
|
|
: |
|
|
|
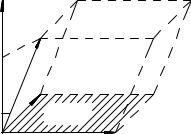
На рис. 50 показан случай, когда угол ' между векторным
~
произведением b ~c и вектором ~a меньше =2. Имеем
~ ~ ~
~a (b ~c) = ajb ~cj cos ' = jb ~cj h = Sbch = V;
ãäå Sbc площадь параллелограмма, построенного на векторах
~ |
высота параллелепипеда. |
|
b и ~c, как на сторонах; h |
||
Аналогично доказываются два других случая формулы |
||
(1.128). |
|
|
~ |
|
|
Равенство ~a (b ~c) = 0 есть необходимое и достаточное |
||
|
|
~ |
условие компланарности тр¼х векторов ~a, b и ~c. Следователь- |
||
~ |
~ |
~ |
но, любые три вектора b1 |
, b2 |
, b3 можно использовать в качестве |
базиса тр¼хмерного векторного пространства, если их смешанное произведение не равно нулю.
При циклической перестановке векторов в смешанном про-
изведении выполняются равенства |
|
|
|
~ |
~ |
~ |
(1.129) |
~a (b ~c) = b (~c ~a) = ~c (~a b): |
|||
Ÿ 10. Произведения тр¼х векторов |
77 |
|
~ |
|
|
|
b ~c |
|
|
h |
|
~a |
|
|
' |
~c |
|
|
|
|
|
|
|
~ |
|
|
|
jb ~cj |
~ |
|
|
|
|
|
|
Ðèñ. 50 |
b |
|
|
|
|
a1
~
~a (b ~c) = b1
c1
При других перестановках сомножителей в смешанном произведении оно меняет знак на противоположный.
~
Если векторы ~a, b и ~c представлены в ортонормированном базисе, то их смешанное произведение можно вычислить по формуле
a2 |
a3 |
|
|
|
c2 |
c3 |
|
|
|
b2 |
b3 |
|
; |
(1:1280) |
|
||||
|
|
|
|
|
|
|
|
|
|
в справедливости которой нетрудно убедиться, если использовать определения и свойства векторного и скалярного произведения векторов.
Ï ð è ì å ð 35. Ó ð à â í å í è å ï ë î ñ ê î ñ ò è, ï ð î õ î ä ÿ ù å é ÷ å ð å ç ò ð è ò î ÷ ê è, í å ë å æ à ù è å í à î ä í î é ï ð ÿ ì î é.
Если даны три различные не лежащие на одной прямой точ- ки M1, M2, M3, положенния которых задаются соответственно радиус-векторами ~r1(x1; y1; z1), ~r2(x2; y2; z2), ~r3(x3; y3; z3 ), то че- рез них можно провести единственную плоскость. Любая другая точка M , определяемая радиус-вектором ~r(x; y; z), будет также принадлежать этой плоскости, если три вектора (~r ~r1), (~r2 ~r1) è (~r3 ~r1) компланарны, т.е.
(~r ~r1) ((~r2 ~r1) (~r3 ~r1)) = 0;
èëè
x x1x2 x1
x3 x1
y2 |
y1 |
z2 |
z1 |
|
= 0: |
||
y |
|
y1 |
z |
|
z1 |
|
|
y3 |
|
y1 |
z3 |
|
z1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это и есть уравнения искомой плоскости в векторной форме и декартовых координатах.
78 |
Глава 1. |
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ АЛГЕБРЫ |
||
10.2. |
Двойное векторное произведение |
~ |
||
~a (b ~c). |
||||
Для него справедлива следующая формула: |
|
|||
|
~ |
~ |
~ |
(1.130) |
|
~a (b ~c) = b(~a ~c) ~c(~a b): |
|||
Простое доказательство формулы (1.130) можно получить, если применить декартовую систему координат и раскрыть покомпонентно левую и правую части этой формулы, используя определения скалярного и векторного произведений.

Глава 2
ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
Ÿ1. Производная вектор-функции по скалярному аргументу
1.1.Геометрический смысл производной. Пусть ко-
~
ординаты вектора f зависят от скалярного параметра . Тогда
~ ~
говорят, что задана вектор-функция f = f ( ) скалярного аргумента . Так, в декартовой системе координат XY Z
~
f ( ) = fx( )~ex + fy ( )~ey + fz ( )~ez :
~
Если начало вектора f ( ) для любого отнести к одной фиксированной точке O (началу координат), то при измене-
~
нии скалярного аргумента конец вектора f ( ) будет описывать некоторую пространственную кривую, называемую годо-
графом |
1 |
~ |
|
вектор-функции f ( ). |
|
~ |
|
M |
df |
|
d |
||
|
годограф
~
f ( )
M 0
~( + ) f
OÐèñ. 51
Возьмем какое-либо фиксированное значение , соответствующее определенной точке M на годографе вектор-функ-
~
ции f ( ), и зададим аргументуприращение . В результате
~
получим вектор f ( + ), определяющий на годографе некоторую точку M 0.
1Название происходит от греческого o o дорога è '! рисую. Таким образом, смысл слова - дорога, описываемая ÷åì-ëèáî. Понятие и тер-
мин введены Гамильтоном при изучении криволинейного движения частицы
79

80 Глава 2. ВЕКТОР-ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
Изменение аргумента порождает изменение вектор-функ-
~ ~ ~ ~
ции f , которое обозначим как f = f ( + ) f ( ); ему на
!0
рис. 51 соответствует вектор M M .
~
Рассмотрим отношение f приращения векторной функции к приращению скалярного аргумента. Этот вектор коллинеа-
~
рен вектору f , так как получается из последнего умножением на скалярный множитель 1= . Если при ! 0 существует предел отношения
|
~ |
~ |
|
|||
lim |
f |
= |
df |
; |
(2.1) |
|
|
|
|||||
!0 |
|
|
d |
|
||
|
|
|
|
|
|
~ |
то он называется производной вектор-функции f ( ) по скаляр- |
||||||
ному аргументу . |
|
|
|
|
|
|
При ! 0 точка M 0 приближается0 |
к точке M . Следова- |
|||||
тельно, направление секущей M M в пределе дает направление |
||||||
|
|
|
~ |
|
||
касательной, и вектор производной df направлен по касатель- |
||||||
|
|
|
|
d |
|
|
~ |
|
|
|
|
|
|
ной к годографу f ( ) в точке M . |
|
|
|
|
||
Ï ð è ì å ð 36. Ñ ê î ð î ñ ò ü è |
ó ñ ê î ð å í è å ì à ò å ð è à ë ü- |
|||||
н о й т о ч к и. Напомним, что материальной точкой (м.т.) называется тело, размерами которого в условиях данной задачи можно пренебречь и считать все его вещество сосредоточенным в одной геометрической точке.
Положение м.т. в пространстве относительно произвольно выбранного другого неизменяемого тела (или системы тел), называемого системой отсчета, задается радиусом-вектором ~r(t), зависящим от времени t и проведенным из начала системы отсчета т. O в место нахождения м.т. Годограф вектор-функции ~r(t) (линия, описываемая материальной точкой при своем движении) называтся траекторией.
Пусть за интервал времени t м.т. переместилась из положения 1, определяемого радиус-вектором ~r(t), в положение 2, определяемое радиус-вектором ~r(t + t). Изменение радиусвектора
~r = ~r(t + t) ~r(t)
это, как видно из рис. 52 и правила сложения векторов (правила треугольника), вектор, проведенный из начального положения
