4.6. Функция распределения случайной величины

Мы использовали в качестве описания д.с.в. ряд распределения. Такое описание не является единственным. Возможен и другой подход. Будем рассматривать не вероятности события для разных, а вероятности события.

Определение.Функцией распределенияслучайной величиныназывается функция, выражающая для каждоговероятность того, что случайная величинапримет значение меньше:

.

Геометрически функция распределения интерпретируется как вероятность того, что случайная точка хпопадёт левее заданной точки.

Пример 4.7.Дан ряд распределения случайной величины. Найти и изобразить графически её функцию распределения.

	1	2	3	4
	0,1	0,3	0,2	0,4

Решение. Будем задавать различные значения и находить для них:

;

;

;

;

.

Итак,

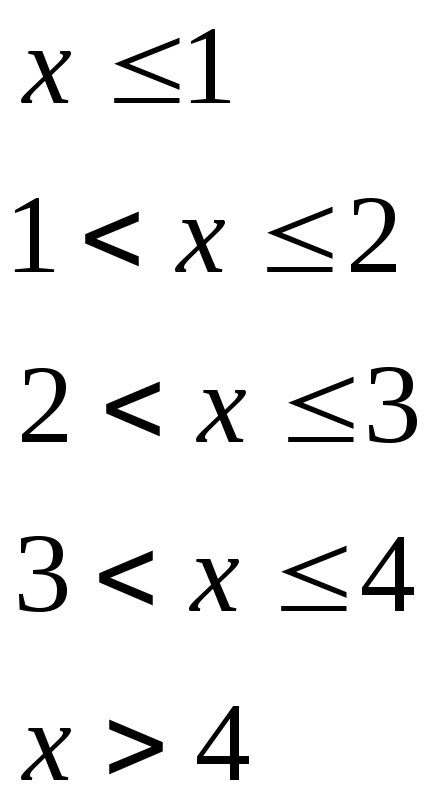
График функцииизображен на рис. 4.2.

Таким образом, функция распределения любой дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений. Сумма всех скачков функции равна единице.

Свойства функции распределения

1. ;

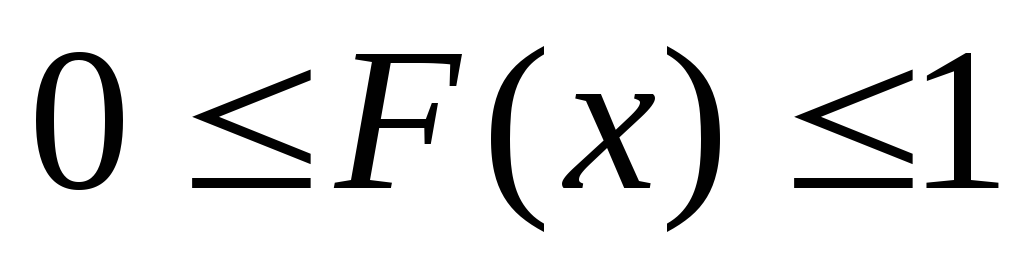2. ,

;

3. .

4. - неубывающая функция.

Пример 4.8.Функция распределения с.в.имеет вид.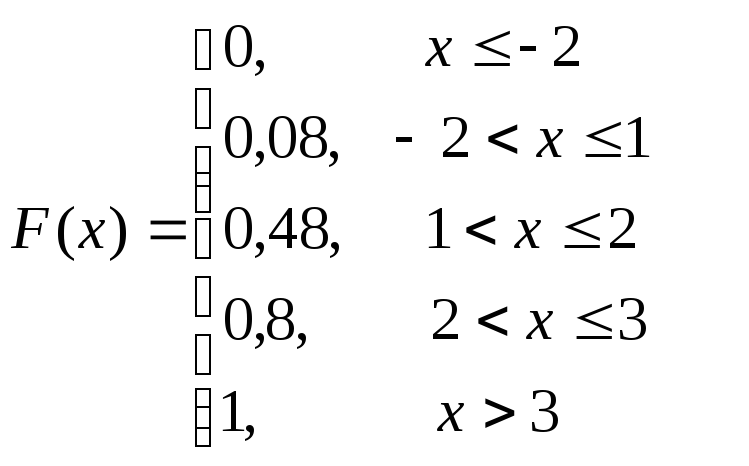

Найти вероятность того, что случайная величина примет значение в интервале .

Решение.

Тема 5. Непрерывные случайные величины.

Нормальный закон распределения

Определение.Случайная величина называетсянепрерывной, если её функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.

Теорема.Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю.

Доказательство. Представимследующим образом

.

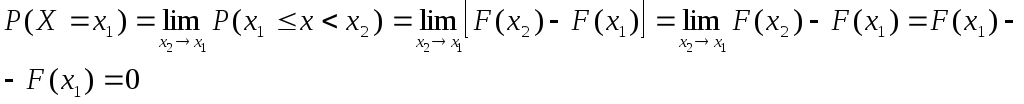Следствие. Если- непрерывная случайная величина, то вероятность попадания случайной величины в интервалне зависит от того, является этот интервал открытым или закрытым, то есть

.

5.1. Плотность распределения вероятностей непрерывных случайных величин

Непрерывную случайную величину можно задать с помощью функции распределения. Так же непрерывную случайную величину можно задавать с помощь другой функции, которая называется плотностью распределения (или плотностью вероятности, или дифференциальной функцией).

Определение.Плотностью распределениянепрерывной случайной величиныназывают функцию- первую производную от функции распределения

.

Пример 5.1.Задана функция распределения непрерывной случайной величины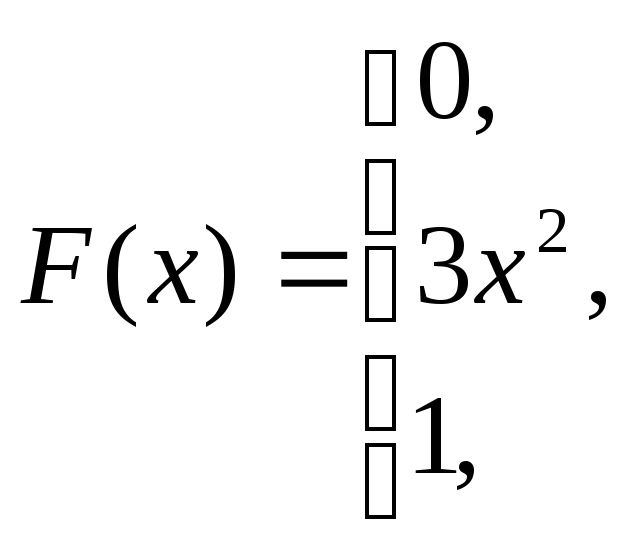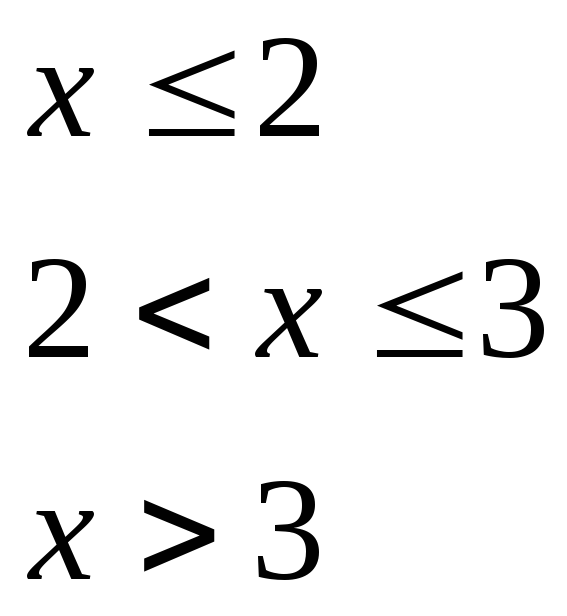. Найти плотность распределения.

Решение. По определению .

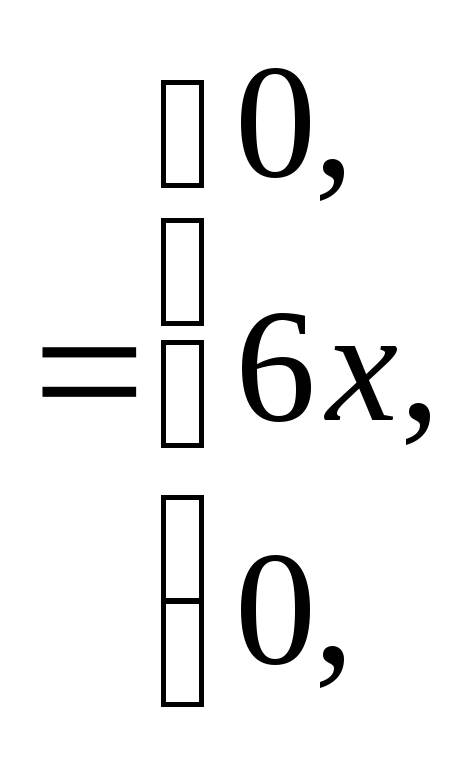
Их этого следует, что функция распределения является первообразной для плотности распределения. Зная , можно вычислить вероятность того, что случайная величина примет значение, принадлежащее заданному интервалу.

Теорема. Вероятность того, что непрерывная случайная величинапримет значение, принадлежащее интервалу, равна определенному интегралу от плотности распределения, взятому в пределах отдо:

.

Доказательство.Знаем, что. По формуле Ньютона-Лейбница. Таким образом,.

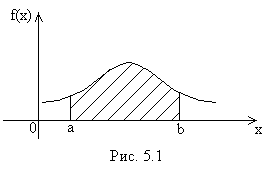
Геометрически полученный результат можно истолковать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу , равна площади криволинейной трапеции, ограниченной осью, кривой распределенияи прямыми,(рис. 5.1).

Зная , можно найти функцию распределенияпо формуле:

.

График плотности распределения называется кривой распределения.