Свойства коэффициента корреляции

1) .

2) Если и- независимые случайные величины, то.

3) Если случайные величины исвязаны линейной зависимостью, то.

6.4. Двумерный нормальный закон распределения

Определение. Случайная величинаназываетсяраспределенной по двумерному нормальному закону, если ее совместная плотность имеет вид:

,

где .

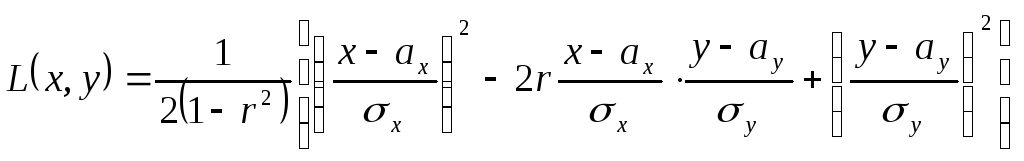Из определения следует, что двумерный нормальный закон распределения определяется пятью параметрами: .

Параметры ивыражают математические ожидания случайных величини, параметрыи- их дисперсии, а- коэффициент корреляции между случайными величинамии.

Плотности вероятности одномерных случайных величин иравны:

, .

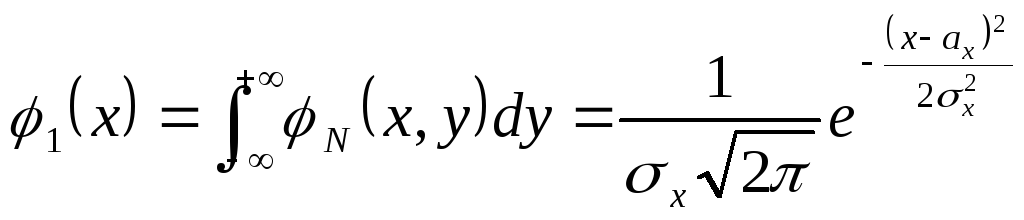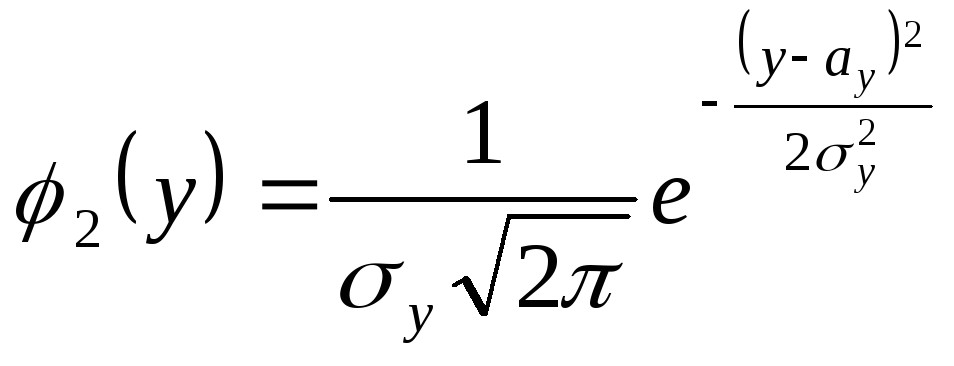Каждый из законов распределения одномерных случайных величин иявляется нормальным с параметрами соответственнои.

Найдём условные плотности вероятности случайных величин ипо формулам:

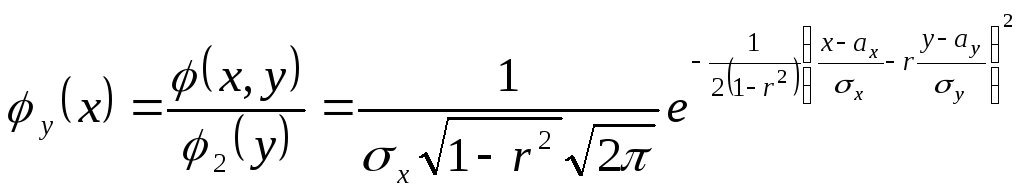и аналогично

.

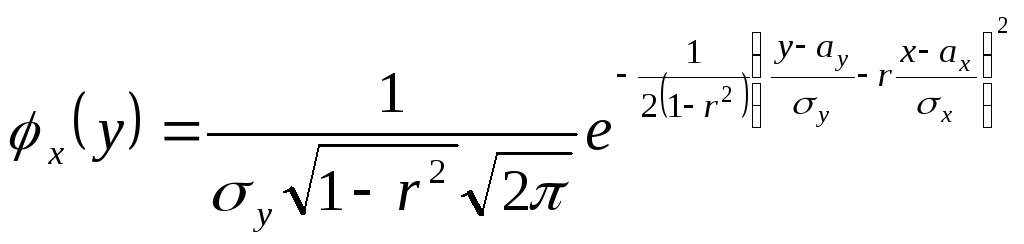Каждый из условных законов распределения случайных величин иявляется нормальным с условным математическим ожиданием и условной дисперсией, определяемыми по формулам:

, ,

, .

Из этих формул следует, что линии регрессии инормально распределенных случайных величин представляют собой прямые линии, то есть нормальные регрессиипоиповсегда линейны.

Условные дисперсии и(а значит и условные стандартные отклоненияи) постоянны и не зависят от значенийи.

Тема 7. Закон больших чисел

Известно, что нельзя заранее уверенно предвидеть, какое из возможных значений примет случайная величина в итоге испытания, - это зависит от многих причин, учесть которые невозможно. Однако оказывается, что при некоторых условиях суммарное поведение достаточно большого числа случайных величин утрачивает случайный характер и становится закономерным. Эти условия и составляют содержание закона больших чисел.

Рассмотрим неравенства Маркова и Чебышева.

1. Неравенство Маркова (лемма Чебышева)

Теорема.Если случайная величинапринимает только неотрицательные значения и имеет математическое ожидание, то для любого положительного числаверно неравенство

- неравенство Маркова.

Доказательство.Рассмотрим дискретную случайную величину. Расположим её значения в порядке возрастания. По отношению к числузначения случайной величины разбиваются на две группы: одни не больше числа, а другие больше.

I – группа II- группа

… …

Найдём математическое ожидание:

.

Так как все и по условию, то все члены правой части неотрицательны. Поэтому, если мы отбросим первыеслагаемые в выражении, получим неравенство:

.

Заменив все оставшиеся значения случайной величины меньшей величиной , получим более сильное неравенство:

или .

Сумма вероятностей – это сумма вероятностей события, то есть вероятность события.

Следовательно, .

Так как события и- противоположные, то

.

Подставляя в неравенство Маркова , получим другую формунеравенства Маркова:

.

2. Неравенство Чебышева

Теорема.Для любой случайной величины вероятность того, что отклонение случайной величины от её математического ожидания превзойдёт по абсолютной величине положительное числоне больше дроби

, - неравенство Чебышева

где .

Доказательство.Пусть- случайная величина,- её математическое ожидание. Тогда- случайная величина, которая не имеет отрицательных значений. Применим к ней неравенство Маркова, взяв за,

.

Так как неравенства иравносильны, аесть дисперсия случайной величины(по определению), то из последнего неравенства получим доказываемое неравенство:

.

Так как события и- противоположные, то

.

Подставив в неравенство Чебышева, получим другую форму неравенства Чебышева:

.

Пример 7.1.Вероятность производства нестандартной детали равна 0,1. Оценить с помощью неравенства Чебышева вероятность того, что из 10000 деталей число нестандартных окажется заключенным в границах от 950 до 1050.

Решение. Число нестандартных деталей – случайная величина , распределенная

по биноминальному закону: n= 10000,p= 0,1,q= 0,9.

Математическое ожидание и дисперсия равны:

.

Неравенство эквивалентно неравенству. Применим неравенство Чебышева прии

.

Т.е. вероятность того, что из 10000 деталей нестандартными окажется от 950 до 1050 не меньше 0,64.

Запишем неравенство Чебышева, используя вторую форму, для некоторых случайных величин.

1) Случайная величина распределена по биноминальному закону:

- число появления события в испытаниях,,.

.

2) Производится nиспытаний, в каждом из которых событие может произойти с одной и той же вероятностьюр.

- частота появления события в испытаниях,,.

.