
- •Министерство образования и науки российской федерации
- •Раздел I. Теория вероятностей
- •Тема 1. Случайные события
- •1.1 Классификация событий
- •1.2. Вероятность событий
- •Свойства вероятности
- •1.3. Элементы комбинаторики
- •1.4. Операции над событиями
- •Тема 2. Основные теоремы
- •2.1. Теорема сложения вероятностей несовместных событий
- •2.2. Теорема умножения вероятностей
- •2.3. Формула полной вероятности. Формулы Байеса
- •Тема 3. Повторные независимые испытания
- •3.1. Формула Бернулли
- •3.2. Формула Пуассона
- •3.3. Локальная теорема Муавра-Лапласа
- •Свойста функци , ее график
- •3.4. Интегральная теорема Муавра-Лапласа
- •Свойства функции :
- •Тема 4. Дискретная случайная величина и её характеристики
- •4.1. Понятие случайной величины
- •4.2. Закон распределения дискретной случайной величины
- •4.3. Математические операции над случайными величинами
- •4.4. Числовые характеристики дискретной случайной величины
- •Свойства
- •Свойства
- •4.5. Биноминальный закон распределения и закон Пуассона
- •4.6. Функция распределения случайной величины
- •Свойства функции распределения
- •Тема 5. Непрерывные случайные величины.
- •5.1. Плотность распределения вероятностей непрерывных случайных величин
- •Свойства плотности распределения
- •5.2. Числовые характеристики непрерывных случайных величин
- •5.3. Нормальный закон распределения
- •Свойства случайной величины, распределенной по нормальному закону
- •5.4. Центральная предельная теорема. Теорема Ляпунова
- •Тема 6. Двумерные (n-мерные) случайные величины
- •6.1. Способы задания двумерной случайной величины
- •Свойства двумерной функции распределения
- •6.2. Условные законы распределения
- •6.3. Ковариация и коэффициент корреляции
- •Свойства коэффициента корреляции
- •6.4. Двумерный нормальный закон распределения
- •Тема 7. Закон больших чисел
- •Неравенство Маркова (лемма Чебышева)
- •Неравенство Чебышева
- •Теорема Чебышева
- •Раздел II. Математическая статистика Тема 8. Выборочный метод. Общие вопросы
- •8.1. Понятие о вариационных рядах
- •8.2. Эмпирическая функция распределения
- •Свойства :
- •8.3. Числовые характеристики вариационного ряда
- •Основные свойства
- •Основные свойства дисперсии
- •Упрощённый способ расчёта средней арифметической и дисперсии
- •8.4. Выборочный метод
- •Тема 9. Оценка доли признака и генеральной средней
- •Точечные оценки генеральной совокупности. Свойства оценок
- •Интервальная оценка параметров
- •Доверительный интервал для генеральной средней и генеральной доли по большим выборкам
- •Объём выборки
- •Тема 10. Статистическая проверка гипотез
- •10.1. Статистическая гипотеза и общая схема её проверки
- •1) - То нулевую гипотезуотвергают,
- •2) - То нет оснований отвергнуть.
- •10.2. Построение теоретического закона распределения по опытным данным. Критерий согласия Пирсона
- •Правило проверки нулевой гипотезы
- •Тема 11. Корреляция и регрессия
- •11.1. Линейная парная регрессия
- •11.2. Оценка тесноты корреляционной зависимости
- •Свойства выборочного коэффициента корреляции r
- •Проверка значимости выборочного коэффициента корреляции
Тема 11. Корреляция и регрессия
Пусть нам требуется
установить и оценить зависимость между
случайными величинами
![]() и
и![]() .
Они могут быть связаны либо функциональной
зависимостью, либо статистической, либо
быть независимыми.
.
Они могут быть связаны либо функциональной
зависимостью, либо статистической, либо
быть независимыми.
Например, между
радиусом круга
![]() и его площадью
и его площадью![]() существуетфункциональная зависимость
существуетфункциональная зависимость![]() .
Однако на практике чаще всего встречаются
зависимые друг от друга переменные
величины, но при этом каждой из них не
соответствует определённое значение
другой. Например, связь между количеством
осадков и урожайностью имеется. Однако
известно, что количество осадков
однозначно не определяет урожайность.
Это объясняется тем, что на урожайность
влияет много других факторов. В результате
каждому значению одной величины
соответствует несколько значений другой
величины. Связи такого типа называютсястатистическими.
.
Однако на практике чаще всего встречаются
зависимые друг от друга переменные
величины, но при этом каждой из них не
соответствует определённое значение
другой. Например, связь между количеством
осадков и урожайностью имеется. Однако
известно, что количество осадков
однозначно не определяет урожайность.
Это объясняется тем, что на урожайность
влияет много других факторов. В результате
каждому значению одной величины
соответствует несколько значений другой
величины. Связи такого типа называютсястатистическими.
В частности, если при изменении одной из величин изменяется среднее значение другой, то такая зависимость называется корреляционной. Основная задача теории корреляции – выявление связи между случайными переменными и оценка её тесноты.
11.1. Линейная парная регрессия
Пусть в результате испытания получены значения случайных величин ХиY. Экспериментальные данные удобно задавать в видекорреляционной таблицы, в которой в первом столбце представлены значения с.в.Х, а в первой строке – значения с.в.Y; числа, стоящие на пересечении строк и столбцов, показывают сколько раз наблюдалась одна и та же пара чисел (xi, yj).
Рассмотрим таблицу распределения пробега автомобиля Y(вкм.) от количества израсходованного бензинаХ(вл.).
|
|
251 |
265 |
279 |
293 |
307 |
321 |
|
|
25 |
9 |
4 |
1 |
- |
- |
- |
14 |
|
27 |
1 |
10 |
9 |
3 |
- |
- |
23 |
|
29 |
- |
2 |
6 |
14 |
6 |
- |
28 |
|
31 |
- |
- |
1 |
10 |
18 |
6 |
35 |
|
|
10 |
16 |
17 |
27 |
24 |
6 |
|
В данной таблице, например, число 3 показывает, что пара (27, 293) наблюдалась три раза, т.е. 3 автомобиля израсходовали 27 л. бензина и при этом их пробег составил 293км. Прочерк ” - ” означает, что пара не наблюдалась. В последней строке (столбце) указана сумма чисел, расположенных во внутренних клетках по столбцам (строкам).
Символами
![]() будем
обозначать числа во внутренних клетках,
будем
обозначать числа во внутренних клетках,![]() -
количество (частота) автомобилей
израсходовавших
-
количество (частота) автомобилей
израсходовавших![]() л.
бензина,
л.
бензина,
![]() -
количество (частота) автомобилей, пробег
которых составляет
-
количество (частота) автомобилей, пробег
которых составляет![]() км.
км.
В нижнем правом углу
указана сумма всех частот
![]() .
.
Замечание. В
случае интервального статистического
распределения с.в.![]() и
и![]() в качестве
в качестве![]() ,
,![]() выбирают середины интервалов;
выбирают середины интервалов;![]() ,
,![]() - частоты попадания случайной величины
в данные интервалы.
- частоты попадания случайной величины
в данные интервалы.
Корреляционная
таблица показывает, что с увеличением
объема израсходованного бензина Хпробег автомобиля![]() имеет тенденцию к повышению. Для более
точного рассмотрения этой закономерности
рассмотримгрупповые средние:
имеет тенденцию к повышению. Для более
точного рассмотрения этой закономерности
рассмотримгрупповые средние:
 и
и
 .
.
Вычислим групповые средние для нашего распределения.
![]()
![]() .
.
![]()
![]()
![]()
![]()
Результаты вычислений поместим в таблице:
-
у
251
265
279
293
307
321

25,2
26,75
27,82
29,52
30,5
31
![]()
![]()
![]()
![]()
Результаты вычислений поместим в таблице:
-
х
25
27
29
31

257
273,52
291
304,6
На рис. 11.1 построим
графики ломаных, соединив точки с
координатами
![]() и
и![]() .
.

Определение.
Эмпирической линией регрессии
![]() по
по![]() называется ломаная, соединяющая точки
с координатами
называется ломаная, соединяющая точки
с координатами![]() .Эмпирической линией регрессии
.Эмпирической линией регрессии
![]() по
по![]() называется ломаная, соединяющая точки
с координатами
называется ломаная, соединяющая точки
с координатами![]() .
.
По виду ломаных
(рис. 11.1) можно предположить наличие
линейной корреляционной зависимости
![]() по
по![]() (ломаная 1) и
(ломаная 1) и![]() по
по![]() (ломаная 2) между рассматриваемыми
переменными.
(ломаная 2) между рассматриваемыми
переменными.
Поставим задачу найти уравнения этих линий называемые теоретическими линиями регрессии.
Будем искать уравнение
регрессии
![]() по
по![]() в виде
в виде
![]() .
(11.1)
.
(11.1)
Неизвестные параметры
![]() и
и![]() выберем таким образом, чтобы сумма
квадратов отклонений эмпирических
групповых средних
выберем таким образом, чтобы сумма
квадратов отклонений эмпирических
групповых средних![]() от значений
от значений![]() ,
найденных по уравнению (11.1)
,
найденных по уравнению (11.1)![]() ,
была минимальной.
,
была минимальной.
Исследуем функцию![]() на
минимум.
на
минимум.
Т.к. функция
![]() является функцией двух переменных, то
необходимым условием существования
экстремума является равенство нулю
частных производных:
является функцией двух переменных, то
необходимым условием существования
экстремума является равенство нулю
частных производных:
![]() .
.
Вычислим частные производные и приравняем их нулю:

Преобразовав и разделив каждое уравнение системы на n, получим
систему нормальных
уравнений: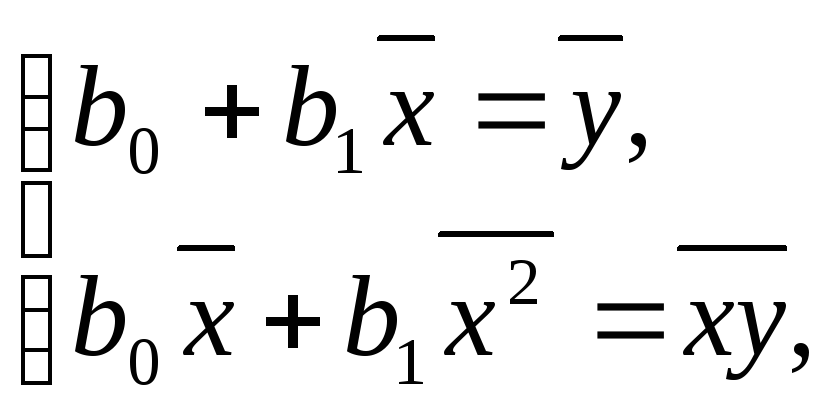
![]()
где
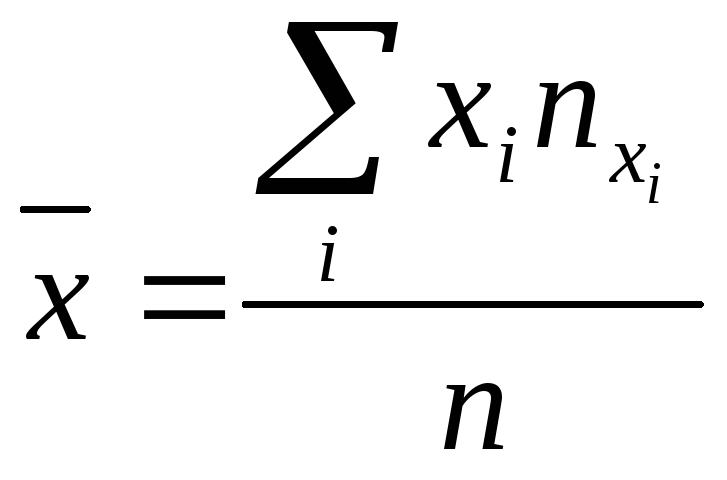 ,
, ,
, ,
, .
.
Решив эту систему, найдем искомые параметры:
![]() ,
,
![]() .
.
Определение.Угловой коэффициент![]() прямой линии регрессии
прямой линии регрессии![]() по
по![]() называюткоэффициентомрегрессии
называюткоэффициентомрегрессии![]() по
по![]() и обозначают
и обозначают![]() :
:
![]() .
.
Числитель
![]() :
:![]() - называетсявыборочной ковариацией.
- называетсявыборочной ковариацией.
Знаменатель
![]() :
:![]() - называетсявыборочной дисперсией
- называетсявыборочной дисперсией![]() .
.
Т.о. теоретическая
линия регрессии
![]() по
по![]() имеет вид:
имеет вид:![]() .
(11.2)
.
(11.2)
