Решение второй задачи

Решающим положением для неё будет, когда плоскость (ABC) станет параллельной новой плоскости проекций. Для этого вначале чертёж нужно преобразовать так, чтобы плоскость заняла бы положение проецирующей относительно новой плоскости проекций . Это было сделано при решении первой задачи.

Далее, проводим новую плоскость проекций: ; ||. Расстояния всех точек на плоскости проекций до плоскости берём с плоскости проекций . При этом проекция АВС является истинной величиной треугольной грани АВС и определяет её площадь.

Вопросы для самоконтроля

1. В чём принцип преобразования чертежа методом вращения заданной геометрической фигуры вокруг проецирующей оси?

2. В чём принцип преобразования чертежа методом вращения заданной геометрической фигуры вокруг прямой уровня?

3. В чём принцип преобразования чертежа методом введения дополнительных плоскостей проекций?

4. Какие решающие положения можно получить для прямых линий общего положения, преобразуя чертёж, какие задачи при этом становятся решёнными?

5. Какие решающие положения можно получить для плоскостей общего положения, преобразуя чертёж, какие задачи при этом становятся решёнными?

8. Конструктивные задачи графического моделирования

Конструктивными называют задачи, связанные с конструированием геометрических фигур, их взаимного положения, а так же взаимного положения их элементов по заданным условиям. Эти задачи являются, обычно, разновидностью комплексных, включая в себя, как правило, несколько позиционных и метрических задач. Решение конструктивных задач связано с реализацией на чертеже заданных геометрических условий. При описании геометрических условий и решений конструктивных задач геометрические фигуры (линии и поверхности) удобно моделировать, как множество точек или множество прямых, отвечающих заданным условиям.

8.1. Примеры конструктивных задач

со множеством точек (ВМТ)

Пример 1 (рис. 8.1). Построить на заданной плоскости всё множество точек (ВМТ), равноудалённых от заданной на ней точки O.

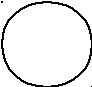
Решение

Это окружность m на заданной плоскости с центром в точкеО.

Пример 2 (рис. 8.2). Построить ВМТ, равноудалённых от заданной пространственной точки О.

Решение

Это сфера с центром в т. О.

Om=

Om

Рис. 8.1

O

O

Рис. 8.2

Пример 3 (рис 8.3). Построить ВМТ, равноудалённых от заданной прямой i .

Решение

Это цилиндр вращения с осью i .

i

i

Рис. 8.3

Пример 4 (рис. 8.4). Построить ВМТ, равноудалённых от двух заданных точек А и В.

Решение

Это плоскость , проходящая перпендикулярно отрезку АВ через его середину (точку М).

B

M

A

A M B

Рис. 8.4

Пример 5 (рис. 8.5). Построить прямую a, все точки которой были бы равноудалены от заданных точек А и В, при этом прямая a должна быть параллельной плоскости .

Решение

Прямая а расположена в плоскости предыдущего примера. Она перпендикулярна отрезку АВ.

a=B

M= K

A

A M B

a K

Рис. 8.5

Пример 6 (рис. 8.6). Построить ВМТ, равноудалённых от двух заданных пересекающихся плоскостей: и .

Решение

Это две биссекторные плоскости: и .

Рис. 8.6

8.2. Примеры конструктивных задач

со множеством прямых линий (ВМП)

Пример 1 (рис.8.7). Построить всё множество прямых (ВМП), проходящих через заданную точку A перпендикулярно заданной прямой b .

Решение

Это плоскость (hf), проходящая через заданную точку А перпендикулярно прямой b .

Ahb

f

h

f

Afb

Рис. 8.7

Пример 2 (рис. 8.8). Даны скрещивающиеся прямые линии: а и b. Построить ВМП, пересекающих прямую a и параллельных прямой b.

Решение

Это плоскость (ca), проходящая через прямую a параллельно прямой b .

с|| b a

b

c|| b

a

b

Рис. 8.8

Пример 3(рис. 8.9). ПостроитьВМП, равноудалённых от заданной прямойа.

Решение

Это цилиндр вращения, у которого заданная прямая а – ось вращения.

a

a

Рис. 8.9

Пример 4(рис. 8.10). ПостроитьВМП, проходящих через заданную т.А и пересекающих заданную плоскостьпод одинаковым углом.

Решение

Это конус вращения , у которого ось i расположена перпендикулярно заданной плоскости .

A

i

i= A

Рис. 8.10

Пример 5 (рис. 8.11). Построить ВМП, равнонаклонённых к пересекающимся плоскостям и .

Решение

Это биссекторные и перпендикулярные им плоскости и .

Рис. 8.11

Пример 6. Определить геометрическую фигуру, представляющую собой ВМП, скрещивающихся с заданной прямой i под одинаковым углом и равноотстоящих от неё.

Решение

Это однополостный гиперболоид вращения с осью вращения i .

8.3. Примеры решения конструктивных задач

Пример 1 (рис. 8.12). Построить ВМТ, равноудалённых от двух заданных параллельных прямых а и b.

Решение

Это плоскость , проходящая через середину их общего перпендикуляра и перпендикулярно ему (параллельно прямым а и b).

a

b

b

b

a

a

Рис. 8.12

Пример 2 (рис. 8.13). В заданной грани АВС построить ВМТ, равноудалённых от заданных точек М и К, расположенных вне плоскости (АВС).

Решение

Это прямая m – результат пересечения плоскости (АВС) плоскостью , проходящей через середину отрезка МК перпендикулярно ему.

Пример 3 (рис. 8.14). В плоскости (А, b) через точку А провести прямую l под углом к плоскости проекций .

Решение

Всё множество прямых l, которые проходят через точку А под углом к плоскости , есть конус вращения , у которого A i , угол ( l ) = . Искомая прямая – одна из двух образующих l, являющихся результатом пересечения этого конуса с плоскостью (A, b).

BM

m

ACK

C

AM= K

m

B

Рис. 8.13

b

A

h

i

ll

h

b

A

hh||hll

Рис. 8.14

Пример 4 (рис. 8.15). Построить ВМП, проходящих через заданную точку М и касательных к заданной сфере .