
Лекции по алгебре.Баскаков
.pdf
7
ГЛАВА 1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
Некоторые обозначения и соглашения
Под множеством понимается совокупность некоторых объектов, объединенных общим признаком. Примеры: 1) множество жителей города Воронежа; 2) множество точек плоскости; 3) множество треугольников плоскости; 4) множество N натуральных чисел; 5) множество Z целых чисел; 6) множество Q рациональных чисел; 7) множество R вещественных чисел. Структура объектов, входящих в данное множество, не рассматривается при изучении этого множества.
В 1872 г Георг Кантор, основатель теории множеств, определил множество как "объединение в одно целое объектов, хорошо различимых нашей интуицией или нашей мыслью".
Множества обычно обозначают большими буквами X; Y; Z; A; B; C; : Объекты, входящие в данное множество X; называются его элементами; они обозначаются малыми буквами x; y; z; a; b; c; ::: : Запись x 2 X означает, что x является элементом множества X , а запись x2X или x 2= X означает, что элемент x не принадлежит множеству X:
Если множество A состоит из элементов, принадлежащих множеству X , то говорят, что A является подмножеством множества X (или A включено в X ), и в этом случае пишут A X (или A X ). Например, Z – подмножество множества R (кроме того, N Z Q R). Используется также обозначение X A, которое читается так: X содержит A. Два множества X и Y называются равными, если одновременно X Y и Y X; т.е. они состоят из одних и тех же элементов.
Для описания множества пользуются двумя способами. Первый состоит в простом перечислении его элементов. Так, например, запись A = f0; 1; 5g означает, что множество A состоит из трех чисел 0, 1 и 5. Второй способ состоит в определении множества с помощью некоторого свойства P , позволяющего определить принадлежит ли данный элемент данному множеству или нет. В этом случае используется коллективизирующее обозначение
A = fx : P (x)g;
которое читается следующим образом: множество A состоит из всех элементов x, для которых P (x) истинно. Если свойство P относится к элементам некоторого множества X , то будем писать также A = fx 2 X : P (x)g. Например, множество f1; 2; 3; 4; 5g можно задать следующим образом:
8 |
Глава 1. Элементы теории множеств |
f1; 2; 3; 4; 5g |
= fx : x – целое число, удовлетворяющее неравенству |
1 x 5g = fx 2 Z : 1 z 5g: Аналогичным образом могут быть заданы следующие множества
[a; b] = fx 2 R : a x bg; (a; b) = fx 2 R : a < x < bg:
Часто используется множество, которое называется пустым и обозначается символом ;: По определению ; = fx : x 6= xg: Поскольку нет элементов, удовлетворяющих условию x 6= x; то ; не содержит элементов. Ясно, что
;A для любого множества A.
x 1. Операции над множествами
Рассмотрим задачу построения новых множеств из тех, которыми мы располагаем.
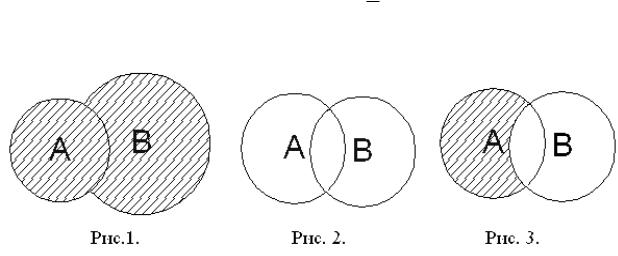
Определение 1. Объединением двух множеств A и B называется множество (см.рис. 1)
[
AB = fx : x 2 A ; x 2 Bg:
Определение 2. Пересечением двух множеств A и B называется множество (см.рис.2)
\
AB = fx : x 2 A ; x 2 Bg:
Определение 3. Разностью двух множеств A и B называется множество (см.рис.3)
A n B = fx 2 A : x2Bg:
Определение 4. Если A – подмножество множества X , то множество X n A называют дополнением множества A до множества X и обозначают также символом A0 или CA:

x 1. Операции над множествами |
9 |
Определение 5. Симметрической разностью двух множеств A и B
называется множество
[
A B = (AnB) (BnA):
Аналогично определяется объединение и пересечение любого (конечного или бесконечного) числа множеств A ; 2 I; где I – некоторое множество индексов. А именно, положим
[
A = fx : x 2 A хотя бы для одного 2 Ig;
2I
\
A = fx : x 2 A для всех 2 Ig:
2I
Отметим следующие свойства введенных операций над множествами |
|
1) A (B C) = (A B) C; |
|
2) A S(B SC) = (A SB) SC; |
|
3) A T(B TC) = (A TB) T(A C); |
|
4) A S(B TC) = (A SB) T(A SC); |
|
T S |
T S T |
5)(A SB)0 = A0 TB0;
6)(A TB)0 = A0 SB0:
ST
7) (A B) = (A B)n(A B);
8)(A B) C = A (B C);
9)(A B) C = (A SB SC)n(A TB TC):
Последние два свойства относятся к множествам A; B, являющимся подмно-
жествами некоторого множества X . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Докажем шестое свойство. По определению равных множеств нам следу- |
|||||||||||||||||||||||||||||||
ет доказать включения (A |
T |
B)0 |
= Xn(A |
T |
B) A0 |
S |
B0 |
= (XnA) |
S |
(XnB) и |
||||||||||||||||||||||
A0 |
S |
|
|
T |
|
: |
Для |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
||||||||||
|
|
|
|
|
2 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
B0 |
|
|
(A B)0 |
|
|
|
доказательства первого включения рассмотрим про- |
|||||||||||||||||||||||||
извольный элемент x |
|
|
X |
|
(A |
B): Это означает, что x |
|
X , но x |
A B, |
|||||||||||||||||||||||
то есть |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
B |
. Отсюда следует, что |
x принад- |
|||||||||||
|
|
не принадлежит либоT , либо |
|
|
|
|
T |
|||||||||||||||||||||||||
лежит либо X n A; либо X n B, и поэтому x 2 A0 |
|
B0: Таким образом, |
||||||||||||||||||||||||||||||
|
T |
|
|
|
A0 |
S |
B0 |
|
|
|
|
|
|
|
|
x |
|
A0 |
S |
|
|
|
|
2 |
|
|
n |
|
||||
(A B)0 |
|
|
|
. Обратно, если |
2 |
|
B0; |
то |
x принадлежит хотя бы |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
||||||||||||
одному из множеств A0; B0: Для определенности пусть x |
|
A0 = X A. Это |
||||||||||||||||||||||||||||||
(A |
B): Итак, |
A0 |
|
|
B0 |
(A B)0: T |
|
|
|
|
|
|
|
|
|
|
T |
|
|
|||||||||||||
означает, что x |
2A; и поэтому x2A |
|
B. Следовательно, x 2 (A |
B)0 = X n |
||||||||||||||||||||||||||||
|
TМножество, |
состоящее из двух элементов и в котором определен поря- |
||||||||||||||||||||||||||||||
|
|
S |
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
док следования элементов, называется упорядоченной парой. Для записи упорядоченной пары используются круглые скобки. Так запись (a; b) означает двухэлементное множество, в котором элемент a считается первым, а элемент b вторым. Две упорядоченные пары (a; b) и (b; a) при a 6= b считаются
10 |
Глава 1. Элементы теории множеств |
различными, хотя двухэлементные множества fa; bg и fb; ag одинаковы (совпадают). Аналогичным образом дается определение упорядоченного набора из n элементов.
Определение 5. Пусть X1 и X2 – два непустых множества. Произведением (или декартовым произведением) этих множеств будем называть множество упорядоченных пар (x1; x2), где x1 2 X1 и x2 2 X2 , т.е.
X1 X2 = f(x1; x2) : x1 2 X1; x2 2 X2g:
Это понятие выросло из понятия декартовой системы координат на плоскости.
Определение произведения двух множеств естественно обобщается на случай n множеств. Если X1; X2; : : : ; Xn – n непустых множеств, то их (декартово) произведение X1 Xn состоит из всевозможных упорядоченных наборов (x1; : : : ; xn); xk 2 Xk; k = 1; :::; n элементов этих множеств.
Если все множества X1; :::; Xn совпадают: X1 = X2 = ::: = Xn = X; то их проведение X1 ::: Xn обозначается Xn . Так, например, символом Rn обозначается множество упорядоченных наборов n вещественных чисел.
x 2. Отношения эквивалентности. Фактор-множества
По данному множеству X можно строить новые множества, рассматривая множество некоторых подмножеств множества X . Следует сказать, что принято говорить не о множестве подмножеств данного множества, а о классе подмножеств или семействе подмножеств. Так, например, класс всех подмножеств множества X = f1; 2; 3g состоит из подмножеств ;; f1g; f2g; f3g; f1; 2g; f1; 3g; f2; 3g; f1; 2; 3g: Таким образом, элементами вновь построенного множества могут быть подмножества данного множества.
В самых различных вопросах (примеры будут приведены) приходится рассматривать класс таких подмножеств данного множества X , которые взаимно не пересекаются и объединение этих подмножеств совпадает с X . Например, плоскость можно представить как объединение прямых, параллельных данной прямой. Физическое пространство есть объединение концентрических сфер (начиная со сферы радиуса нуль). Множество жителей города Воронежа можно разбить на группы по их году рождения. В биологии все множество животных разбивается на типы, типы - на классы и т.д.
Если данное множество X можно представить в виде объединения своих попарно непересекающихся подмножеств, то будем говорить, что X разбито на классы.
x 2. Отношения эквивалентности. Фактор-множества |
11 |
Разбиение данного множества на классы осуществляется на базе того или иного признака (это мы видим на примерах), по которому элементы множества X объединяются в классы. Чтобы придать этому высказыванию более точный смысл, введем несколько понятий.
Определение 1. Пусть X – непустое множество. Подмножество R из произведения X X называется бинарным отношением на множестве X . Если пара (x; y) входит в R, иногда будем писать xRy и говорить, что элемент x находится в отношении R с y:
Так, например, отношения x = y; x y; x < y; x2 + y2 = 1; x 6= 0 являются бинарными отношениями на R.
Определение 2. Бинарное отношение R на X называется отношением эквивалентности, если оно обладает следующими тремя свойствами:
а) рефлексивность: (x; x) 2 R 8x 2 X; |
|
б) симметричность: из (x; y) 2 R следует, что (y; x) 2 R; |
|
в) транзитивность: если (x; y) 2 R |
и (y; z) 2 R; то (x; z) 2 R: |
Вместо того, чтобы писать (x; y) |
2 R, пишут x y или, еще короче, |
x y (если ясно, о каком отношении идет речь). Элементы x и y будем называть эквивалентными.
Из четырех бинарных отношений на R, рассмотренных после определения 1, отношением эквивалентности является только первое. Рассмотрим другие отношения эквивалентности.
Пример 1. Рассмотрим множество Z целых чисел. Пусть X - подмножество из Z Z; состоящее из пар вида (p; q); где q 6= 0: Отношение эквива-
лентности R на X зададим формулой (p; q) (p0; q0); если pq0 = p0q: Таким образом, R = f((p; q); (p0; q0)) : (p; q) (p0; q0)g:
Пример 2. Пусть Z - множество целых чисел и m 1 - некоторое целое число. Отношение эквивалентности R на Z определим так, чтобы p q в точности тогда, когда число p q делится на m: Итак, R = f(p; q) 2 Z Z : p qg:
Пример 3. Пусть X – множество прямых на плоскости (или в простран-
стве). Определим отношение эквивалентности на |
X следующим |
образом: A B, если прямые A и B параллельны или совпадают. |
|
Пример 4. Рассмотрим множество Y , всех направленных отрезков про- |
|
~ |
~ |
странства (плоскости). Два направленных отрезка AB и CD называются
эквивалентными, если они имеют одинаковую длину, лежат на параллельных прямых и одинаково направлены. Так, введенное бинарное отношение (множество пар эквивалентных направленных отрезков) является отношением эквивалентности.
Другие важные примеры отношений эквивалентности будут рассмотре-

12 Глава 1. Элементы теории множеств
ны несколько позже.
Далее символом X обозначается множество, на котором задано отношение эквивалентности R.
Определение 3. Подмножество A из X называется классом эквивалентности, если 1) оно состоит из эквивалентных друг другу элементов и 2) если x 2 X эквивалентен хотя бы одному элементу из A, то x 2 A:
Т е о р е м а. Два класса эквивалентности либо совпадают, либо не пересекаются.
Доказательство. Пусть A и B – два класса эквивалентности из X .
Допустим, что они пересекаются и x 2 A |
B. Если a – некоторый элемент |
|||||||
из A, то a x: Поскольку x 2 |
a |
2 |
B |
. Таким образом, |
A |
|
B |
. |
B, то и T |
|
|
|
|||||
Аналогично доказывается, что B A. Итак, A = B. Теорема доказана.
Из свойства транзитивности отношения эквивалентности следует, что класс эквивалентности является множеством всех элементов, эквивалентных произвольному элементу из этого класса. Таким образом, из теоремы следует, что отношение эквивалентности позволяет данное множество X представить в виде объединения взаимно непересекающихся классов эквивалентности.
Определение 4. Совокупность всех классов эквивалентности называется фактор-множеством. Оно обозначается символом X=R:
Как уже отмечалось, каждый элемент x из множества X полностью определяет класс эквивалентности его содержащий, который далее обозначается символом x~, так что x 2 x~ (и x~ = y~ если и только если x y). Элемент x называется представителем класса A, если x 2 A.
Теперь вернемся к рассмотрению примеров 1 – 3 отношений эквивалентности и найдем соответствующие фактор-множества.
В первом примере фактор-множество совпадает с множеством Q рациональных чисел, так как рациональное число определяется как совокупность пар (p; q); q 6= 0; где при pq0 p0q = 0 две пары (p; q) и (p0; q0) определяют одно и то же рациональное число.
Во втором примере фактор-множеством являются множества целых чи-
сел, сравнимых по модулю m. Это множество состоит из элементов
~ |
~ |
= f2 + km : k 2 Zg; :::; m~ = fkm : k 2 Zg: |
1 = f1 + km : k 2 Zg; 2 |
||
Например, при m = 2 оно состоит из двух классов: четных чисел и нечетных чисел.
В третьем примере фактор-множество есть множество направлений прямых на плоскости (пространства). Каждая из параллельных друг другу прямых (из класса эквивалентности) служит "представителем"направления (на-

x 2. Отношения эквивалентности. Фактор-множества |
13 |
правление на плоскости или в пространстве есть множество всех параллельных лучей плоскости или пространства).
Наконец, в четвертом примере фактор-множество состоит из свободных векторов (свободный вектор – подмножество направленных отрезков пространства, имеющих одинаковую длину, лежащих на параллельных прямых и одинаково направленных, т.е. является классом эквивалентности).
Множество свободных векторов пространства обозначим через V 3 (а плоскости через V 2 ).
Множество Z целых чисел можно определить как фактор-множество
следующим образом. На множестве X = N N введем отношение эквивалентности: (m; n) (p; q); если m+q = n+p: Класс эквивалентности, состоящий из пар вида (n; n); n 1; называется нулевым числом.
Взаключение параграфа договоримся об использовании некоторых логических символов.
Импликация. Скажем, что предложение P влечет (имплицирует) предложение Q, если Q справедливо всякий раз, когда справедливо P . В этом случае используется запись P ) Q: Предложения P и Q называются эквивалентными, если одновременно P ) Q и Q ) P ; это записывается следующим образом P , Q (свойство Q есть необходимое и достаточное условие для того, чтобы имело место свойство P ).
Кванторы. Символы 8 и 9 называются кванторами. В данном учебном пособии символ 8 обозначает выражение "каково бы ни было"или "для любого а символ 9 обозначает выражение "существует".
Равенство. Равенство обозначается символом = и имеет в математике многообразный смысл.
1. Равенство означает тождество. Равенство x = y означает, что x и y не различаются. Например, пишут 1 = 1.
2. Равенство может быть условным; такой смысл имеет равенство между двумя частями уравнения. Например, равенство ax = b означает, что это равенство имеет место только тогда, когда x принимает конкретное значение.
3. Знак равенства ставится между элементами одного класса эквивалентности из фактор-множества. Например, вместо записи 2/3 4/9 (см. пример
1)используется запись 2/3 = 4/6 .
Вдальнейшем нами часто используется метод математической индук-
ции.
Пусть P (n) - некоторое утверждение, зависящее от n 2 N; n n0: Метод математической индукции описывается следующим образом:
1) проверяется справедливость утверждения P (n0)(база индукции),
2) предполагается, что утверждение P (n) справедливо для всех n < k;

14 Глава 1. Элементы теории множеств
где k > n0 (индукционное предположение),
3) доказывается, что утверждение P (n) верно для n = k (индукционный переход).
Если все три этапа проделаны, то утверждение P (n) верно для всех n n0: В этом и состоит принцип математической индукции. Говорят также, что утверждение доказано методом математической индукции.
Определение 5. Бинарное отношение R на множестве X называется отношением порядка на X (для пары (x; y) 2 R используется обозначение x y, причем, пишут x < y для x 6= y;) если выполнены свойства:
1)x x 8x 2 X;
2)если x y и y x одновременно, то x = y;
3)из условий x y; y z следует, что x z:
Множество X , на котором введено отношение порядка, называется частично упорядоченным множеством. Подмножество S из x называется линейно упорядоченным, если для любой пары a; b различных элементов из S либо a < b; либо b < a:
Множество Rn будет являться частично упорядоченным множеством, если положить x y; для x = (x1; : : : ; xn); y = (y1; : : : yn); удовлетворяющих условию xi yi; 1 i n:
Множество S(X) всевозможных подмножество (непустого) множества X является частично упорядоченным множеством, если отношение порядка ввести таким образом: A B; для A B:
Упражнения к §§ 1,2
1.Докажите равенства 1) - 5) из x 1.
2.Пусть A ; 2 I – некоторая совокупность подмножеств из множества
X , индексированная элементами множества I . Докажите равенства
[ |
\ |
\ |
[ |
Xn( |
A ) = |
(XnA ); Xn( A ) = |
(XnA ): |
2I |
2I |
2I |
2I |
3.Докажите, что бинарные отношения, определенные в примерах 1-3, являются отношениями эквивалентности.
4.Рассмотрим множество R вещественных чисел и рассмотрим бинарное отношение: x y, если x y – целое число. Докажите, что это отношение эквивалентности и найдите соответствующее фактор-множество.
5. На множестве R введено бинарное отношение F = f(x; y) 2 R2 : jx yj 1g: Будет ли оно отношением эквивалентности?
x 3: Отображения множеств и классификация отображений |
15 |
6.На плоскости P выбрана некоторая декартова прямоугольная система координат. На P заданы три бинарных отношения: A B для A; B 2 P , если их координаты (a1; a2); (b1; b2) удовлетворяют соответствующему условию
1)a1 = b1; a2 b2 2 Z;
2)a1 b1; a2 b2 2 Z;
3)a1 b1 + a2 b2 2 Z:
Докажите, что отношения 1)-3) являются отношениями эквивалентности. Найдите соответствующие фактор-множества.
x 3. Отображения множеств и классификация отображений
Одним из важнейших широко используемых в современной математике понятий является понятие отображения множеств.
Определение 1. Пусть X и Y – два непустых множества. Отображением f множества X называется правило, по которому каждому элементу из X ставится в соответствие вполне определенный элемент из множества
Y .
В этом случае для записи отображения используется запись f : X ! Y
или X f! Y (используется также обозначение x 7!f(x)): Символом f(x) обозначается элемент y 2 Y , который ставится в соответствие элементу x 2 X и называется значением отображения f на элементе x.
Множество X называют областью определения отображения f , а множество Y – областью значений.
Отображения множеств называют также функциями, преобразованиями, операторами. Например, отображение f : X ! Y обычно называют функцией, если X и Y – подмножества из R (т.е. числовые множества), либо таким является одно из них.
Особо отметим, что следует различать отображение f и элемент f(x), равный значению отображения f на элементе x. Однако это различие иногда не принимается во внимание. Так, например, неправильно (но удобно) говорить "функция cos x хотя следовало бы читать "функция cos".
Важно отметить еще, что отображение f считается заданным, если заданы как его область определения X , так и область значений Y: Таким образом, отображение есть тройка (X; Y; f).
Пример 1. Функция f , определенная формулой f(x) = 1=x; является отображением множества Rnf0g отличных от нуля вещественных чисел

16 Глава 1. Элементы теории множеств
в Rnf0g: Можно также рассматривать отображение g : R+ ! R+(R+ = ft 2 R : t > 0g – множество положительных чисел), определенное с помощью формулы g(x) = 1=x; x > 0: Эта функция g отличается от функции f , так как они имеют разные области определения.
В школьном курсе математики рассматриваются другие примеры функций.
Пример 2. Пусть E – множество отрезков из R: Каждому отрезку [a; b] поставим в соответствие его длину b a: Получим отображение : E ! R.
Пример 3. Пусть B – множество жителей города Воронежа и S – множество слов. Каждому жителю сопоставим его имя. Получим отображение из множества B в множество S .
Пример 4. Пусть X – непустое множество и R отношение эквивалентности на X . Каждому элементу x из X поставим в соответствие класс экви-
валентности |
x;~ |
его содержащий. Тем самым получили |
отображение |
f : X ! X=R. |
|
Пусть X – произвольное множество. |
Отображение |
Пример |
5. |
IX : X ! X (обозначаемое также символом I , если ясно, о каком множестве идет речь), определенное равенством IXx = x; x 2 X , называется тождественным отображением.
Отображения множеств можно задавать с помощью таблиц, графиков, стрелочных схем.
Строя таблицу отображения f : A ! B, в ней записывают всевозможные
пары (a; '(a)); a 2 A: |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
или |
'(a1) |
'(a2) |
. . . |
'(an). |
: |
|
'(x) |
'(a1) |
'(a2) |
. . . |
'(an) |
||||||
|
x |
a1 |
a2 |
. . . |
an |
|
a1 |
a2 |
. . . |
an |
|
|
|
|
|
|
|
|
|
|
|
|
|
Разумеется, эта таблица полностью задает отображение ' только в случае конечного множества A = fa1; :::; ang , то есть множества, состоящего из определенного числа элементов.
С помощью стрелочных схем, которые также называются графами, отображение ' : A ! B задается так: элементы множеств A и B обозначают различными точками плоскости (для множества A – слева, а для B – справа). Затем каждую из точек, которыми обозначены элементы множества A, соединяют стрелкой слева направо с точкой, которой обозначен соответствующий элемент множества B. Задание отображения с помощью графа наиболее удобно для конечных множеств.
Пример 6. Пусть A = f3; 2; 6; 7g; B = f28; 12; 4; 5; 11; 14g; ' : A ! B –
отображение, которое каждому числу из A ставит в соответствие наименьшее
