
Лекции по алгебре.Баскаков
.pdf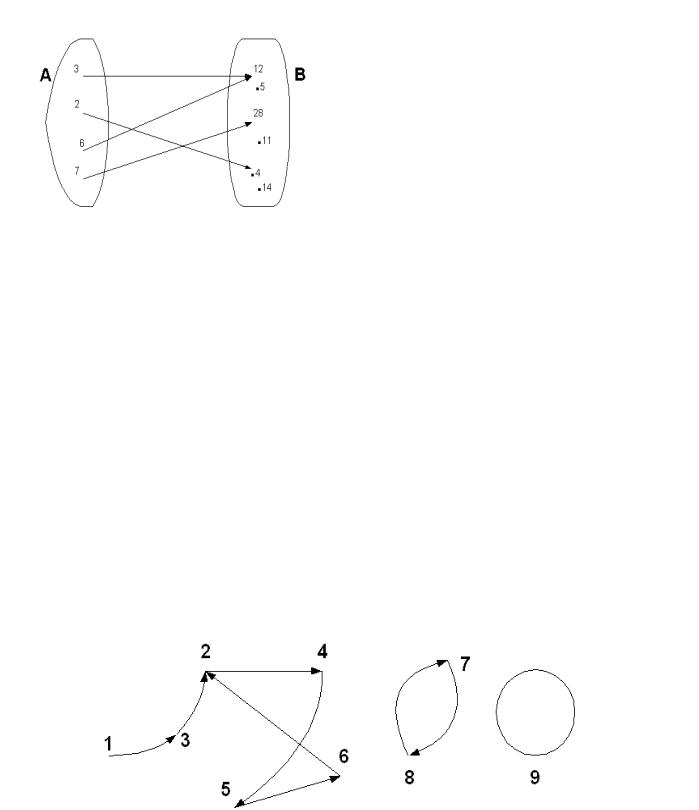
x 3: Отображения множеств и классификация отображений |
17 |
общее кратное этого числа и числа 4. Это отображение полностью описывается следующей стрелочной схемой
Рис. 4
Стрелочные схемы (графы преобразований) для отображений множества в себя можно строить несколько по-иному.
Пример 7. Пусть A = fa1; : : : ang – конечное множество и ' : A ! A
– отображение. Обозначим каждый элемент множества A точкой на плоскости так, чтобы разным элементам отвечали различные точки, при этом для этих точек плоскости сохраним обозначения соответствующих элементов из A: Две точки соединим стрелкой от a к b тогда и только тогда, когда выполнено условие '(a) = b. Так получим граф отображения ' : A ! A. Ясно, что он однозначно определяет преобразование '.
В частности, если A = f1; 2; 3; 4; 5; 6; 7; 8; 9g и отображение ' : A ! A задано таблицей
' = |
1 2 3 4 5 6 7 8 9 |
; |
|
|
3 4 2 5 6 2 8 7 9 |
то получим следующий граф
Рис. 5
18 |
Глава 1. Элементы теории множеств |
Сразу отметим, что разнообразные отображения постоянно будут возникать при чтении этого курса и мы постараемся отмечать появление наиболее важных из них.
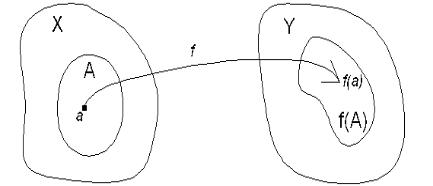
Определение 2. Пусть f : X ! Y – отображение и A – подмножество из X . Множество
f(A) = fy 2 Y : y = f(x); x 2 Ag
называется образом множества A при отображении f (см. рис.6)
Рис. 6
Ясно, что f(;) = ;: Для функции f : R ! R; f(x) = x2 образом множеств A1 = [ 1; 1] и A2 = [0; 1] служит одно и то же множество [0,1] (таким образом, f(A1) = f(A2) = A2):
Определение 3. Пусть f : X ! Y – отображение и B – подмножество из Y . Множество
f 1(B) = fx 2 X : f(x) 2 Bg
называется прообразом множества B при отображении f .
Для функции f : R ! R; f(x) = x2 прообразом отрезка B = [0; 1] служит отрезок [ 1; 1].
В следующих трех определениях проводится некоторая (грубая) классификация отображений.
Определение 4. Отображение f : X ! Y называется взаимно однозначным или инъективным, если из условия f(x1) = f(x2) следует, что x1 = x2 , то есть разные элементы из X переводятся отображением f в разные элементы из Y .
Например, отображение f0 : R ! R; f0(x) = x3 инъективно, но отображение g : R ! R; g(x) = x2 не инъективно, так как
g(a) = g( a) 8 a 2 R:

x 3: Отображения множеств и классификация отображений |
19 |
Определение 5. Отображение f : X ! Y называется сюръективным (или отображением на), если f(X) = Y , то есть для любого элемента y 2 Y существует хотя бы один элемент x из X такой, что f(x) = y:
Рассмотренное (перед определением 5) отображение f0 сюръективно, а отображение g таким не является (так как g(R) = [0; 1)):
Определение 6. Отображение f : X ! Y называется взаимно однозначным отображением на или биективным, если оно инъективно и сюръективно одновременно.
Таким образом, отображение f биективно, а отображение g нет. Биективным отображением является тождественное отображение IX : X ! X (X – произвольное множество).
Определение 7. Пусть f : X ! Y – биективное отображение. Тогда для любого элемента y 2 Y существует хотя бы один элемент x 2 X такой, что f(x) = y (используется сюръективность отображения f ) и такой элемент x единствен (это следует из инъективности f ). Итак, каждому элементу y из Y поставлен в соответствие единственный элемент x 2 X . Полученное отображение f 1 : Y ! X называется обратным к отображению f (см. рис.7).
Рис. 7
Обратным к отображению f0 : R ! R; f0(x) = x3 является отображение f0 1(x) = p3 x. Ясно, что IX1 = IX для любого множества X . Функции f; g : R ! R; f(x) = x2; g(x) = sin x не биективны. Однако, если изменить их область определения и область значений, то они (все-таки, это будут другие функции!) станут биективными.
Определение 8. Пусть ' : X ! Y – отображение и X0; Y0 – подмножества из X и Y соответственно, для которых '(X0) Y0 (т.е. '(x0) 2 Y0 8x0 2 X0 ). Отображение '0 : X0 ! Y0 , определенное равенствами '0(x0) = = '(x0) 8x0 2 X0 , называется сужением (ограничением) отображения ' на
X0 .
20 |
|
|
Глава 1. |
|
Элементы теории множеств |
||
Вернемся к рассмотрению функций f(x) = x2 и g(x) = sin x. Если поло- |
|||||||
жить X0 = R+ |
0 = Y0 для функции f и X0 = [ =2; =2]; Y0 = [ 1; 1] для |
||||||
функции |
g |
, то |
сужения f |
|
и g |
|
отображений f и g на соответствующее под- |
|
S |
0 |
|
0 |
|
||
множество X0 будут биективными отображениями. Обратные к ним имеют
вид p
f0 1(x) = x; f0 1 : R+ [ 0 ! R+ [ 0; g0 1(x) = arcsin(x); g0 1 : [ 1; 1] ! [ =2; =2]:
К понятию обратного отображения можно подойти несколько с другой стороны, используя определение суперпозиции отображений.
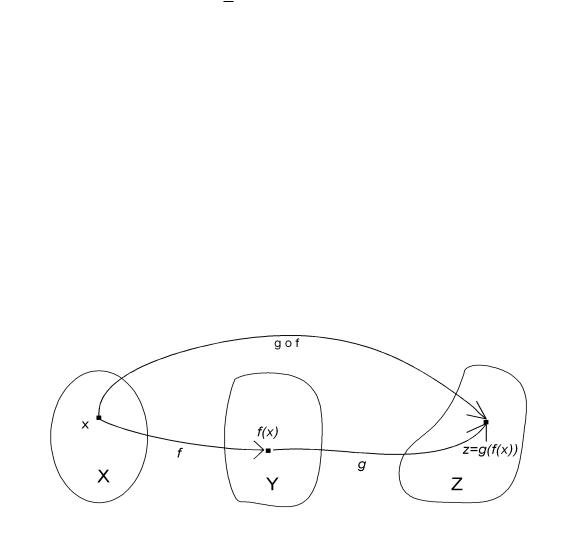
Определение 9. Пусть X; Y; Z – три множества и f : X ! Y и g : Y ! Z – два отображения. Суперпозицией отображений f и g (или сложной функцией) называется отображение (см.рис.8), обозначаемое символом g f(g f : X ! Z) и определяемое формулой
(g f)(x) = g(f(x)); x 2 X:
Обратим особое внимание на запись суперпозиции, которая читается справа налево, а не слева направо, ибо (g f)(x) есть g(f(x)).
Рис. 8
Рассмотрим две функции f; g : R ! R; f(x) = x2; g(x) = sin x: Тогда их суперпозицией является функция h = g f : R ! R; h(x) = sin x2: Важно заметить, что (f g)(x) = sin2x и поэтому f g 6= g f:
Отметим еще, что если ' : X ! Y – произвольное отображение, то
' IX = IY ' = ':
Определение 10. Отображение f : X ! Y называется обратимым, если существует такое отображение g : Y ! X , что имеют место равенства
g f = IX; f g = IY |
(1) |

x 3: Отображения множеств и классификация отображений |
21 |
Т е о р е м а 1. Отображение f : X ! Y обратимо тогда и только тогда, когда оно биективно.
Доказательство. Необходимость. Пусть f обратимо. Тогда существует отображение g : Y ! X , для которого имеют место равенства (1). Если x1; x2 – два элемента из множества X и f(x1) = f(x2); то из первого равенства (1) получаем
x1 = (g f)(x1) = g(f(x1)) = g(f(x2)) = x2;
т.е. отображение f инъективно.
Для проверки его сюръективности используется второе равенство из (1). Если y – произвольный элемент из Y , то имеет место равенство y = (f g)(y) = f(x), где x = g(y), т.е. f – сюръективное отображение.
Достаточность. Если f – биективное отображение, то непосредственно
из определения 7 следует, что имеют место равенства |
|
f 1 f = IX; f f 1 = IY ; |
(2) |
т.е. f – обратимое отображение. Теорема доказана.
Согласно теореме 1, обратимое отображение f : X ! Y всегда биективно и поэтому обратное отображение единственно.
Т е о р е м а 2 (об ассоциативности суперпозиции отображений).
Пусть f : X1 ! X2; g : X2 ! X3; h : X3 ! X4 – три отображения. Тогда имеет место равенство
(h g) f = h (g f):
Доказательство немедленно следует из равенств
((h g) f)(x) = (h g)(f(x)) = h(g(f(x))) =
= h((g f)(x)) = (h (g f))(x); x 2 X:
Теорема 2 позволяет корректно ввести понятие суперпозиции нескольких отображений f; g; h. Можно, например, положить h g f = h (g f) и при этом не заботиться о расстановке скобок.
Определение 11. Пусть f : X ! X – отображение и n – натуральное число. Положим fn = f f f . Отображение fn X ! X назовем
n раз |
|
|
|
|
|
|
||
f(n |
показатель степени). |
|
|
|
|
|||
степенью отображения| |
–{z2 |
} |
2 |
4 |
; g |
3 |
6 |
; : : : : |
Например, если g(x) = x ; |
g : R ! R; то g |
|
(x) = x |
|
(x) = x |
|||
Ясно, что IXn = IX 8n 2 N:
22 |
Глава 1. Элементы теории множеств |
Для обратимого отображения f : X ! X можно еще ввести отображение f n : X ! X; положив f n = (f 1)n: Ясно (это вытекает из теоремы 2), что f n – отображение обратное к fn .
Т е о р е м а 3. Пусть f : X ! Y; g : Y ! Z – два обратимых (биективных) отображения. Тогда их суперпозиция g f является также обратимым (биективным) отображением и (g f) 1 = f 1 g 1 (т.е. обратное отображение к суперпозиции отображений есть суперпозиция обратных к g и f отображений, но взятых в другом порядке сомножителей).
Доказательство. Из теоремы 2 следуют равенства
(g f) (f 1 g 1) = g (f f 1) g 1 = g IY g 1 = g g 1 = IZ:
Аналогично проверяется равенство (f 1 g 1) (g f) = IX . Таким образом, отображение g f обратимо (следовательно, биективно) и (g f) 1 = f 1 g 1: Теорема доказана.
Следующие два понятия используются нами далее, они тесно связаны с понятием отображения.
Определение 12. Пусть X – непустое множество. Отображение x : N ! X называется последовательностью. Для задания последовательности x : N ! X достаточно выписать упорядоченный (элементами из N ) набор элементов (x1; x2; : : : ); и тогда x(k) = xk . В связи с этим последовательности обозначают символом (x1; x2; : : : ) или, короче, (xk):
Определение 13. Отображение f : X1 X2 Xn ! Y; n 2, определенное на произведении нескольких множеств, называется отображением (функцией) нескольких переменных.
Упражнения к § 3
1. Постройте графы преобразований, заданных таблицами:
a) |
5 6 1 8 3 7 2 4 ; b) |
6 8 5 4 3 7 1 3 |
; |
|
|
1 2 3 4 5 6 7 8 |
; d) |
1 2 3 4 5 6 7 8 |
|
c) |
6 4 3 7 5 1 2 |
6 4 1 8 4 3 4 9 9 |
: |
|
|
1 2 3 4 5 6 7 |
|
1 2 3 4 5 6 7 8 9 |
|
2.Какие из преобразований a)-d) из задачи 1 инъективны, сюръективны, биективны?
3.Пусть f : X ! Y – отображение и B; C – подмножества из Y .
Докажите, что имеют место равенства
а) f 1(B SC) = f 1(B) Sf 1(C);

x 3: Отображения множеств и классификация отображений |
23 |
||||||
|
|
|
б) f 1(Y n B) = X n f 1(B); |
|
|||
|
f : X |
|
в) f 1(B C) = f 1(B) f 1(C): |
|
|||
4. Пусть |
! |
Y |
– |
отображение и A; B – подмножества из X . |
|
||
|
|
T |
T |
|
|||
Докажите, что имеют место следующие соотношения
A B =) f(A) f(B);
TT
f(A B) f(A) f(B);
SS
f(A B) = f(A) f(B):
5. Докажите, что для любого отображения f : X ! X имеют место включения
f(X) f2(X) f3(X) : : : :
6.Приведите пример отображения f : X ! Y и подмножества B Y такого, что f 1(B) = ; (рассмотрите f(x) = x2; f : R ! R):
7.Приведите пример отображения f : X ! X и двух подмножеств A; B
TT
из X таких, что f(A B) 6= f(A) f(B):
8.Приведите пример отображения f : N ! N , которое а) инъективно, но не сюръективно; б) сюръективно, но не инъективно.
9.Пусть X – конечное множество. Докажите, что если f : X ! X – инъективное отображение, то оно сюръективно (и, следовательно, биективно).
10. Найдите суперпозиции g f и f g функций f; g : R ! R, если а) f(x) = 2x + 3; g(x) = 3x + 4;
б) f(x) = x3 + 5x2; g(x) = x2 + 3; в) f(x) = x2 + 2; g(x) = x3 + x2 + 1.
11. Пусть f : R n f 1g ! R n f 1g – функция, определенная формулой
f(x) = x 3: Найдите f2 и f3 . x + 1
12. Какие из следующих отображений множества R и R обратимы: а) f1(x) = xn (n – натуральное число);
б) f2(x) = 2x;
в) f3(x) = ax + b; a; b 2 R; a 6= 0; г) f4(x) = cos x?
Найдите обратные к обратимым отображениям.
13.Пусть f : X ! Y – обратимое отображение. Докажите, что тогда отображение f 1 : Y ! X обратимо и (f 1) 1 = f .
14.Пусть f : X ! X – обратимое отображение. Докажите, что для любого натурального n отображение fn обратимо и (fn) 1 = f n .
15.Докажите единственность обратного для обратимого отображения.

24 |
Глава 1. Элементы теории множеств |
16.Пусть f : X ! Y – отображение. Докажите, что если существует отображение g : Y ! X такое, что g f = IX , то f –инъективное отображение. Отображение g называют левым обратным для f .
17.Докажите, что если для отображения f : X ! Y существует отображение g : Y ! X такое, что f g = IY , то f – сюръективное отображение. Отображение g называют правым обратным для f .
18.Пусть X и Y - конечные множества с числом элементов n и m соответственно. Найти число
а) отображений; б) инъективных отображений;
в) сюръективных отображений множества X в множество Y .
x 4. Сравнение множеств. Мощность множества
Множества бывают конечные и бесконечные. Конечным называется множество, состоящее из нескольких элементов. Любые два конечных множества можно сравнивать по числу элементов и говорить об одинаковом количестве элементов или о том, что в одном множестве число элементов меньше, чем число элементов второго. Однако в вопросах сравнения двух множеств можно поступить несколько по-иному, заметив, что два конечных множества X и Y имеют одинаковое количество элементов тогда и только тогда, когда существует биективное отображение f : X ! Y (т.е. между множествами X и Y можно установить взаимно однозначное соответствие). Этот подход позволяет ввести следующее понятие.
Определение 1. Два множества X и Y называются эквивалентными (будет использоваться обозначение X Y ), если существует биективное отображение f : X ! Y:
Определение 2. Множество X называется бесконечным, если оно не эквивалентно никакому конечному множеству.
Т е о р е м а 1. Введенное в классе всех множеств бинарное отношение является отношением эквивалентности.
Доказательство. Если X Y , то существует биективное отображение f : X ! Y . В силу теоремы 1 из x 1 оно обратимо и поскольку обратное отображение f 1 : Y ! X также биективно (см. задачу 13 из x 3), то Y X .
Ясно, что X X (тождественное отображение IX биективно). Наконец, если X Y; Y Z и f : X ! Y; g : Y ! Z – биективные отображения, то в силу теоремы 3 из x 3 их суперпозиция g f : X ! Z есть снова биективное отображение и поэтому X Z: Теорема доказана.
x 4: Сравнение множеств. Мощность множества |
25 |
Таким образом, класс всех множеств (мы избегаем термина множество всех множеств) разбивается на непересекающиеся классы эквивалентности.
Определение 3. Два множества, входящие в один класс эквивалентности, называются равномощными или про такие множества говорят, что они имеют одинаковую мощность или одинаковое кардинальное число.
Пусть n – натуральное число. Тогда класс эквивалентности, содержащий множество f1; 2; : : : ; ng, состоит из всех конечных множеств, содержащих ровно n элементов. Таким образом, понятие мощности множества (кардинального числа) является непосредственным обобщением понятия числа.
Определение 4. Множество X называется счетным, если оно эквивалентно множеству N натуральных чисел.
Следующие примеры показывают, что при рассмотрении бесконечных множеств следует проявлять большую осторожность.
Пример 1. Множество N2 четных натуральных чисел счетно. Для доказательства следует рассмотреть биективное отображение f(n) = 2n;
f : N ! N2: Таким образом, подмножество N2 из N эквивалентно самому множеству N: Разумеется, таким свойством могут обладать только бесконечные множества.
Пример 2. Любые два отрезка [a,b] и [c,d] имеют одинаковую мощность,
так как отображение |
f : [a; b] |
! |
[c; d]; f(x) = |
d cx + |
bc da |
биективно. |
||
|
|
b a |
|
b a |
|
|||
Определение 5. Множества, эквивалентные отрезку [0,1], называются
множествами мощности континуума.
Из примера 2 следует, что любой отрезок из [0,1] имеет мощность континуума.
Т е о р е м а 2. Множество Q рациональных чисел счетно. Доказательство. Каждое рациональное число однозначно записы-
вается в виде несократимой дроби = p=q; q > 0. Число jpj + q назовем высотой рационального числа : Отметим, что имеется лишь конечное число рациональных чисел, имеющих данную высоту n 2 N: Пронумеруем все рациональные числа по возрастанию высоты, т.е. вначале выпишем числа высоты 1 (имеется только одно число 0/1=0 такой высоты), затем высоты 2 (это числа 1=1 и 1=1); высоты 3 и т.д. При этом всякое рациональное число получит некоторый номер, т.е. построено биективное отображение ' : Q ! N: Теорема доказана.
Бесконечное множество, не являющееся счетным множеством, называется несчетным множеством.
Г.Кантором было доказано (см., например, [7]), что отрезок [0,1] – несчетное множество.
26 |
Глава 1. Элементы теории множеств |
Упражнения к § 4
1. Докажите счетность следующих двух множеств f2; 3; 4; : : : g f1; 3; 5; : : : ; 2n + 1; : : : g:
2.Докажите счетность множества Z целых чисел.
3.Докажите эквивалентность интервала (0,1) и множества R:
4.Докажите эквивалентность интервала (a; b) и отрезка [a; b].
