
Лекции по алгебре.Баскаков
.pdfx 16: Линейные нормированные пространства |
97 |
12.Покажите, что линейное пространство C[ 1; 1] есть прямая сумма подпространств нечетных и четных функций (рекомендация: учтите, что f(x) = [f(x) f( x)]=2 + [f(x) + f( x)]=2):
13.Найдите размерность произведения X1 X2 для линейных пространств X1 и X2 .
14.Пусть X1 и X2 – подпространства из линейного пространства X со свой-
T
ством dim X1 + dim X2 > dim X: Докажите, что dim(X1 X2) 1:
15.Для любых подпространств X1 X2 из линейного пространства X через X1+X2 обозначим множество векторов вида fx1+x2 : x1 2 X1; x2 2 X2g:
Докажите, что X1 + X2 |
- линейное подпространство и dim(X1 + X2) = |
||||||||||||||
= dimX1 + dimX2 dimX1 |
TX2: |
X ; |
|
|
i |
3 линей- |
|||||||||
16. Докажите, что для любых трех подпространств |
i |
1 |
|
||||||||||||
(X1 |
X2) |
X3 = X1 |
(X2 |
X3): |
|
|
|
1 L |
X |
2 L |
X |
3 |
= |
||
ного пространства X имеют место равенства X = X |
|
|
|
|
|||||||||||
L |
L |
L |
|
L |
|
|
|
|
|
|
|
|
|
|
|
x 16. Линейные нормированные пространства
Множество, наделенное некоторой структурой, т.е. множество с установленными соотношениями между его элементами или операциями над ними, называют пространством. Обычно структуру множества относят к числу геометрических либо алгебраических структур. Так, линейные пространства есть множества, наделенные определенными алгебраическими структурами. В этом параграфе мы введем понятие расстояния, которое по своей природе является геометрическим. Определяемые далее линейные нормированные пространства одновременно наделяются двумя структурами: алгебраической (являясь линейным пространством) и геометрической (на нем введено понятие расстояния), причем эти структуры определенным образом согласованы.
Определение 1. Пусть X – непустое множество. Расстоянием или метрикой на X называется функция : X X ! R, удовлетворяющая следующим свойствам (аксиомам):
1) |
(x; y) 0; (x; y) = 0 () x = y (аксиома тождества); |
2) |
(x; y) = (y; x) (свойство симметрии); |
3) |
(x; y) (x; z) + (y; z) (неравенство треугольника); |
которые выполняются для всех элементов x; y; z 2 X: Число (x; y) называется расстоянием между элементами x и y. Множество X , на котором опре-

98 Глава 3. Линейная алгебра
делено расстояние ; называется метрическим пространством; для него используется обозначение (X; ):
Пример 1. Пусть X = R или X = C: Тогда функция (x; y) = jx yj; : X X ! R является расстоянием.
Пример 2. Пусть X = Rn ( X = Cn): Множество Rn (или Cn) становится метрическим пространством, если ввести расстояние формулой
n |
!1=2 |
Xi |
jxi yij2 : |
(x; y) = |
|
=1 |
|
Пример 3. Пусть X – произвольное непустое множество. Положим d(x; y) = 1; если x 6= y и d(x; y) = 0 для x = y: Функция d : X X ! R
является расстоянием. Такое метрическое пространство называется дискретным.
Определение 2. Пусть X – метрическое пространство с метрикой; x0 2 X и r > 0: Множества
B(x0; r) = fx 2 X : (x; x0) < rg;
B(x0; r) = fx 2 X : (x; x0) rg;
S(x0; r) = fx 2 X : (x; x0) = rg = B(x0; r) n B(x0; r)
называются соответственно открытым шаром, замкнутым шаром и сферой
с центром в точке x0 2 X и радиусом r > 0:
Отметим, что в дискретном метрическом пространстве сфера S(x0; r) пуста, если r < 1:
Определение 3. Последовательность (xn) = (x1; x2; : : : ) элементов метрического пространства X называется сходящейся к элементу x0 2 X; если
lim (xn; x0) = 0 или 8 " > 0 9N 2 N; что (xn; x0) < " 8n 2 N: Эле-
n!1
мент x0 называется пределом последовательности (xn) и используется запись
lim xn = x0:
n!1
Определение 4. Последовательность (xn) из метрического пространства X называется фундаментальной или последовательностью Коши, если
8" > 0 9N 2 N такое, что (xn; xm) < " 8n; m > N:
Т е о р е м а 1. Всякая сходящаяся к элементу x0 из метрического пространства (X; ) последовательность (xn) является фундаментальной.
Доказательство. Пусть " > 0: Из условия сходимости последовательности (xn) к элементу x0 следует существование числа n0 2 N такого, что

x 16: Линейные нормированные пространства |
99 |
(xn; x0) < "=2 8n > n0: Тогда для любых n; m > n0 из неравенства треугольника получаем
(xn; xm) (xn; x0) + (xm; x0) < ":
Теорема доказана.
Определение 5. Метрическое пространство X называется полным, если всякая фундаментальная последовательность из X сходится к некоторому элементу из X .
Отметим, что метрические пространства R и C полны. Примеры других полных метрических пространств будут указаны несколько позже.
В линейных пространствах расстояние обычно определяют, используя понятие нормы (длины) векторов.
Определение 6. Линейное пространство X над полем K , которое совпадает с R либо с C, называется нормированным, если задана функция ' : X ! R (величина '(x) называется нормой вектора x и обозначается символом jjxjj), удовлетворяющая следующим условиям (аксиомам):
1)jjxjj 0 и jjxjj = 0 () x = 0;
2)jj xjj = j jjjxjj;
3)jjx + yjj jjxjj + jjyjj;
для любых векторов x; y 2 X и любого числа 2 K .
Замечание 1. Любое линейное нормированное пространство X является метрическим, если положить (x; y) = jjx yjj; x; y 2 X: Если выполнение первых двух свойств расстояния очевидно, то неравенство треугольника следует из свойства 3) нормы:
(x; y) = jjx yjj = jjx z + z yjj jjx zjj + jjz yjj = (x; z) + (y; z):
Таким образом, все понятия для метрических пространств естественным образом формулируются для линейных нормированных пространств. Так, например, последовательность (xn) из линейного нормированного пространства
X называется сходящейся к вектору x0 2 X; если lim jjxn x0jj = 0.
n!1
Особо выделим шар B(0; 1) = fx 2 X : jjxjj 1g; который обозначим символом B1 или B(1):
Рассмотрим несколько примеров линейных нормированных пространств.
Пример 4. Линейное пространство Kn , где K = R, либо K = C; является нормированным. Например, можно ввести на следующие три нормы
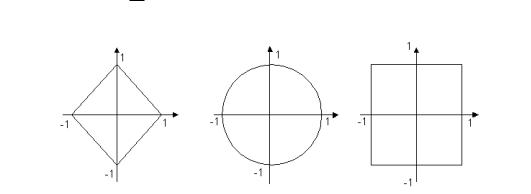
100 |
|
|
|
|
|
|
|
|
Глава 3. Линейная алгебра |
|
|
|
|
|
n |
|
|
|
|
1=2 |
|
jjxjj1 |
|
iP |
|
|
|
|
|
|||
= |
jxij |
|
|
(октаэдрическая норма), |
||||||
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
jjxjj2 |
= i=1 |
jxij2 |
(евклидова |
норма), |
||||||
jj |
x |
jj3 |
= |
max |
j |
x |
ij |
|
(кубическая |
норма), |
|
1=i n |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
где x = (x1; : : : ; xn) 2 Kn:
В зависимости от выбора одной из трех указанных норм в R2 получаем следующие три шара B(0; 1) соответственно
Рис. 14
Пример 5. Линейное пространство C[a; b] является нормированным, если ввести норму следующей формулой
jjxjj = max jx(t)j; x 2 C[a; b]:
t2[a;b]
Конечность величины jjxjj для x 2 C[a; b] следует из теоремы Вейерштрасса. Первые две аксиомы нормы проверяются совсем легко (проверьте !). Докажем выполнение третьей аксиомы. Если x; y; z – функции из C[a; b], то для любого t0 2 [a; b] имеет место неравенство
jx(t0) + y(t0)j jx(t0)j + jy(t0)j max jx(t)j + max jy(t)j jjxjj + jjyjj
t2[a;b] t2[a;b]
x |
+ |
y |
max |
j |
x(t ) + y(t ) |
j jj |
x |
jj |
+ |
y |
jj |
: |
||
и, следовательно, jj |
|
jj = t0 |
[a;b] |
0 |
0 |
|
jj |
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Пример 6. В каждом из линейных пространств Pn(K) (где K = R или K = C), C[a; b] введем в рассмотрение следующие две нормы
f |
max f(t) ; |
|
jj jj1 |
= t |
[a;b] j j |
|
2 |
|
jjfjj2 = Za |
b |
|
jf(t)jdt; |
||

x 16: Линейные нормированные пространства |
101 |
где a; b 2 R и a < b: Отметим, что если jjfjj1 = 0; то f(t) = 0 8t 2 [a; b] и поэтому в силу основной теоремы высшей алгебры f = 0. Если же jjfjj2 =
b |
|
|
то из непрерывности функции '(t) = jf(t)j следует, что |
||||||||
a |
jf(t)jdt |
= 0; |
|||||||||
b |
t |
8 |
2 b |
a; b |
; |
и поэтому снова |
f |
= 0. Далее ясно, что |
jj |
jj |
|
f |
t |
|
f |
|
|
||||||
R |
( ) = 0 |
|
[ |
] |
|
|
|
2 |
= |
||
RR
j f(t)jdt = j j jf(t)jdt = j j jjfjj2; т.е. выполнена вторая аксиома нормы.
a |
a |
|
|
|
b |
|
b |
Если f; g 2 |
Pn(K); то jjf + gjj2 = Ra |
jf(t) + g(t)jdt |
Ra (jf(t)j + jg(t)j)dt = |
bb
RR
jf(t)jdt + jg(t)jdt = jjfjj2 + jjgjj2: Выполнение второй и третьей аксиом
aa
для первой нормы фактически проверено в предыдущем примере. Определение 7. Пусть X – линейное нормированное пространство и
jj jj1; jj jj2 – две нормы на X . Они называются эквивалентными, если существуют две постоянные C1; C2 > 0 такие, что
|
|
|
|
|
|
C1jjxjj2 jjxjj1 C2jjxjj2 8x 2 X |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
(и, следовательно, C2 1jjxjj1 jjxjj2 C1 1jjxjj1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Важным свойством эквивалентных норм является тот факт, что сходи- |
|||||||||||||||||||||||||||||||||
мость последовательности (xn) |
|
из X по одной норме влечет ее сходимость |
||||||||||||||||||||||||||||||||
по второй норме. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Т е о р е м а 2. Введенные в примере 4 нормы эквивалентны. |
|
||||||||||||||||||||||||||||||||
|
3 |
|
1 |
|
т.е. нормы |
|
|
1 |
и |
3 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
= |
P |
x |
|
|
|
|
n max |
x |
|
|
= n x |
и |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
i=1 j |
ij |
|
kj |
||||||||||||||||
jj |
Доказательство. Поскольку jj jj1 |
|
|
|
|
|
1 k n j |
|
|
jj jj3 |
||||||||||||||||||||||||
jj jj jj |
|
; |
|
|
jj jj |
|
1=2jj jj |
эквивалентны. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
x |
|
x |
|
|
i=1 jxij2 |
|
|
jjxjj2; т.е. jjxjj2 |
и |
|||||||||||||||||||||||||
|
Далее, |
jjxjj2 = |
|
pnjjxjj3 и |
jjxjj3 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jj |
jj |
|
|
|
|
Следовательно, эквивалентны |
jj jj |
|
и |
jj jj |
|
|
(докажите!). |
|||||||||||||||||||||
x |
3 эквивалентны. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|||||||
Теорема доказана. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Замечание 2. Можно доказать, что любые две нормы в конечномерном |
|||||||||||||||||||||||||||||||||
линейном пространстве эквивалентны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Пример 7. Нормы из примеров 5 и 6, рассматриваемые в C[a; b]; не эк- |
|||||||||||||||||||||||||||||||||
вивалентны. |
|
Для |
этого |
достаточно |
|
рассмотреть |
|
последовательность |
||||||||||||||||||||||||||
'n(t) = tn |
(для определенности мы рассматриваем случай a = 0; b = 1; |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
jj |
|
|
jj |
|
|
|
|
n+1 |
|
|
|
n |
|
|
jj |
|
jj |
|
|||
т.е. пространство C[0; 1]): Поскольку |
|
'n |
|
2 = |
p |
1 |
|
|
; то lim |
|
|
|
'n 2 = 0: С |
|||||||||||||||||||||
другой стороны, jj'njj1 = |
0maxt 1 jtnj = 1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!1 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание. Сходимость по норме пространства C[a; b] |
|
(см.пример 5) |
|||||||||||||||||||||||||||||||
называют равномерной сходимостью.

102 |
Глава 3. Линейная алгебра |
Упражнения к § 16
1.Докажите, что последовательность xk = (xk1; xk2; ; xkn); k 1 из Kn (где K = R или K = C) сходится к вектору
x0 = (x0k) = (x01; x02; ; x0n) по одной из норм в Kn (см. пример 4) тогда и только тогда, когда каждая числовая последовательность (xkj) K; (1 j n) сходится к x0j:
2. Будет ли фундаментальной в C[0; 1] (см. пример 5) последовательность функций: a) 'n(t) = tn; n 1; б) fn(t) = sin n1 t; n 1?
3.Сходятся ли в пространство C[0; 1] следующие последовательности: а) xn(t) = tn tn+1; б) yn(t) = tn + t2n; в) tnn+1+1 tnn+2+2 ; n 1?
4.Найдите предел последовательности функций 'n(t) = cos n1 t в C[0; 1]:
5.Докажите неравенство jjjxjj jjyjjj jjx yjj для любой пары векторов из линейного нормированного пространства X:
6.Пусть в конечномерном линейном пространстве X введены две нормы jj jj1; jj jj2: Докажите существование таких констант r1; r2 > 0; что имеют место включения
B2(0; r1) B1(0; 1) B2(0; r2);
где B1(0; 1) – шар относительно первой нормы и B2(0; r) – шар относительно второй нормы.
7. Для f 2 Pn(C) положим jjfjj = max jf(zk)j: Для каких комплексных
1 k m
чисел z1; : : : ; zm эта формула определяет норму на Pn(C)?
8. Докажите, что последовательность xn из (X; ) фундаментальная тогда
и только тогда, когда lim (xn; xm) = 0:
k;m!1
x 17. Пространства со скалярным произведением. Евклидовы пространства
В предыдущем параграфе мы рассматривали линейные нормированные пространства, т.е. линейные пространства, в которых введено понятие длины вектора (и, значит, расстояния между векторами). Однако до сих пор не было введено понятий угла между двумя векторами, перпендикулярных векторов

x 17: Пространства со скалярным произведением. Евклидовы пространства |
103 |
и других важных геометрических понятий. Все это оказывается возможным в линейных пространствах со скалярным произведением. Именно рассмотрению таких пространств посвящен данный параграф.
Определение 1. Пусть поле K есть либо R, либо C: Линейное пространство H над полем K называется пространством со скалярным произведением, если задана функция ' : H H ! K (значение '(x; y) функции ' на каждой паре векторов x; y из H обозначается символом (x; y)), которая удовлетворяет следующим свойствам (аксиомам):
1)(x; x) 0; (x; x) = 0 () x = 0;
2)(x + y; z) = (x; z) + (y; z);
3)( x; y) = (x; y);
4)(x; y) = (y; x);
для любых 2 K и x; y; z 2 H: Число (x; y) называется скалярным произведением векторов x и y.
Ясно, что при K = R условие 4) выглядит так: (x; y) = (y; x): Из свойств 3) и 4) получим, что имеет место свойство 30)(x; y) = (x; y) (см.задачу 1), а из свойств 2) и 4) следует, что верно свойство 20)(x; y + z) = (x; y) + (x; z):
Определение 2. Конечномерное линейное пространство со скалярным произведением называется евклидовым пространством.
Рассмотрим примеры пространств со скалярным произведением и, в частности, евклидовых пространств.
Пример 1. Линейное пространство V 3 свободных векторов физического пространства является трехмерным евклидовым пространством. Скалярное произведение векторов a; b 2 V 3 задается равенством
(a; b) = jajjbjcos ';
где jaj; jbj – длины векторов a; b и ' – угол между векторами a и b. Свойства скалярного произведения доказываются в аналитической геометрии.
Пример 2. Рассмотрим линейное пространство Kn , где K = R; либо K = C. Для любой пары векторов x = (x1; ; xn); y = (y1; ; yn) 2 Kn их скалярное произведение определяется формулой
n |
|
|
n |
X |
|
|
X |
(x; y) = |
xi |
y |
i ( = xiyi; K = R): |
i=1 |
|
|
i=1 |
Легко проверяется, что Kn является евклидовым пространством.
Пример 3. Рассмотрим комплексное (вещественное) линейное простран-

104 Глава 3. Линейная алгебра
ство C[a; b] и для любых двух функций x; y 2 C[a; b] |
положим |
||||
b |
|
|
|
b |
|
(x; y) = Za |
x(t) |
|
(t)dt ( = Za |
x(t)y(t)dt; |
K = R): |
y |
|||||
Отметим, что если z 2 C[a; b] – комплекснозначная функция, то по определению
b |
|
b |
b |
Za |
z(t)dt = Za |
Rez(t)dt + i Za |
Imz(t)dt: |
Из известных свойств интеграла получаем выполнение всех свойств скалярного произведения (проверьте !). Итак, C[a; b] – бесконечномерное пространство со скалярным произведением.
Пример 4. Формула
w
Z
(x; y) = x(t)y(t)dt
0
задает скалярное произведение в Cw:
Пример 5. В пространстве Pn(C) определим скалярное произведение с
помощью формулы
n
X
(f; g) = fkgk;
k=0
если f(z) = f0 + f1z + + fnzn; g(z) = g0 + g1z + + gnzn: В том же линейном пространстве используется также скалярное произведение вида
(f; g)1 = Za |
b |
f(t)g(t)dt; |
где a; b – фиксированные числа из R; причем a < b:
Замечание 1. Каждое пространство H со скалярным произведением можно сделать нормированным, если положить
p
jjxjj = (x; x); x 2 H:
Первые две аксиомы нормы непосредственно следуют из свойств 1) и 3) скалярного произведения, а выполнение третьей аксиомы нормы проверим несколько позже.
В применении к пространствам из примеров 1) - 5) получим в соответствующих пространствах следующие нормы
x 17: Пространства со скалярным произведением. Евклидовы пространства |
105 |
||||||||||
|
|
n |
|
|
1=2 |
|
|
|
|
||
|
|
P |
|
|
|
1=2 |
|
|
|||
jjxjj = i=1 jxij2 |
|
! |
(евклидова норма в Cn); |
|
|||||||
jjxjj = |
|
ab jx(t)j2dt |
(норма |
в C[a; b] и Pn); |
|
||||||
|
|
R |
|
|
|
|
|
1=2 |
|
|
|
jjxjj = |
w |
jx(t)j2dt |
|
(норма |
в Cw) |
|
|||||
0 |
|
|
|||||||||
jjfjj = |
|
Rn |
|
|
1=2 |
|
(норма в Pn): |
|
|||
k=0 jfkj2 |
|
|
|
|
|
||||||
|
|
P |
|
|
|
|
|
|
|
|
|
Далее символом H обозначается линейное пространство со скалярным произведением.
Определение 3. Два вектора x; y из H называются ортогональными (перпендикулярными), если их скалярное произведение (x; y) равно нулю (в этом случае будет использовано обозначение x?y).
Т е о р е м а 1 (теорема Пифагора). Если векторы x; y 2 H перпендикулярны, то имеет место равенство jjx + yjj2 = jjxjj2 + jjyjj2:
Доказательство. Из определения нормы и свойств скалярного произведения следуют равенства
jjx + yjj2 = (x + y; x + y) = (x; x) + (x; y) + (y; x) + (y; y) = jjxjj2 + jjyjj2:
Определение 4. Подмножество M из H называется ортонормированным, если выполнены условия: 1) jjxjj = 1 8x 2 M ; 2) (x; y) = 0 8 x; y 2 M; x 6= y:
Лемма 1. Пусть fe1; ; emg – конечное ортонормированное множе-
m |
|
|
|
|
m |
|
|
|
2 H вида |
iP |
|
ство из H . Тогда для любых двух векторов x; y |
x = iei; |
||||
iP |
|
|
|
|
=1 |
|
|
|
|
|
|
y = iei имеет место равенство |
|
|
|
|
|
=1 |
|
|
|
|
|
|
m |
|
|
||
|
Xi |
|
|
|
|
|
|
|
|
||
(x; y) = |
i i: |
|
|
||
|
=1 |
|
|
|
|
Доказательство. Используя свойства векторов из ортонормированного множества, получаем следующие равенства
(x; y) = |
m |
iei; |
m |
jej |
! = |
m |
( iei; iei) = |
m |
i i(ei; ei) = |
m |
i i: |
||||
|
X |
|
X |
|
|
X |
|
X |
|
|
|
Xi |
|
|
|
|
i=1 |
|
j=1 |
|
|
i=1 |
|
i=1 |
|
|
|
=1 |
|
|
|

106 Глава 3. Линейная алгебра
m
P
Следствие 1. Пусть x = iei – вектор из условий леммы 1. Тогда
i=1
m
jjxjj2 = P j ij2:
i=1
Следствие 2. Векторы из ортонормированного множества e1; ; en
линейно независимы.
n
P
Доказательство. Если iei = 0; то из следствия 1 получаем
i=1
n
0 = P j ij2:
i=1
Определение 5. Базис e1; ; em из евклидова пространства H называется ортонормированным, если векторы e1; ; em образуют ортонормированное множество.
Пример 6. Обычный базис e1 = (1; 0; ; 0); ; en = (0; 0; ; 1) из евклидова пространства Kn (пример 1) является ортонормированным.
Пример 7. Функция
ek(t) = p1w ei2wk t; k = 0; 1; ; n
образуют ортонормированный базис в подпространстве Tn;w из пространства Cw (см. пример 4).
Т е о р е м а 2. Пусть H – евклидово пространство и e1; ; en – ортонормированный базис в H , тогда для любого вектора x 2 H справедливо равенство
|
n |
|
|
Xi |
|
x = |
(x; ei)ei: |
|
|
=1 |
|
n |
n |
|
iP |
|
|
Доказательство. Пусть x = |
iei – разложение вектора x по базису |
|
|
=1 |
= k: |
e1; ; en . Тогда (x; ek) = P iei; ek |
||
i=1
Числа (x; ek); k = 1; ; n называются коэффициентами Фурье вектора
x.
Следствие. Любая функция ' из Tn;w представима в виде
|
|
|
|
n |
exp |
i |
2w t |
; t 2 R; |
|
|
|
'(t) = k= n 'k |
|||||
|
|
|
|
X |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
i2 wkt |
|
|
|
|
где 'k = |
1 |
R0 |
'(t) exp |
dt; n k n: Числа 'k; n k n |
||||
w |
||||||||
называются коэффициентами Фурье функции ':
