
Лекции по алгебре.Баскаков
.pdfx 17: Пространства со скалярным произведением. Евклидовы пространства |
107 |
Определение 6. Пусть M – подпространство из H . Вектор x 2 H
называется перпендикулярным (ортогональным) подпространству M (при этом используется обозначение x?M ), если x?m 8m 2 M: Совокупность всех векторов, перпендикулярных подпространству M , называется подпро-
странством (см. упражнение 7), ортогональным M и обозначается символом
M?.
Замечание 2. Если M – подпространство из H , то M TM? = f0g: Действительно, если x 2 M TM?; то (x; x) = 0; и поэтому x = 0:
Определение 7. Пусть M – подпространство из H . Вектор a 2 M называется ортогональной проекцией вектора x 2 H на M , если вектор x a перпендикулярен M (см.рис. 15).
Т е о р е м а 3. Пусть M – конечномерное подпространство из H и e1; ; en – ортонормированный базис в M . Тогда для любого вектора x 2 H вектор
n |
|
Xk |
|
x1 = (x; ek) ek |
(1) |
=1 |
|
является единственной ортогональной проекцией вектора x на M , причем имеет место равенство
|
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
jjxjj2 = |
X |
|
|
|
Xk |
(x; ek) ekjj2: |
|
|
||||
|
|
j (x; ek)j2 + jjx |
|
|
(2) |
|||||||||
|
|
|
|
k=1 |
|
|
|
=1 |
|
|
|
|
|
|
Доказательство. Непосредственно из определения |
проекции и |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
свойств скалярного произведения следует, что вектор x1 = |
kek из M |
|||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
M |
|
k=1 |
|
является ортогональной проекцией вектора |
на |
|
только тогда, |
|||||||||||
|
|
тогда иP |
|
|||||||||||
|
n |
kek; ej) = 0 |
|
|
|
|
|
|
|
|
|
|
||
когда x k=1 |
|
8 j = 1; : : : ; n |
или, что эквивалентно, вы- |
|||||||||||
|
|
n |
|
= (x; e |
); |
j = 1; |
|
; n: Следовательно, проекция x |
|
|||||
полняются |
равенства |
|
|
|
||||||||||
P |
|
j |
j |
|
|
|
|
|
|
|
|
|
1 |
|
имеет вид x1 = j=1 (x; ej) ej: Поскольку векторы x2 = x x1 и x1 перпен- |
|
другу, то из теоремы Пифагора и её следствия 1 следует, |
|
дикулярны другP |
|
что |
|
n |
n |
Xk |
X |
jjxjj2 = jjx1jj2 + jjx2jj2 = |
j (x; ek)j2 + jjx (x; ek)jj2: |
=1 |
k=1 |
Теорема доказана.
Следствие 1 (неравенство Бесселя). Если fe1; : : : ; eng – конечное ортонормированное множество из H; то для любого вектора x 2 H имеет

108 |
Глава 3. Линейная алгебра |
место неравенство Бесселя
n
X
j (x; ek)j2 jjxjj2 |
(3) |
k=1
(т.е. длина проекции вектора x не превосходит длины вектора x).
Следствие 2 (неравенство Шварца). Для любой пары векторов x; y 2 H имеет место неравенство Шварца
j(x; y)j jjxjj jjyjj:
Доказательство. Если y = 0, то доказываемое неравенство очевидно. Если y 6= 0; то, применяя к вектору x с использованием одноэлементного ортонормированного множества e1 = y=jjyjj; неравенство Бесселя (3), получим
j(x; e1)j2 = j(x; y=jjyjj)j2 jjxjj2;
откуда следует доказываемое неравенство.
Неравенство Шварца позволяет ввести понятие угла между двумя векторами x; y 2 H . А именно, угол 0 ' < определяется из равенства (при
K = R)
(x; y) cos ' = jjxjj jjyjj:
"Подсказкой"для такого определения служит пример 1.
Следствие 3 (неравенство Коши-Буняковского). Для любых двух наборов чисел x = (x1; : : : ; xn); y = (y1; : : : ; yn) 2 Kn имеет место неравенство
n |
|
n |
!1=2 n |
!1=2 |
X xi |
|
i |
|
|
|
X jxij2 |
|
|
|
|
X jyij2 |
|
: |
||||
y |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
i=1 |
|
|
|
|
|
|
i=1 |
|
|
|
|
||
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следствие 4. Для нормы jjxjj = |
|
|
|
в H выполнено условие 3), |
|||||||||||||
|
|
(x; x) |
|||||||||||||||
т.е. имеет место неравенство |
jj |
|
jj jj |
x |
jj |
|
jj jj |
8 |
x; y |
2 |
H: |
||||||
|
x + y |
|
p |
|
+ |
|
|
|
|
|
|
||||||
Доказательство. Используя неравенство Шварца получаем
kx + yk2 = (x + y; x = y) = kxk2 + (x; y) + (y; x) + kyk2 =
kxk2 + 2Re(x; y) + kyk2 kxk2 + 2kxkkyk + kyk2 = (kxk + kyk)2; x; y 2 H:
x 17: Пространства со скалярным произведением. Евклидовы пространства |
109 |
Следствие 5. Для любых комплексных чисел x1; : : : ; xn; y1; : : : ; yn имеет место неравенство
n |
jxi + yij2 !1=2 |
n |
jxij2 !1=2 + |
n |
jyij2 !1=2 : |
X |
|
Xi |
|
X |
|
i=1 |
|
=1 |
|
i=1 |
|
До сих пор нами не установлено существование ортонормированного базиса в евклидовом пространстве. В следующей теореме указывается способ построения ортонормированного базиса, исходя из некоторого заданного базиса.
Т е о р е м а 4 (процесс ортогонализации Грама-Шмидта). Пусть f1; : : : ; fn – линейно независимые векторы из H . Тогда векторы e1; : : : ; en; определенные следующими равенствами
e1 = g1=jjg1jj; g1 = f1;
e2 = g2=jjg2jj; g2 = f2 (f2; e1)e1;
e3 = g3=jjg3jj; g3 = f3 (f3; e2)e2 (f3; e1)e1;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
en = gn=jjgnjj; gn = fn (fn; en 1)en 1 (fn; e1)e1;
образуют ортонормированное множество в H . В частности, e1; : : : ; en – ортонормированный базис в H , если H конечномерно и f1; : : : ; fn – базис в
H .
Доказательство. Каждый из построенных векторов gk; k = 1; : : : ; n ненулевой (это следует из линейной независимости векторов f1; : : : ; fn ) и поэтому jjgkjj 6= 0 8 k = 1; : : : ; n: По определению, jjekjj = 1 8 k = 1; : : : ; n причем непосредственно из теоремы 3, являющейся основой для определения векторов g1; g2; : : : ; gn; следует их взаимная ортогональность и, следовательно, взаимно ортогональны векторы e1; : : : ; en: Из следствия 2 теоремы 1 следует их линейная независимость и, следовательно, в силу следствия 2 теоремы 2 из x 2 они образуют базис в H , если dim H = n:
Отметим, что использование теоремы 3 осуществляется следующим образом. Берется одномерное подпространство M1 H с ортонормированным базисом fe1g. Тогда (f2; e1)e1 проекция вектора f2 на M1 и, следовательно, g2 = f2 (f2; e1)e1 перпендикулярен M1 . Затем рассматривается двумерное подпространство M2 c с ортонормированным базисом fe1; e2g и тогда вектор g3 = (f3; e2)e2 + (f3; e1)e1 – проекция вектора f3 на M2 и, следовательно,
110 |
Глава 3. Линейная алгебра |
g3?M2 |
( в частности, g3?e1 и g3?e2 ). Аналогичным образом строятся век- |
торы g4; : : : ; gn: Теорема доказана.
Таким образом, в каждом евклидовом пространстве существует ортонормированный базис.
Пример 8. Рассмотрим базис '0(t) = 1; |
'1(t) = t; : : : ; 'n(t) = tn в ев- |
|||||||
клидовом |
1 |
пространстве |
Pn(R) |
со |
скалярным |
произведением |
||
(x; y) = |
1 |
x(t)y(t)dt: Этот базис не является ортонормированным. Резуль- |
||||||
татом |
указанной в теореме 4 процедуры ортогонализации являются много- |
|||||||
|
R |
|
|
|
|
|
|
|
члены Лежандра
p0 |
(t) = p2; pk(t) = p |
2kk! |
|
dtk (t2 |
1)k; k = 1; : : : ; n: |
|||
|
1 |
|
|
k + 1=2 |
dk |
|
||
|
|
|
|
|
|
|
|
|
Определение 8. Скажем, что пространство H является ортогональ-
L
ной прямой суммой своих подпространств H1 и H2 , если H = H1 H2 и x1?x2 8x1 2 H1; 8x2 2 H2:
Т е о р е м а 5. Пусть M – подпространство из евклидова пространства
H . Тогда H является ортогональной прямой суммой подпространств M и M?:
Доказательство. Пусть e1; : : : ; ek – ортонормированный базис в M . Тогда, согласно теореме 3, вектор x 2 M единственным образом представляется в виде x = x1 + x2 , где x1 2 M; x2 2 M? и x1 – проекция вектора x на
M .
Рассмотрим еще одно определение проекции вектора на подпространство, которое будет эквивалентно ранее введенному определению.
Определение 9. Вектор a из подпространства M линейного пространства H называется ортогональной проекцией вектора x 2 H на M , если для любого вектора m 2 M; m 6= a имеет место неравенство
jjx ajj < jjx mjj
(т.е. расстояние от вектора x до вектора a меньше расстояния от вектора x до любого отличного от a вектора m из M ).
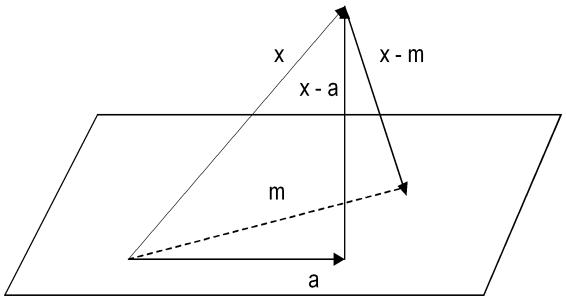
x 17: Пространства со скалярным произведением. Евклидовы пространства |
111 |
Рис. 15
Т е о р е м а 6. Оба определения ортогональной проекции эквивалент-
ны.
Доказательство. Пусть x1 2 M – ортогональная проекция вектора x на M в смысле определения 7 и m – произвольный вектор из M , отличный от x1 . Из равенства x m = x x1 + x1 m; где x1 m?x x1; применяя теорему Пифагора, получаем
jjx mjj2 = jjx x1jj2 + jjx1 mjj2 > jjx x1jj2:
Таким образом, x1 – проекция вектора x в смысле определения 9. Из этого же равенства следует, что если x1 - проекция вектора x на M в смысле определения 9, m = x1 - проекция x на M по определению 7 и x1 6= x01; то kx x01k < kx x1k: Получено противоречие. Теорема доказана.
Замечание 3. Непосредственно из определения 9 ортогональной проекции следует, что для любого вектора x 2 H его проекция a на подпространстве M H обладает свойством
|
|
|
|
|
jj |
x |
|
a |
jj = m M |
jj |
x |
|
jj |
|
|
|
|
|
|
|
|
|
inf |
|
|
m : |
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Величину |
inf |
jj |
x |
|
m |
|
|
|
|
|
|
|
|
x |
до подпро- |
m M |
|
jj называют расстоянием от вектора |
|
||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
странства M . Таким образом, для того чтобы найти это расстояние, достаточно найти проекцию a (например, использовать теорему 3 в случае конечномерного подпространства M ) и вычислить длину вектора x a:
112 |
Глава 3. Линейная алгебра |
Упражнения к § 17
1. Докажите |
следующие |
свойства |
скалярного |
произведения: |
||
20) (x; y + z) = (x; y) + (x; z); 30) (x; y) = |
|
(x; y): |
|
|||
|
|
|||||
2.Пусть z1; : : : ; zm – различные комплексные числа. Докажите, что в линейном пространстве Pn(C); где n < m формула
m
X
(f; g) = f(zk) g(zk); f; g 2 Pn(C)
k=1
задает скалярное произведение. Верно ли это утверждение для m n?
3.Какие из следующих отображений fi : C2 C2 ! C; i = 1; 2; 3; 4 задают скалярное произведение в C2 :
a) f1(x; y) = x1y2 + x2y2 ; b) f2(x; y) = x1y1 ;
c) f3(x; y) = x1y2 + x2y1 ; d) f4(x; y) = 5x1y1 + 3x2y2 ?
4.Докажите, что в пространстве H со скалярным произведением для любой пары векторов x; y 2 H имеет место тождество параллелограмма
kx + yk2 + kx yk2 = 2(kxk2 + kyk2):
5. Докажите, что множество |
|
p ; |
p ; : : : ; |
p ; |
p ; : : : |
|||||
S = |
p2 ; |
p |
; |
p |
; |
|||||
|
1 |
|
cos |
t |
sin t |
cos 2t |
sin 2t |
cos nt |
sin nt |
|
образует ортонормированное множество в линейном пространстве C2 (см. пример 4).
6. Докажите, что функции
1 |
|
cos |
t |
sin t |
|
cos nt |
|
sin nt |
||||||||
p |
|
; |
p |
|
; |
p |
|
|
; : : : ; |
p |
|
|
; |
p |
|
|
2 |
|
|
2 |
2 |
||||||||||||
образуют ортонормированный базис в подпространстве Tn;2 из C2 (см. пример 4).
7.Пусть H - линейное пространство со скалярным произведением и M - подмножество из H . Докажите, что множество M? образует линейное
подпространство из H .

x 17: Пространства со скалярным произведением. Евклидовы пространства |
113 |
8.Докажите, что если j(x; y)j = kxkkyk; x; y 2 H; то векторы x и y линейно зависимы.
9. Докажите, что векторы x; y 2 H равны тогда и только тогда, когда
(x; a) = (y; a) 8a 2 H:
10.Докажите, что в пространстве C[a; b] (см. пример 3) угол между векторами (функциями) fn(t) = tn; fn+1(t) = tn+1 стремится к нулю при n ! 1.
11. Вычислите угол между функциями ' и из пространства C[0; 2 ] (см. пример 3), если
a) '(t) = t; (t) = 1; b) '(t) = t; (t) = sin t:
12.Пусть e1; : : : ; en – базис из евклидова пространства H , обладающий свойством (ei; ej) = 0 для i 6= j . Докажите, что для любого вектора x 2 H имеют место равенства
n
x =
X (x; ek)
(ek; ek)
k=1
e ; |
x 2 = |
n |
j(x; ek)j2 |
: |
|||
|
|||||||
k |
k k |
Xk k |
ek |
k |
2 |
|
|
|
|
=1 |
|
|
|
|
|
13.Осуществите в евклидовом пространстве R3 процесс ортогонализации для следующих векторов
1) x1 = (2; 2; 1); x2 = (3; 4; 1); x3 = (1; 3; 1);
2)x1 = (1; 2; 2); x2 = ( 1; 0; 1); x3 = (5; 3; 7):
14.Проверьте, что следующие совокупности векторов образуют ортонормированные множества из R3 и дополните их до ортонормированных базисов
1) x1 = |
|
11 |
; |
2 |
|
2 |
; |
x2 = |
|
2 |
; |
14 |
; |
1 |
; |
|
15p; |
|
|
|
|
||||||||||
15 |
3 |
15 |
15 |
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2)x1 = 12; 12; 2 :
15.В пространстве Pn(R) определите скалярное произведение так, чтобы многочлены '0(t) = 1; '1(t) = t; : : : ; 'n(t) = tn образовывали ортонормированный базис.
16.Найдите какой-нибудь ортонормированный базис в каждом из следующих подпространств евклидова пространства R3
1)M1 = fx = (x1; x2; x3) 2 R3; x1 + x2 = 0g;
2)M2 = fx 2 R3; x1 + x2 x3 = 0g.2

114 |
Глава 3. Линейная алгебра |
17.Найдите ортонормированный базис в ортогональном дополнении к следующим подпространствам из евклидова пространства R4 :
1)подпространству M , являющемуся линейной комбинацией векторов x = (1; 1; 1; 1); y = (1; 1; 1; 1);
2)подпространству M = f( ; ; ; ) : 2 Rg:
18.Найдите проекцию многочлена '(z) = z2 из P2(C) на подпространство
1
R
P1(C) ((x; y) = x(t) y(t)dt; x; y 2 P2(C)):
1
19. В евклидовом пространстве P2(R) (со скалярным произведением
1
R
(x; y) = x(t)y(t)dt найдите ортонормированный базис.
0
20.Найдите расстояние от вектора a = (1; 1; 1) 2 R3 до подпространства
M = fx = (x1; x2; x3) 2 R3 : x1 + x2 + x3 = 0g:
21.Углом между вектором x 2 H и подпространством M из H называется точная нижняя грань значений угла, который образует вектор x с ненулевыми векторами из M .
Докажите, что угол между вектором x 2 H и конечномерным подпространством M H равен углу между вектором x и его проекцией на M .
22.Докажите, что углы, которые вектор x 2 H образует с произвольным подпространством M из H и его ортогональным дополнением, в сумме равны =2:
23.Найдите угол между вектором x = ( 3; 15; 1; 5) 2 R4 и подпространством M , являющимся линейной оболочкой векторов
|
x1 = (2; 3; 4; 6); x2 = (1; 8; 2; 16); x3 = (1; 5; 2; 10): |
|||||||||
24. |
В пространстве C[0; 1] со скалярным произведением |
|||||||||
|
1 |
( ); k = 0; 1; 2: |
|
|
|
|||||
|
R0 |
|
|
|
||||||
|
(x; y) = |
x(t) y(t)dt найдите проекцию функции '(t) = t3 на каждое |
||||||||
|
из подпространств Pk R |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
p |
|
|
|
|
|
2dx: |
25. |
|
inf |
R0 |
x |
|
ax |
|
b |
||
Вычислите величину a;b2R |
( |
|
|
) |
|
|||||
x 18: Пространство линейных операторов |
115 |
26. В пространстве многочленов P(R) со скалярным произведением (f; g) =
1
=f(x)g(x)dx найти расстояние от многочлена xn до подпространстваR
1
Pn 1(R):
27. Докажите, что на линейном пространстве матриц Matrm;n(K) формула
P |
|
|
|
|
|
|
(A; B) = |
aijbij; где A = (fij); B |
= (bij) 2 |
Matrn(K) определяет |
|||
ij |
|
|
|
|
|
|
скалярное произведение, при этом kABk kAkkBk A B 2 |
n |
|||||
x 18. Пространство линейных операторов
В этом параграфе мы вводим и начинаем изучение гомоморфизмов линейных пространств, называемых линейными операторами (понятие гомоморфизмов других алгебраических объектов рассматривалось в x 7).
Определение 1. Пусть X и Y – два линейных пространства, рассматриваемых над одним и тем же полем K . Отображение A : X ! Y называется линейным оператором, если выполнены следующие два условия:
1)A(x1 + x2) = A(x1) + A(x2) (свойство аддитивности);
2)A( x) = A(x) (свойство однородности)
для любых x; x1; x2 2 X и 2 K:
Ясно, что линейность отображения A : X ! Y эквивалентна выполнению условия A( x1 + x2) = A(x1) + A(x2) 8 ; 2 K 8x1; x2 2 X .
Значение линейного оператора A на каждом векторе x обозначается, как правило, символом Ax (вместо A(x)). Множество линейных операторов, определенных на X со значениями в Y , обозначается символом L(X; Y ). Полагается L(X) = L(X; Y ) для X = Y . Отображение f : X ! X вида f(x) = Ax + b; где A 2 L(X) и b 2 X; назовем аффинным преобразованием.
Замечание 1. Свойство аддитивности линейного оператора A означает, что он является гомоморфизмом абелевых групп X и Y .
Замечание 2. Из свойства однородности следует, что A0 = A(0 0) = 0A(0) = 0; т.е. нулевой вектор пространства X переходит в нулевой вектор пространства Y .
Замечание 3. Требование, чтобы линейные пространства X и Y рассматривались над одним полем K , связано с корректностью формулировки свойства однородности.
Определение 2. Линейный оператор A : X ! Y называется линейным функционалом, если Y = K; где K – поле, над которым рассматривается пространство X . Функционал называется вещественным, если K = R и –
комплексным, если K = C:

116 Глава 3. Линейная алгебра
Множество линейных функционалов L(X; K) обозначается символом
X и называется сопряженным к X пространством.
Рассмотрим несколько примеров линейных операторов (функционалов). Пример 1. Пусть X = Y = Pn(K) (либо X = Y = Tn;w ). Рассмотрим
отображение D : X ! X; определенное формулой
D' = '0;
называемое оператором дифференцирования. Свойства аддитивности и однородности следуют из обычных свойств производной.
Пример 2. Пусть X = Y = C[a; b]: Отображение J : C[a; b] ! C[a; b];
определенное формулой
(J')(t) = Z |
t |
'(s)ds; ' 2 C[a; b]; t 2 [a; b]; |
|
a |
|
является линейным оператором; он называется оператором интегрирования. Его линейность обеспечивается известными свойствами интеграла.
Пример 3. Пусть X = Pn(K) (или X = C[a; b]). Отображение ' : X ! K; определенное формулой
b
Z
'(x) = x(s)ds; x 2 X;
a
является линейным функционалом.
Пример 4. Пусть H – пространство со скалярным произведением над полем K и a – некоторый вектор из H . Тогда из свойств скалярного произведения следует, что отображение ' : H ! K; определенное формулой
'(x) = (x; a); x 2 H;
является линейным функционалом.
Вчастности, для любого вектора a = ( 1; : : : ; n) 2 Cn (см. пример 2 из x 4) отображение ' : X ! K; определенное формулой
n
X
'(x) = (x; a) = ixi; x = (x1; : : : ; xn) 2 Kn;
i=1
является линейным функционалом. Позже мы убедимся (следствие 2 теоремы 1), что любой линейный функционал ' : Cn ! C имеет именно такой вид.
Пример 5. Пусть M – конечномерное подпространство из пространства со скалярным произведением H . Тогда отображение P = PM : H ! H;
