
Лекции по алгебре.Баскаков
.pdf
27
ГЛАВА 2. АЛГЕБРАИЧЕСКИЕ ОБЪЕКТЫ; АЛГЕБРА МНОГОЧЛЕНОВ
В данном разделе рассматриваются множества, над элементами которых можно производить определенные алгебраические операции. В зависимости от тех или иных свойств алгебраических операций и числа операций производится классификация таких множеств (алгебраических структур). Возникают такие алгебраические структуры как группы, кольца, тела, поля. Типичными примерами являются множества R и Z; в которых введены две алгебраические операции сложения и умножения чисел.
x 5. Алгебраические операции. Группы
Определение 1. Пусть S – непустое множество. Говорят, что на S задан внутренний закон композиции или алгебраическая операция, если задано отображение ' : S S ! S; т.е. каждый паре элементов a; b из S ставится по некоторому правилу вполне определенный элемент из S .
Временно элемент '(x; y) обозначим символом x'y; однако сразу отметим, что наиболее распространена так называемая мультипликативная запись и терминология. Элементы x; y, над которыми совершается алгебраическое действие, пишутся рядом без какого–либо знака между ними или же между ними ставятся знаки ; : '(x; y) = xy; '(x; y) = x y; '(x; y) = x y: В этом случае элементы x и y называются сомножителями (x – левый сомножитель, y – правый), а элемент '(x; y) – их произведением.
Определение 2. Элементы x и y из S называются перестановочными (коммутирующими) относительно закона композиции ' : S S ! S , если выполнено равенство x'y = y'x:
Часто употребляется (особенно в случае, когда каждая пара элементов из S перестановочна относительно ') аддитивная форма записи и терминология. В этом случае элемент '(x; y) обозначается символом x + y, который называется суммой, а x и y – слагаемыми.
Для конкретных множеств названия определенных алгебраических действий закреплены установленными правилами (сложения, умножения) и употребляются без особых оговорок (например, для R и Z):
Определение 3. Закон композиции ' : S S ! S называется ассоциативным, если для любых трех элементов a; b; c из S имеет место равенство
a'(b'c) = (a'b)'c
28 |
Глава 2. Алгебраические объекты; Алгебра многочленов |
(a(bc) = (ab)c в мультипликативной форме записи или a+(b+c) = (a+b)+c
– в аддитивной).
Рассмотрим несколько примеров внутренних законов композиции (алгебраических операций).
Пример 1. Пусть S = R; '1(x; y) = xy (xy – обычное произведение чисел), '2(x; y) = x + y (обычное сложение чисел). Таким образом, на R заданы два внутренних ассоциативных закона композиции.
Пример 2. Отображение ' : N N ! N; '(n; m) = nm задает внутренний закон композиции на множестве натуральных чисел N: Однако эта алгебраическая операция не ассоциативна, поскольку n'(m'k) = = nmk 6= (n'm)'k = (nm)k = nmk для некоторых n; m; k. Например, при n = 2; m = 2; k = 3:
Пример 3. Пусть X – некоторое множество и F(X) – множество всех отображений множества X в X . Определим отображение
: F(X) F(X) ! F(X)
следующим равенством
(f; g) = f g;
где f g – суперпозиция отображений f; g 2 F(X): Таким образом, на F(X) задан внутренний закон композиции, который ассоциативен в силу теоремы 2 из x 3:
Пример 4. Пусть S - совокупность всех подмножеств данного множества X . Рассмотрим отображения f; '; : S S ! S вида f(A; B) = A B;
T |
S |
'(A; B) = A B; (A; B) = A |
B: Таким образом, на S определены три |
алгебраические операции. Из свойств 1, 2 и 8 (см. §1) следует, что все три операции ассоциативны.
Множество вместе с заданными на этом множестве алгебраическими операциями (их может быть несколько) называют алгебраической структурой.
Существует много различных алгебраических операций на данном множестве, но большинство полезных алгебраических структур (т.е. структур, которые описывают естественно возникающие явления и пригодны для вычислений) можно разбить на небольшое число типов.
Одним из наиболее важных типов алгебраических структур является группа.
Определение 4. Множество G называется группой, если задан закон композиции ' : G G ! G (элемент x ' y = '(x; y) далее обозначается символом xy и называется произведением элементов x и y (т.е. используется мультипликативная терминология), обладающий свойствами:
x 5: Алгебраические операции.Группы |
29 |
1) закон композиции ' ассоциативен (т.е. x(yz) = |
(xy)z для всех |
x; y; z 2 G); |
|
2)в G есть элемент e, называемый единицей, со свойствами xe = ex = x
8x 2 G;
3)для всякого элемента x 2 G cуществует элемент y 2 G такой, что
xy = yx = e. Элемент y называется обратным к x и обозначается символом x 1 .
Определение 5. Группа G называется абелевой (в честь норвежского математика Н.Г.Абеля (1802-1829)), если любые два элемента группы G перестановочны относительно введенного закона композиции.
Важно отметить, что именно в абелевой группе наиболее часто вместо мультипликативной записи и терминологии используется аддитивная форма записи и терминология. Произведение xy элементов x; y 2 G записывают в виде x+y. Единица e группы обозначается символом 0 и называется нулевым элементом. Элемент x 1 , обратный к элементу x из G, называется противоположным к x и обозначается символом x (таким образом, x + ( x) = 0:)
Рассмотрим примеры групп.
Пример 5. Группа R вещественных чисел с внутренним законом композиции, определяемым сложением чисел (с аддитивной формой записи алгебраической операции; роль единицы играет число 0, а обратным к каждому элементу x 2 R служит число - x).
Пример 6. Множество R+ всех положительных чисел с законом композиции, определяемым умножением чисел, является группой. Единицей группы служит число 1. Обратным к каждому числу x 2 R+ является число
1=x:
Обе группы R и R+ абелевы. Отметим, что деление в R+ является неассоциативной алгебраической операцией.
Пример 7. Двухэлементное множество Go = f 1; 1g, состоящее из двух чисел 1 и -1, является абелевой группой (алгебраическая операция задается обычным умножением чисел).
Пример 8. Множество V 3 свободных векторов пространства является абелевой группой (относительно обычной операции сложения векторов).
Пример 9. Множество Rn всех упорядоченных наборов n вещественных чисел является абелевой группой. Используя аддитивную форму записи, алгебраическую операцию зададим формулой
x + y = (x1 + y1; x2 + y2; : : : ; xn + yn);
где x = (x1; : : : ; xn); y = (y1; : : : ; yn) 2 Rn: Нулевым элементом служит набор чисел 0 = (0; : : : ; 0). Элементом, противоположным к x служит элемент
30 |
Глава 2. Алгебраические объекты; Алгебра многочленов |
x = ( x1; : : : ; xn):
Пример 8. Пусть X – непустое множество. Через S(X) обозначим множество всех биективных отображений множества X в X . Таким образом, S(X) – подмножество из множества всевозможных отображений F(X), на котором задан ассоциативный закон композиции, определяемый суперпозицией отображений. Поскольку суперпозиция биективных отображений является снова биективным отображением (см. теорему 3 из x 3), то указанный закон композиции определен также на S(X); S(X) – группа относительно суперпозиции отображений. Роль единицы группы S(X) играет тождественное отображение и обратным к каждому отображению f 2 S(X) служит обратное отображение f 1 (см. определение 10 и упражнение 13 из x 3).
Обратим внимание на то, что группа S(X) не является абелевой, если X содержит более двух элементов (см. пример 9).
Определение 6. Пусть X – конечное множество. Элементы группы S(X) называют перестановками множества X (таким образом, перестановка
– биективное отображение конечного множества).
Перестановку ' множества A = fa1; : : : ; ang часто будем записывать в
виде (ak1 ; ak2 ; : : : akn), где ak1 = '(a1); ak2 = '(a2); : : : akn = '(an):
Перестановку множества A = f1; : : : ; ng удобно задавать в виде таблицы (это мы делали и будем делать далее).
k1 |
k2 |
: : : |
kn |
1 |
2 |
: : : |
n |
или, короче,
(k1; : : : ; kn);
где k1; : : : ; kn – различные числа из A: Соответствующее отображение f : A ! A определяется равенствами f(j) = kj; j = 1; : : : ; n.
Если X = f1; : : : ; ng, то группу перестановок S(X) обозначим символом
Sn ; ее называют симметрической группой степени n:
Пример 9. Группа Sn не является абелевой, если n 3: Например, для
перестановок |
|
|
|
|
|
n |
|
|
3 |
|
|
|
|
|
n |
|
f = |
3 |
1 |
2 |
4 |
5 |
: : : |
; |
g = |
2 |
1 |
4 |
5 |
: : : |
|||
|
1 |
2 |
3 |
4 |
5 |
: : : |
n |
|
|
1 |
2 |
3 |
4 |
5 |
: : : |
n |
получаем
x 5: Алгебраические операции.Группы |
31 |
f g = 2 |
1 |
3 |
4 |
5 |
: : : |
n ; g f = |
1 |
3 |
2 |
4 |
5 |
: : : |
n : |
1 |
2 |
3 |
4 |
5 |
: : : |
n |
1 |
2 |
3 |
4 |
5 |
: : : |
n |
Пример 10. Двухэлементное множество |
f0; 1g образует |
абелеву |
|||||||||||
группу с операцией |
сложения, определяемой |
равенствами: |
0 |
+ 0 = 0; |
|||||||||
0 + 1 = 1; 1 + 1 = 0. |
|
|
|
|
|
|
|
|
|
|
|
||
Определение 7. Подмножество G0 из группы G называется подгруппой, если вместе с каждой парой элементов x; y 2 G0 элементы x 1; xy также принадлежат G0 .
Непосредственно из определения следует, что G0 является самостоятельной группой. Отметим, что группа из примера 6 является подгруппой группы R: Множества Z и Q являются подгруппами группы R.
Определение 8. Отображение f : E ! E (где E – прямая либо плоскость, либо пространство) называется движением в E , если оно биективно, сохраняет расстояние между точками, т.е. расстояние dist(x; y) между двумя точками x и y из E совпадает с расстоянием dist(f(x); f(y)) между точками f(x) и f(y). Множество всех движений обозначим символом S0(E):
Пример 11. Множество движений S0(E) является подгруппой группы S(E). Единица IX группы S(E) является движением и поэтому принадлежит S0(E). Из определения движения следует, что если f и g – движения, то отображения f 1 и f g являются движениями (см.задачу 13).
Всякое преобразование (прямой, плоскости или пространства), которое является результатом некоторого механического перемещения, является движением (такие движения называются движениями первого рода). Отражение плоскости относительно прямой является движением, но не является движением первого рода. Все движения в E исчерпываются указанными выше отображениями.
Определение 9. Пусть F – некоторая фигура в E . Самосовмещением фигуры F в E называется движение в E , преобразующее фигуру F в себя.
Нетрудно показать (см. упражнение 10 к x 5), что множество всех самосовмещений фигуры F в E образует подгруппу группы движений в E . Группа самосовмещений фигуры характеризует степень "симметричности"фигуры. Чем больше число элементов группы самосовмещений, тем симметричней фигура. Так, например, четверка имеет группу самосовмещений, состоящую только из одного элемента (тождественного отображения). Окружность имеет группу самосовмещений, совпадающую с группой вращений плоскости вокруг центра этой окружности.
Пример 12. Рассмотрим группу самосовмещений правильного
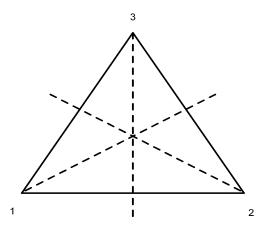
32 |
Глава 2. Алгебраические объекты; Алгебра многочленов |
Рис. 9
треугольника, вершины которого занумерованы числами 1,2,3. Каждое самосовмещение этого треугольника можно характеризовать перестановкой
1 2 3 k1 k2 k3
на множестве вершин треугольника. Здесь kj – номер места, которое после преобразования ' заняла вершина j; j = 1; 2; 3: Повороты '0 = e; '1; '2 плоскости на углы 0; 2=3 ; 4=3 соответственно вокруг точки 0 против часовой стрелки переводят треугольник в себя. Кроме того, имеется три осевых симметрии '3; '4; '5; определяемые осями симметрии a; b; c соответственно, проходящими через вершины треугольника и середины его противоположных сторон. В результате такого соответствия между самосовмещениями треугольника и перестановками множества вершин получаем
'0 |
|
1 |
2 |
3 |
; |
'1 |
2 |
3 |
1 |
; |
'2 |
3 |
1 |
2 |
; |
|
|
1 |
2 |
3 |
|
'4 |
1 |
2 |
3 |
|
'5 |
1 |
2 |
3 |
|
'3 |
|
1 |
3 |
2 |
; |
3 |
2 |
1 |
; |
2 |
1 |
3 |
: |
||
|
|
1 |
2 |
3 |
|
|
1 |
2 |
3 |
|
|
1 |
2 |
3 |
|
Таким образом, построен изоморфизм между группой самосовмещений и группой S3 (см. определение 12).
Определение 10. Подгруппа H из группы G называется нормальной, если a x a 1 2 H 8a 2 G 8x 2 H:
Непосредственно из определения следует, что каждая подгруппа из абелевой группы нормальна.
Пусть H – нормальная подгруппа группы G. На G введем отношение эквивалентности R, считая x y, если x y 1 2 H:
Лемма 1. R – отношение эквивалентности на G.
x 5: Алгебраические операции.Группы |
33 |
Доказательство. Очевидно, что x x 8x 2 G.
Если x y, то xy 1 2 H , и поэтому принадлежит H также элемент yx 1 = (xy 1) 1 (элемент yx 1 является обратным к xy 1 ). Итак, y x.
Наконец, если x y и y z, то xy 1; yz 1 2 H и поэтому xz 1 = = (xy 1)(yz 1) 2 H , что означает x z. Лемма доказана.
Лемма 2. Каждый класс эквивалентности A из фактор-множества G=R имеет вид xH = fxh : h 2 Hg, где x – любой элемент из A.
Доказательство. Пусть x – произвольный элемент из A. Если z = = xh 2 xH , то zx 1 = xhx 1 2 H , т.е. z 2 A. Следовательно, xH A. Обратно, если a 2 A, то x 1a = a 1(ax 1)a = h 2 H; т.е. a = xh 2 xH и поэтому A xH: Итак, A = xH 8x 2 A: Лемма доказана.
В фактор-множестве G=R введем операцию умножения, положив
AB = xyH , если A = xH и B = yH . Отметим, что AB = (x1H)(y1H);
8x1 2 A 8y1 2 B; так как xy x1y1 (ибо (x1y1)(xy) 1 = x1y1y 1x 1 = = (x1(y1y 1)x1 1(x1x 1) 2 H):
Непосредственно из ассоциативности операции умножения в группе G следует ассоциативность введенной операции умножения в фактор-мно- жестве G=R. Единицей в G=R является класс эквивалентности eH = H: Ясно, что класс эквивалентности x 1H является обратным к xH . Итак, G=R
– группа.
Определение 11. Группа G=R называется фактор-группой группы G по нормальной подгруппе H . Для полученной фактор-группы далее используется обозначение G=H:
Пример 13. Рассмотрим группу Z целых чисел (по сложению), некоторое натуральное число m 2 и подгруппу mZ целых чисел, делящихся на m. Подгруппа mZ приводит к отношению эквивалентности, рассмотренному в примере 2 из x 2: Тогда фактор-группа Zm = Z=mZ состоит из m классов эквивалентности.
mZ; 1 + mZ; : : : m 1 + Z;
где k + mZ = fk + mj; j 2 Zg; k = 1; 2; : : : ; m 1: При m = 2 получим, что группа Z2 состоит из двух элементов: класса 2Z = 0 + 2Z четных чисел и класса 1 + 2Z нечетных чисел. По определению 2Z + 2Z = 2Z; 2Z + (1 + 2Z) = 1 + 2Z; 1 + 2Z + (1 + 2Z) = 2Z:
Определение 12. Пусть G и S – две группы. Отображение f : G ! S
называется гомоморфизмом групп, если
f(g1g2) = f(g1)f(g2) 8g1; g2 2 G:
Если гомоморфизм f является биективным отображением, то он называется
изоморфизмом, а группы G и S – изоморфными.

34 Глава 2. Алгебраические объекты; Алгебра многочленов
Лемма 3. Если f : G ! S – изоморфизм групп, то обратное отображение f 1 : G ! S является гоморфизмом групп (и, следовательно, изоморфизмом).
Доказательство. Пусть s1; s2 – два элемента из группы S и g1; g2 – та-
кие элементы из G, что f(g1) = s1; f(g2) = s2: Тогда f(g1g2) = f(g1)f(g2) = = s1s2; и поэтому f 1(s1s2) = g1g2 = f 1(s1)f 1(s2) по определению обрат-
ного отображения. Лемма доказана.
Пример 14. Рассмотрим две группы: группу R (см. пример 4) и группу R+ (см. пример 5). Отображение f : R ! R+; определенное равен-
ством f(t) = exp |
t = et; t 2 R является изоморфизмом групп, так как |
f(t1 + t2) = et1+t2 |
= et1 et2 = f(t1)f(t2): Обратное отображение имеет вид |
f 1(t) = ln t 2 R+: Таким образом, R и R+ – изоморфные группы. Если взять какую-нибудь группу и рассмотреть изоморфные ей
группы, то нетрудно понять, что они алгебраически все одинаковы (могут отличаться природой элементов и групповыми операциями). Изоморфные группы, если их рассматривать как абстрактные группы, совпадают. Именно понятие изоморфизма групп позволяют отвлечься от природы элементов рассматриваемых групп, сосредоточившись на изучении алгебраической операции.
Пример 15. Группа Z2 (из примера 13) изоморфна группе f0; 1g (из примера 10). Изоморфизм f : Z2 ! f0; 1g задается с помощью двух равенств f(2Z) = 0 и f(1 + 2Z) = 1:
Определение 13. Пусть f : G ! S – гомоморфизм групп. Множество Ker f = fg 2 G : f(g) = eSg (eS – единица группы S ) называется ядром гомоморфизма f .
Т е о р е м а. Пусть f : G ! S – гомоморфизм групп. Тогда имеют место следующие свойства:
1) f(eG) = eS; 2) f(x 1) = f(x) 1 8x 2 G;
3) Ker f – нормальная подгруппа группы G.
Доказательство. 1. Пусть f(eG) = u: Тогда u = f(eG) = f(eGeG) = = f(eG)f(eG) = u2: Умножая обе части полученного равенства на элемент u 1 , получим, что u = eS .
2.Из равенств eS = f(eG) = f(xx 1) = f(x 1)f(x) следует, что f(x 1) = f(x) 1:
3.Если x 2 Ker f; т.е. если f(x) = eS , то из утверждения 2) полу-
чаем, что f(x 1) = f(x) 1 = eS; т.е. x 1 2 Ker f: Если x; y 2 Ker f;
то f(xy) = f(x)f(y) = e2S = eS: Таким образом, Ker f – подгруппа из группы G. Подгруппа Ker f является нормальной, так как f(g x g 1) = = f(g)f(x)f(g 1) = es 8g 2 G 8x 2 Ker f: Теорема доказана.
x 5: Алгебраические операции.Группы |
35 |
В заключение параграфа отметим, что в дальнейшем для произведения (суммы в абелевой группе) нескольких элементов из группы используются следующие обозначения
n |
n раз |
||||
Yj |
|||||
aj = a1a2 |
: : : an; an = a : : : a ; a n = (a 1)n ; |
||||
=1 |
| |
|
{z |
|
} |
|
|
|
|
|
|
n
X
aj = a1 + + an
j=1
(если G – абелева группа с аддитивной формой записи операции). Используется также обозначение
X
aj
j2M
для суммы элементов aj; j 2 M из абелевой группы G, индексированных элементами конечного множества M .
Упражнения к § 5
1. Определите, какие из следующих числовых множеств образуют группу
а) по сложению, |
б) по умножению |
1) Q; 2)R n f0g; |
3)R+ Sf0g; 4)f1; 1g; 5)f2; : : : 2n; : : : g: |
2.Докажите, что следующие множества образуют группы относительно введенных на них операций умножения
1)множество свободных векторов (с операцией сложения векторов);
2)повороты плоскости вокруг заданной точки с операцией суперпозиции отображений (поворотов);
3)движения плоскости, оставляющие некоторый треугольник на ме-
сте;
4)множество непрерывных биективных отображений отрезка
[0; 1] в себя, принимающих нулевое значение в точке 0 и равных 1 в точке 1 (с операцией суперпозиций функций).
5) множество корней n-ой степени из единицы с операцией умножения чисел.
3. Какие группы из предыдущей задачи абелевы?
36 |
Глава 2. Алгебраические объекты; Алгебра многочленов |
4.Докажите, что подмножество f(a; b) 2 R2 : a 6= 0g R2 образует группу относительно умножения, определяемого формулой
(a; b)(c; d) = (ac; ad + b):
Будет ли эта группа абелева?
5.Докажите, что функция вида f(x) = ax + b; a 6= 0; f : R ! R образуют группу относительно суперпозиции отображений, изоморфную группе из предыдущей задачи.
6.Докажите, что в любой группе
1)единичный элемент e единствен;
2)для любого элемента a обратный элемент a 1 единствен;
3)равенство ax = b равносильно x = a 1b, а равенство xa = b равносильно x = ba 1 ;
4) для любых двух элементов a; b выполняется равенство (ab) 1 =
= b 1a 1:
7.Докажите, что если квадрат любого элемента группы равен единичному элементу , то группа абелева.
8.Докажите, что множество перестановок
G1 = ff 2 Sn : f(1) = 1g
образует подгруппу, которая не является нормальной, если n 3.
9.Докажите, что множество параллельных переносов плоскости является нормальной подгруппой группы движений плоскости.
10.Докажите, что множество самосовмещений некоторой фигуры из (плоскости или пространства) E образует подгруппу группы движений в E .
11.Найдите подгруппу S всех самосовмещений прямой в группе всех движений плоскости. Докажите, что G – бесконечная неабелева группа.
12.Найдите подгруппу всех самосовмещений каждой из следующих фигур в группе всех движений плоскости:
а) ромба; б) квадрата; в) равнобедренного треугольника; г) правильного n –угольника; д) цифры 8.
