
Лекции по алгебре.Баскаков
.pdfx 12: Приближенное вычисление корней многочленов |
77 |
Следовательно, построенная таким способом система многочленов
f0(= f); f0; : : : ; fk = c
удовлетворяет условию 2) определения 1.
Рассматривая условие 1), допустим, что соседние многочлены fm и fm+1 имеют общий корень . Тогда из равенства (3) следует, что – корень многочлена fm 1 . Из равенства fm 2 = fm 1qm 1 fm получаем, что fm 2( ) = 0: Продолжая эти рассуждения, получим, что – общий корень для f и f0 , что противоречит простоте корня .
Наконец, выполнение условия 3) следует из равенства (3): если fm( ) = 0, то fm 1( ) = fm+1( ): Лемма доказана.
Определение 2. Пусть f0; f1; : : : ; fk – некоторая система Штурма для многочлена f . Если c 2 R и f(c) 6= 0; то рассмотрим упорядоченный набор чисел
f0(c) = f(c); f1(c); : : : ; fk(c)
вещественных чисел, и вычеркнем из него все числа, равные нулю. Число перемен знаков в оставшемся наборе чисел назовем числом перемен знаков в системе Штурма для многочлена f в точке x = c и это число обозначим
символом S(c) (таким образом, определено отображение S : R ! N |
f0g): |
|
Т е о р е м а (теорема Штурма). Пусть вещественные |
числа a; b |
|
|
S |
|
(a < b) не являются корнями многочлена f с вещественными коэффициентами и не имеющего кратных корней. Тогда S(a) S(b) и разность S(a) S(b) равна числу вещественных корней многочлена f , заключенных между a и b.
Доказательство. Покажем, что заданная в определении 2 функция
S
S : R ! N f0g); является невозрастающей. Пока аргумент x; возрастая, не совпадает с некоторым корнем одного из многочленов Штурма, знаки многочленов системы Штурма не будут меняться, и поэтому функция S будет постоянной на таких интервалах.
Имея в виду условие 2 из определения 1, остается рассмотреть два случая: 1) переход x через корень одного из промежуточных многочленов Штурма f1; f2; : : : ; fk 1 и 2) переход x через корень самого многочлена f .
Допустим, что x0 – корень одного из промежуточных многочленов fm; 1 m k 1: Тогда, согласно условию 3), числа fm 1(x0) и fm+1(x0) имеют противоположные знаки. Ввиду непрерывности многочленов можно указать интервал (x0 ; x0 + ) такой, что числа fk 1(x); fk+1(x); x 2 (x0; x0 + ) отличны от нуля и имеют противоположные знаки. Отсюда следует, что число перемен знаков в наборе чисел
fk 1(x); fk(x); fk 1(x)

78 Глава 2. Алгебраические объекты; Алгебра многочленов
не меняется для всех x 2 (x0 ; x0 + ): Это приводит к тому, что в системе Штурма перемены знака могут лишь перемещаться (но не возникают вновь и не исчезают). Поэтому число S(x) при переходе через число x0 не меняется.
Пусть теперь x0 – корень многочлена f . По условию 1 (из определения 2) число x0 не будет корнем для f1 . Следовательно, f1 6= 0 на некотором отрезке (x0 ; x0 + ); и поэтому f1 имеет на нем постоянный знак, для определенности пусть положительный. Тогда по свойству 4) сам многочлен f при переходе через точку x0 меняет знак с минуса на плюс, т.е. f(x0) < 0; f(x0 + ) > 0: Тогда для двух наборов чисел f(x0 ); f1(x0 + ) и f(x0 ); f1(x0 + ) соответствующие системы знаков имеют вид
; +; +; +;
т.е. в системе Штурма теряется одна перемена знаков.
Таким образом, функция S изменяет свое значение лишь при переходе через корень многочлена, причем она уменьшает свое значение на единицу.
Итак, S(a) S(b) равно числу корней многочлена f на отрезке [a; b]: Теорема доказана.
Непосредственно из леммы 1 и доказанной теоремы получаем Следствие. Число вещественных корней многочлена f(z) = a0zn +
a1zn 1 + + an с вещественными коэффициентами и имеющего простые корни равно S( b) S(b); где
b = 1 + max jakj:
12k n ja0j
Замечание. Из теоремы Штурма и еe следствия вытекает, что можно указать отрезок [ b; b] и такое его разбиение вида b b1 < < bm < b; что на каждом из отрезков [ b; b1]; [b1; b2]; : : : ; [bm; b] находится ровно один корень многочлена f . В этом случае говорят, что корни многочлена f отделены.
Это замечание позволяет ограничиться далее только рассмотрением многочлена f с единственным простым корнем x0 на интервале (a; b). Укажем способ приближенного вычисления корня x0; называемый методом линейной интерполяции.
Геометрически метод линейной интерполяции заключается в том, что функция f на отрезке [a; b] заменяется линейной функцией, соединяющей точки (a; f(a)) и (b; f(b)) (см. рис. 13). В качестве приближенного значения корня берется абсцисса точки пересечения линейной функции с осью абсцисс
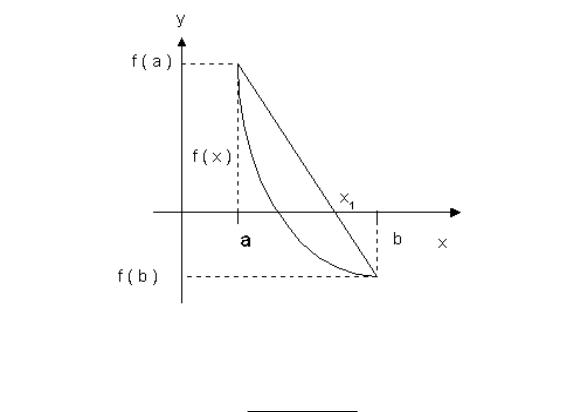
x 12: Приближенное вычисление корней многочленов |
79 |
Рис.13
т.е. число
bf(a) af(b) x1 = f(a) f(b) :
Если f(x1) 6= 0; то этот же прием применяется к интервалу [a; x1], если f(x1) < 0, и интервалу [x1; b], если f(x1) > 0: В результате получим последовательность (x1; x2; : : : ); сходящуюся к x0:
Упражнения к §12
1.Составьте ряд Штурма и отделите вещественные корни многочленов а) f1(x) = x3 3x 1; б) f2(x) = x4 2x3 + x2 2x + 1;
в) f3(x) = x4 x3 2x + 1:
2.Определите число вещественных корней многочлена f(x) = x3 + px + q, где p; q 2 R:
3.Укажите два последовательных приближения метода линейной интерполяции к вещественным корням следующих многочленов
a) f(x) = x3 10x 5; b) f(x) = x3 + 2x 30;
c) f(x) = x3 3x2 13x 7; d) f(x) = x3 3x2 x + 2:
4. Определите число вещественных корней многочлена
f(x) = x5 5ax3 + 5a2x + 2b; a; b 2 R:
80 |
Глава 2. Алгебраические объекты; Алгебра многочленов |
5.Пусть дан многочлен f(x) = x5 + 3x2 + 7: Какое утверждение ложно?
1)f не имеет положительных корней;
2)f имеет вещественный корень;
3)f не имеет рациональных корней;
4)сумма всех корней f отлична от нуля?

81
ГЛАВА Ш. ЛИНЕЙНАЯ АЛГЕБРА
x 13. Метод Гаусса решения систем линейных уравнений
Пусть K – некоторое поле. В этом параграфе излагается метод Гаусса построения решений системы линейных уравнений вида
a11x1 + a12x2 + + a1nxn = b1;
a21x1 + a22x2 + + a2nxn = b2;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (1)
am1x1 + am2x2 + + amnxn = bm;
где x1; x2; : : : ; xn 2 K – неизвестные, подлежащие определению (число их n не обязательно совпадает с числом m уравнений) и числа a11; a12; : : : ;
amn; b1; : : : ; bm принадлежат полю K . Числа a11; a12; : : : ; amn; называемые коэффициентами системы (1), часто записывают в виде прямоугольной таблицы
0
a11 a12
Ba21 a22
B... ...
@
am1 am2
:: : a1n
:: : a2n
... ...
:: : amn
1
C
C: (2)
C
A
Таблицу вида (2) называют матрицей размера m n с элементами поля K (безотносительно к системе уравнений (1)), состоящей из m строк и n столбцов. При фиксированном i (1 i m) упорядоченный набор (ai1; : : : ; ain) 2 Kn называется i - ой строкой матрицы. При фиксированном j(1 j n) набор (a1j; : : : ; amj) 2 Km называется j - ым столбцом матрицы. Числа aij; 1 i m; 1 j n называют элементами матрицы, где число i указывает на номер строки, а число j - на номер столбца, на пересечении которых стоит число aij . Если m = n (т.е.число строк равно числу столбцов), то матрица (2) называется квадратной (иногда "порядка n"). Числа a11; a22; : : : ; ann называются главной диагональю квадратной матрицы.
Определение 1. Упорядоченный набор ( 1; 2; : : : ; n) 2 Kn называется решением системы линейных уравнений (1), если каждое из уравнений обращается в тождество после замены в нем неизвестных xk соответствующими числами k .
Определение 2. Система уравнений (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
82 |
Глава 3. Линейная алгебра |
Совместная система называется определенной, если она имеет единственное решение и неопределенной, если она имеет, по крайней мере, два решения.
Пример 1. Система уравнений
x1 + x2 = 1;
x1 x2 = 3
определенна ((2; 1) 2 R2 – единственное решение этой системы). С другой стороны, система
2x1 x2 = 1;
4x1 2x2 = 2
имеет бесконечно много решений вида ( ; 2 1) 2 R2; 2 R: Определение 3. Две системы уравнений называются равносильными
или эквивалентными, если они имеют одно и то же множество решений. Отметим, что следующие два элементарных преобразования:
1) исключение из системы уравнений вида
0 x1 + 0 x2 + + 0 xn = 0; |
(3) |
2) прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое число, приводят к новой эквивалентной системе уравнений. Именно эти два типа преобразований лежат в основе метода Гаусса решения систем линейных уравнений, к изложению которого мы приступаем.
Метод Гаусса заключается в последовательном исключении неизвестных, и поэтому его также называют методом последовательного исключения неизвестных.
Если среди уравнений системы (1) есть хоть одно уравнение вида
0 x1 + 0 x2 + + 0 xn = b 6= 0; |
(4) |
то такая система уравнений несовместна.
Пусть теперь система уравнений (1) не содержит уравнений вида (3); иначе мы его отбросим и перейдем к другой эквивалентной системе.
Положим для определенности a11 6= 0 (в противном случае следует начинать с какого-нибудь другого ненулевого коэффициента из первого уравнения системы (1)). Оставив первое уравнение без изменения, исключим из всех уравнений системы (1), начиная со второго, неизвестное x1 . Для этого обе ча-
сти первого уравнения умножим на число a21 и вычтем из соответствующих
a11
частей второго уравнения, затем обе части первого уравнения, умноженные
x 13: Метод Гаусса решения систем линейных уравнений |
83 |
на число a31 , вычтем из соответствующих частей третьего уравнения и так
a11
до последнего уравнения. В результате таких преобразований получим эквивалентную систему уравнений
a11x1+ a12x2+ : : : +ainxn = b1; |
|
||||||
a0 x2 |
+ : : : +a0 |
xn |
= |
b0 |
; |
(10) |
|
22 |
: : : |
2n |
|
|
2 |
|
|
: : : |
: : : |
|
: : : : : : |
|
|||
as0 2x2+ : : : |
+asn0 |
xn |
= |
bs0 : |
|
||
В полученной системе уравнений (10) число уравнений s могло оказаться меньше, чем m; это связано с тем, что среди них могли оказаться уравнения вида (3), которые мы договорились отбрасывать. Если же среди уравнений системы (10) оказались уравнения вида (4), то нами была бы установлена несовместность системы (1).
Таким образом, среди коэффициентов второго уравнения есть отличные от нуля. Для определенности, пусть a022 6= 0: Систему уравнений (10) преобразуем, исключая из последних s 2 уравнений неизвестную x2 : вычитая из третьего уравнения второе, предварительно умноженное на a032 = a022; из четвертого уравнения - второе, умноженное на a034 = a022 и т.д. В итоге получим систему уравнений, эквивалентную системе (10) (и, следовательно, системе (1)), которая имеет вид
a11x1+ a12x2+ a13x3+ : : : +ainxn = b1;
a0022x2+ a0023x3+ : : : +a002nxn = b002; a0033x3+ : : : +a003nxn = b003;
: : : |
: : : |
: : : |
|
: : : : : : |
|
|
|
|
|
|||
a00 |
x |
+ : : : |
+a00 |
x |
n |
= b00 |
; |
l |
|
s |
|
m: |
l3 |
3 |
|
ln |
|
l |
|
|
|
|
|||
Продолжая такие преобразования далее, систему (1) преобразуем к следующей эквивалентной системе уравнений
c11x1+ c12x2+ c13x3+ : : : +c1kxk+ : : : +c1nxn c22x2+ c23x3+ : : : +c2kxk+ : : : +c2nxn
c33x3+ : : : |
+c3kxk+ : : : +c3nxn |
|
: : : : : : |
: : : : : : |
: : : |
|
ckkxk+ : : : |
+cknxn |
=d1;
=d2;
= d2; (100)
:: : : : :
=dk;
где k m и коэффициенты c11; c22; : : : ; ckk отличны от нуля. Заметим, что если в процессе проводимых преобразований системы (1) получим одно из уравнений вида (4), то система (1) несовместна.
При решении системы (1) возможны два случая
84 |
Глава 3. Линейная алгебра |
Случай k = n. Последнее уравнение системы (1) имеет вид cnnxn = dnn
и поэтому xn = dn=cnn . Подставив это значение в предпоследнее уравнение системы (100); получим равенство cn 1;n 1xn 1 + cn 2;nxn = dn 1; откуда находим значение xn 1 . Продолжая такой процесс, найдем xn 2; : : : ;
x1: Таким образом, система (1) в этом случае имеет единственное решение. Случай k < n: Из последнего уравнения системы (100) получаем, что
xk = 1=ckk(dk ck k+1 xk+1 cknxn):
Подставив это выражение для xk в предпоследнее уравнение, найдем выражение для xk 1 и т.д. В конце концов система (1) будет иметь вид
x1 = 1 k+1xk+1 + + 1nxn + 2;
x2 = 2 k+1xk+1 + + 2nxn + 2;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
xk = n k+1 xk+1 + + knxn + k:
Неизвестные xk+1; : : : ; xn называются свободными. Им можно придать произвольные значения и затем из последней системы найти значения неизвестных x1; x2; : : : ; xk . Итак, при k < n система (1) имеет бесконечное множество решений.
Суммируя все изложенное, получаем, что метод Гаусса применим к любой системе линейных уравнений и имеет место
Те о р е м а 1. 1) Система (1) несовместна, если в процессе преобразований получим уравнение вида (4), и совместна, если такие уравнения не встречаются.
2) Совместная система (1) будет иметь единственное решение (будет определенной), если она преобразуется к системе вида (100), где k = n:
3) Совместная система (1) будет иметь бесконечно много решений (неопределенной), если она преобразуется к системе (100), где k < n:
Сделанные выводы применимы к однородной системе линейных уравнений, т.е. уравнений вида (1), где числа bi; : : : ; bm; называемые свободными членами, нулевые. Однородная система всегда совместна, так как она обладает нулевым решением (0; 0; : : : ; 0):
Те о р е м а 2. Однородная система уравнений, в которой число уравнений меньше числа неизвестных, имеет бесконечное число решений.
x 14: Линейные пространства. Базисы |
85 |
Упражнения к § 13
1. Решите системы уравнений |
|
a) x1 3x2 + 2x2 = 1; |
b) x1 + x2 + x3 = 6; |
2x1 + x2 4x3 = 5; |
2x1 + x2 x3 = 1; |
5x1 8x2 + 2x3 = 8: |
3x1 + 5x2 3x3 = 4: |
x 14. Линейные пространства. Базисы
В следующем определении вводится в рассмотрение класс алгебраических структур, который играет основополагающую роль в линейной алгебре.
Определение 1. Множество X называется линейным (или векторным) пространством над полем K , если: 1) X – абелева группа (с аддитивной формой записи операции), 2) задан внешний закон композиции f : K X ! X ( x – обозначение для f( ; x)), причем выполнены следующие условия
a) 1x = x; b) ( + )x = x + x;
c) (x + y) = x + y; d) ( )x = ( x);
для любых чисел ; из K и любых элементов x; y 2 X:
Элементы линейного пространства обычно называют векторами. Наиболее важны - и только они будут рассматриваться - линейные пространства над полями R и C. Они, соответственно, будут называться вещественными и комплексными линейными пространствами. Слово "линейный"часто будет опускаться.
В геометрии примером линейного пространства является пространство (свободных) векторов плоскости или пространства.
Рассмотрим еще несколько примеров линейных пространств.
Пример 1. Пусть K – некоторое поле. Множество Kn упорядоченных наборов из n чисел поля K образует линейное пространство над полем K , если положить
x + y = (x1 + y1; x2 + y2; : : : ; xn + yn); x = ( x1; x2; : : : ; xn)
для любых x = (x1; x2; : : : ; xn); y = (y1; : : : ; yn) 2 Kn и любого числа2 K . Нулевым элементом в Kn служит набор 0 = (0; 0; : : : ; 0): Элементом, противоположным к элементу x = (x1; : : : ; xn); служит элементx = ( x1; : : : ; xn): Проверка аксиом линейного пространства проста (сделайте это !).

86 Глава 3. Линейная алгебра
В частности, само поле K = K1 является линейным пространством. Если K = R; то Rn – вещественное линейное пространство, и, если
K = C; то Cn – комплексное линейное пространство. Отметим еще линейное пространство f0; 1gn , играющее важную роль в теории кодирования (f0; 1gn состоит из наборов n чисел, равных нулю или единице).
Пример 2. Пусть Pn = Pn(K) – множество многочленов над полем K степени не выше n 0: В x 9 были определены операции сложения и умножения многочленов на комплексные числа. Нулевым элементом линейного пространства Pn служит нулевой многочлен. Таким образом, Pn – линейное пространство над полем K .
Пример 3. Каждая алгебра является линейным пространством. В частности, линейным пространством является алгебра многочленов, рассматриваемая в x 9:
Пример 4. Множество C[a; b] непрерывных вещественнозначных (или комплекснозначных) функций, определенных на отрезке [a; b]; образует вещественное (соответственно, комплексное) пространство. Алгебраические операции определяются следующим образом:
(x + y)(t) = x(t) + y(t); ( x)(t) = x(t)
для любого числа 2 R ( 2 C) и любых функций x; y из C[a; b]. Операция сложения функций определена корректно, так как сумма двух
непрерывных функций непрерывна. Нулевым элементом пространства C[a; b] служит тождественно равная нулю функция.
Пример 5. Множество Cw непрерывных и периодических, периода w > 0, функций является линейным пространством с алгебраическими операциями сложения и умножения на числа из поля K (K = R или K = C в зависимости от того, являются функции из Cw вещественнозначными или комплексными), определяемыми как и в примере 4. Следует только отметить, что x+y; x 2 Cw; если x; y 2 Cw и 2 K . Действительно, (x+y)(t+w) = x(t+ w)+y(t+w) = x(t)+y(t) = (x+y)(t) 8t 2 R; ( x)(t+w) = x(t) = ( x)(t):
Пример 6. Матрицы вида |
|
|
1 |
|
0 a11 |
a22 |
: : : a2n |
|
|
a11 |
a12 |
: : : a1n |
C |
|
B ... |
... |
... ... |
; |
|
B am1 |
am2 |
: : : amn |
C |
|
B |
|
|
C |
|
@ |
|
|
A |
|
обозначаемые также символом (aij); где a11; a12; : : : ; amn принадлежат полю K , образуют линейное пространство Matrm;n(K) (символом Matrn(K), если
