
Лекции по алгебре.Баскаков
.pdfx 5: Алгебраические операции.Группы |
37 |
13.Докажите, что если f и g – движения, то f 1 и f g также являются движениями.
14.Докажите, что в абелевой группе G множество элементов вида fg2 : g 2 Gg образует подгруппу в G.
15.Докажите, что если H1 и H2 – нормальные подгруппы из группы G и
|
H1 |
TH2 = feg; то элементы из H1 |
перестановочны с элементами из H2 . |
||||||
16. |
Найдите перестановку из Sn , обратную к перестановке |
||||||||
|
|
|
|
2 |
3 |
: : : |
n |
1 |
|
|
|
|
|
1 |
2 |
: : : |
n 1 |
n |
: |
17. |
Найдите перестановку f 2 Sn , для которой |
|
|||||||
|
а) f = f 1; |
б) f3 = e. |
|
|
|
|
|
|
|
18.Докажите, что гомоморфизм f : G ! S групп является инъективным отображением тогда и только тогда, когда Kerf = feg:
19.Докажите, что любые две группы, состоящие из трех элементов, изоморфны.
20.Пусть Z – группа целых чисел (по сложению). Какие из следующих отображений fk : Z ! Z; k = 1; 2; 3 являются гомоморфизмами группы
Z :
1)f1(m) = m + 1; 2)f2(m) = 2m; 3)f3(m) = m; m 2 Z:
Какие из гомоморфизмов являются изоморфизмами?
21.Пусть f : G ! S – гомоморфизм групп. Докажите, что образ f(G) отображения f является подгруппой группы S .
22.Пусть A – некоторая вершина правильного тетраэдра. Докажите, что множество самосовмещений тетраэдра, оставляющих неподвижной точку A, есть группа, изоморфная группе перестановок S3:
23.Докажите, что группа самосовмещений правильного тетраэдра изоморфна группе S4 .
24.Докажите, что множество всех самосовмещений куба, оставляющих неподвижной некоторую его вершину, есть группа. Опишите эту группу.
38 |
Глава 2. Алгебраические объекты; Алгебра многочленов |
25.Пусть G – группа и a – некоторый элемент из G. Докажите, что отображение f : G ! G; f(g) = a g a 1 является изоморфизмом группы
G.
26. Пусть G – группа. Докажите, что отображение f : G ! G; f(g) = g 1; g 2 G является гомоморфизмом группы G тогда и только тогда, когда G – абелева группа.
27.Докажите, что группа перестановок S(A) конечного множества A = fa1; : : : ; ang изоморфна симметрической группе Sn .
28.Найдите фактор-группы G=G0 и G=G, где G0 – подгруппа из G, состоящая только из единичного элемента e (G0 = feg):
29.Пусть f : G ! S – гомоморфизм групп. Докажите, что группа f(G) изоморфна фактор-группе G=Ker f:
30.Найдите (с точностью до изоморфизма) фактор-группу R=Z:
31.Докажите, что натуральное число (m 1)! + 1 делится на простое число m 2 N (указание: рассмотрите группу Z=mZ и докажите, что если G -
группа из m элементов, то gm = e 8g 2 G):
x 6. Группы перестановок
В этом параграфе более подробно остановимся на изучении группы S(An) перестановок конечного множества An = fa1; a2; : : : ; ang и, в частности, симметрической группы Sn = S(f1; : : : ; ng): Важность изучения групп перестановок связана с теоремой Кэли (см. теорему 8), в которой утверждается, что любая конечная группа изоморфна некоторой подгруппе группы Sn для подходящего n.
Т е о р е м а 1. Число Pn перестановок множества An равно n!. Доказательство теоремы проведем индукцией по числу n. Если
n = 1, то группа S(A1) состоит только из тождественного отображения. Поэтому P1 = 1!.
Пусть n > 1 и Pn 1 |
= (n 1)! для числа перестановок любого мно- |
||||||||||||||
жества, состоящего из |
n |
|
1 |
элементов (согласно |
индуктивного предполо- |
||||||||||
|
|
n |
|
|
|
|
|
|
|||||||
жения). Множество S(An) представим в виде объединения |
Mk |
взаимно |
|||||||||||||
пересекающихся подмножеств Mk = |
f |
|
2 |
|
k=1 |
|
|
|
|
|
|||||
|
|
g |
|
|
|
||||||||||
|
f |
|
S(An) : f(a1) = aSk |
; 1 |
|
|
k |
|
n: |
||||||
x 6: Группы перестановок |
39 |
Число элементов в каждом из этих множеств одно и то же и, следовательно, равно числу элементов множества M1 , которое, очевидно, равно числу перестановок множества fa2; a3; : : : ; ang; т.е. числу Pn 1 = (n 1)!: Поэтому Pn = n(n 1)! = n! Теорема доказана.
Определение 1. Пусть ' = (ak1 ; ak2 ; : : : akn) – некоторая перестановка множества An = fa1; : : : ; ang: Если найдется пара (ki; kj), такая, что i < j, но ki > kj , то будем говорить, что пара (aki; akj ) образует инверсию. Общее
число инверсий перестановки ' обозначим символом N('): Если N(') –
четное число, то перестановка называется четной, а если N(') нечетно, то
– нечетной.
|
2 |
3 |
|
1 |
4 |
||
Так, для перестановки ' = |
2 |
3 |
число N(') равно 5 и поэтому |
4 |
1 |
нечетная.
Определение 2. Символом sign : S(An) ! f1; 1g обозначим отображение из группы S(An) в группу f1; 1g (см. пример 3 из x 5), определенное формулой sign(') = ( 1)N('):
Определение 3. Перестановка ' 2 S(An), переставляющая только два элемента (остальные остаются на месте), называется транспозицией.
Так, транспозиции из Sn имеют вид |
|
1 |
: : : |
i |
: : : |
j |
: : : |
n |
; где |
1 |
: : : |
j |
: : : |
i |
: : : |
n |
многоточиями заменены числа, остающиеся на месте. Легко видеть, что sign(') = 1 для любой транспозиции ' 2 S(An):
Т е о р е м а 2. sign( ') = sign(' ) = sign(') 8' 2 S(An) и
для любой транспозиции :
Доказательство проведем для симметрической группы Sn; так как в общем случае оно проводится аналогично. Аналогично проводимому доказательству устанавливается равенство sign' = sign':
|
|
|
|
|
|
Пусть ' = |
|
1 : : : n |
– транспозиция из Sn , меняющая места- |
||
|
и |
||||
|
|
|
k1 : : : kn |
|
|
ми числа i и j. Тогда |
|
|
|||
' |
|
= |
1 2 : : : i i + 1 : : : j 1 j : : : n |
: |
|
|
|
k1 k2 : : : kj |
ki+1 : : : kj 1 ki : : : kn |
|
|
Вначале рассмотрим случай, когда j = i + 1: Ясно, что как в переста- |
|||||
новке ', так и в перестановке ' |
каждое из чисел ki; ki+1 образует одну |
||||
и ту же инверсию с числами, остающимися на месте. Если пара (ki; ki+1) не образовывала инверсии, то в новой перестановке ' появляется одна новая инверсия, т.е. число инверсий увеличивается на единицу. Если же эта пара образует инверсию, то в перестановке ' она не будет образовывать инверсию, т.е. число инверсий уменьшится на единицу. И в том, и другом случае
40 |
Глава 2. Алгебраические объекты; Алгебра многочленов |
|||||
получаем sign(' |
) = sign' = sign |
sign'; так как sign = 1: |
||||
Рассмотрим теперь общий случай. Транспозицию |
можно представить |
|||||
в виде суперпозиции |
= |
1 : : : m 1 |
m |
m 1 1 |
2(j i) 1 = 2m 1 |
|
транспозий |
1; 2; : : : ; m; |
m 1; : : : ; 1; где |
1 переставляет числа i и i + 1 |
|||
2 – числа i + 1 и i + 2 и т.д.
Наконец, транспозиция m будет переставлять местами числа j и j 1. Тогда sign ' = (sign ')( 1)2m 1 = sign ': Теорема доказана.
Т е о р е м а 3. Всякая перестановка ' 2 S(An); An = fa1; : : : ; ang может быть разложена в произведение (суперпозицию) транспозиций, причем число сомножителей четно, если она четна и нечетно, если ' – нечетная перестановка.
Доказательство проведем индукцией по числу n. Если n = 2, то S(A2)
a1 |
a2 |
; |
состоит из тождественной перестановки e и перестановки ' = a2 |
a1 |
являющейся транспозицией, причем, e = '2 = ' ':
Допустим теперь, что наше утверждение доказано для n 1 и докажем его для n.
Рассмотрим произвольную перестановку |
|
||||
' = |
ak11 |
ak22 |
: : : |
akn |
|
|
a |
a |
: : : |
an |
|
из группы S(An). Вначале предположим, что k1 6= 1 и '(am) = a1 при
m 6= 1: Тогда перестановку ' можно представить в виде ' = |
1 f супер- |
||||||||||||
позции перестановки f |
и транспозиции |
1; которые имеют вид |
|
|
: |
||||||||
1 = ak1 |
a2 |
: : : |
a11 |
: : : |
an ; f = |
a1 |
ak2 |
ak3 |
: : : |
ak1 |
: : : |
akn |
|
a1 |
a2 |
: : : |
ak |
: : : |
an |
a1 |
a2 |
a3 |
: : : |
am |
: : : |
an |
|
Ввиду свойства f(a1) = a1 , перестановку f по сути дела можно рассматривать как перестановку только n 1 элементов a2; : : : ; an; которую в силу индуктивного предположения, можно представить в виде суперпозиции транспозиций. Следовательно, это же верно и для '. Случай k1 = 1 в силу проведенных рассуждений очевиден. Теорема доказана.
Т е о р е м а 4. Отображение sign : S(An) ! f1; 1g является гомоморфизмом групп.
Доказательство. Пусть f; ' – две перестановки из S(An); которые в силу теоремы 3 можно представить в виде суперпозиций транспозиций f = f1 fm; ' = '1 'k и тогда f ' = f1 fm '1 'k: Из теоремы 2 получаем, что sign(f ') = ( 1)m+k = sign(f)sign('): Теорема доказана.
x 6: Группы перестановок |
41 |
Следствие 1. sign(') = sign(' 1); ' 2 S(An):
Утверждение следствия следует из равенств
sign(' ' 1) = sign(')sign(' 1) = 1:
Следствие 2. Множество четных перестановок из S(An) образует нормальную подгруппу.
Доказательство. Если f – четная перестановка и ' – произвольная перестановка из S(An), то sign(' f ' 1) = sign(')sign(f)sign(' 1) = 1:
Проверка того факта, что четные перестановки образуют подгруппу отнесены
вупражнение 10. Следствие доказано.
Квопросам о разложении перестановок в произведение транспозиций и определения их четности (нечетности) можно подойти несколько по-другому, используя следующие понятия.
Определение 4. Элемент x0 из множества X называется неподвижной точкой отображения ' : X ! X , если '(x0) = x0: Если же '(x0) 6= x0; то
x0 называется подвижной точкой отображения ': |
|
|
|
||||
Например, для перестановки ' = |
|
1 |
2 |
3 |
4 |
5 |
множество непо- |
1 |
3 |
5 |
4 |
2 |
|||
движных точек состоит из двух чисел 1 и 4, а числа 2,3 и 5 являются ее подвижными точками.
Определение 5. Перестановка ' 2 S(An) называется циклической или циклом, если для любой пары (a; b) подвижных точек из An существует такое натуральное число m, что 'm(a) = b: Число подвижных точек цикла называется длиной цикла.
Пример 1. Перестановка |
|
|
|
|
|
|
3 |
|
|
' = |
1 |
8 |
6 |
4 |
5 |
2 |
7 |
2 S8 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
является циклической, так как подвижными ее точками являются числа 2,3,6,8, причем ' переводит число 2 в 8, 8 в 3, 3 в 6, а 6 снова в 2. Длина цикла равна 4.
Отметим, что циклами являются транспозиции.
Непосредственно из определения циклической перестановки следует, что ее граф можно представить в виде объединения непересекающихся связных
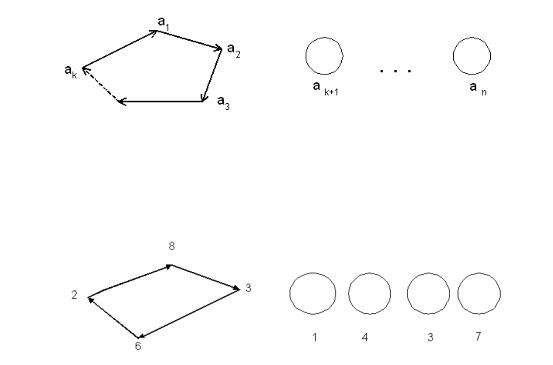
42 |
Глава 2. Алгебраические объекты; Алгебра многочленов |
графов вида
Рис. 10
Так граф, рассмотренной в примере 1 перестановки '; имеет вид
|
|
|
|
Рис. 11 |
|
|
|
Определение 6. Две перестановки '; |
|
2 Sn называются взаимно про- |
|||||
стыми, если их множества подвижных элементов не пересекаются. |
|||||||
Например, взаимно простыми будут перестановки |
|||||||
3 |
2 |
1 |
4 |
; 1 |
4 |
3 |
2 : |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
Лемма. Взаимно простые перестановки перестановочны. Доказательство. Пусть f; ' – две взаимно простые перестановки из
S(An) и a 2 An . Если a – неподвижная точка обеих перестановок f и ', то
(f ')(a) = f('(a)) = f(a) = a и аналогично (' f)(a) = a:
Пусть теперь b = f(a) 6= a и, значит, f(b) 6= b (иначе отображение f не инъективно). Следовательно, '(a) = a и '(b) = b: Тогда
(f ')(a) = f('(a)) = f(a) = b; (' f)(a)) = '(f(a)) = '(b) = b;
т.е. f ' = ' f: Лемма доказана.
Т е о р е м а 5. Каждую перестановку f 2 S(An) можно однозначно (с точностью до порядка сомножителей) представить в виде произведения взаимно простых циклов.

x 6: Группы перестановок |
43 |
Доказательство. Каждому элементу a из An поставим в соответствие множество ff(a); f2(a); : : : g, которое называется орбитой элемента a. То-
гда множество A подвижных точек из An представляется в виде объедине-
m
S
ния Mj взаимно непересекающихся множеств Mj; 1 j m, каждое
j=1
из которых является орбитой некоторого элемента из An , содержит более одной точки и поэтому f(b) 2 Mj 8b 2 Mj (см. упражнение 3). Сужение fj : Mj ! Mj перестановки f на каждое множество Mj (напомним fj(b) = f(b) 8b 2 Mj; см. определение 8 из x 3) является циклом и однозначно определяется перестановкой f . Каждую из перестановок fj расширим до некоторой перестановки fj : An ! An; положив fj(b) = fj(b) 8b 2 Mj и fj(b) = b 8b 2 Mi; i 6= j(fj называется расширением перестановки fj на An ).
Перестановки fj; 1 j m будут циклическими, и множество подвижных
точек для fj совпадает с множеством Mj . Поскольку fj(b) 2 Mj 8 b 2 Mj; 1 j m; то перестановки fj; 1 j m взаимно просты, причем f = f1
f2 fm (порядок их не играет роли ввиду перестановочности сомножителей; см. лемму). Теорема доказана.
Пример 2. Для перестановки
' = |
2 |
3 |
1 |
6 |
7 |
4 |
5 |
8 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
найдем разные орбиты. Имеем '(1) = 2; '(2) = 3; '(3) = 1; '(4) = 6; '(6) = 4; '(5) = 7; '(7) = 5; '(8) = 8: Таким образом, орбиты перестановки ' имеют вид: M1 = f1; 2; 3g; M2 = f4; 6g; M3 = f5; 7g: Сужения перестановки ' на эти множества являются перестановками вида
'1 |
= |
2 |
3 |
1 |
; '2 = |
6 |
4 |
; '3 |
= |
7 |
5 |
: |
|
|
1 |
2 |
3 |
|
4 |
6 |
|
|
5 |
7 |
|
Расширениями этих перестановок на множество A8 (см. доказательство теоремы 5) являются перестановки
'1 |
= |
2 |
3 |
1 |
4 |
5 |
6 |
7 |
8 ; '2 = |
1 |
2 |
3 |
6 |
5 |
4 |
7 |
8 |
; |
|||||||
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
|
|
|
|
'3 = |
1 |
2 |
3 |
4 |
7 |
6 |
5 |
8 : |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
|
|
|
|
Поэтому ' = '1 '2 '3 .
Теорему 5 можно сформулировать по-иному, используя следующее
44 |
Глава 2. Алгебраические объекты; Алгебра многочленов |
Определение 7. Подмножество G0 из группы G называется системой образующих группы G, если каждый элемент из G можно представить в виде произведения элементов из G .
Таким образом, имеет место Т е о р е м а 6. Множество всех циклических перестановок является
системой образующих группы перестановок S(An). Пусть
' = |
a2 |
: : : |
ak |
a1 |
ak+1 |
: : : |
an |
|
a1 |
: : : |
ak 1 |
ak |
ak+1 |
: : : |
an |
– некоторая циклическая перестановка. Тогда ее можно представить в виде произведения транспозиций '2 'k , где 'j 2 S(An) – транспозиция, переставляющая элементы aj 1 и aj; 2 j k. Отсюда, используя теорему 2, получаем, что sign(') = ( 1)k 1; где k – длина цикла '. Применяя теорему 4, получаем, что имеет место
Т е о р е м а 7. Транспозиции из группы S(An) являются системой
образующих этой группы, и для любой перестановки ' имеет место формула sign(') = ( 1)k1+ +km m; где k1; : : : ; km – длины взаимно простых циклов,
произведением которых является перестановка '; m – их число.
Пусть ' – перестановка из S(An). Тогда множество перестановок вида '; '2; : : : конечно, и поэтому существуют такие числа m; k; m < k; что 'k = 'm: Тогда e = ' k'k = ' k'm = 'm k , т.е. 'm k = e: Таким образом, для любой перестановки ' существует такое натуральное s, что 's = e: Этот факт оправдывает следующее
Определение 8. Пусть ' 2 S(An). Наименьшее из натуральных чисел m таких, что 'm = e; называется порядком перестановки.
Пример 3. Для циклической перестановки вида
' = |
a2 |
: : : ; |
ak; a1; ak+1 |
: : : ; |
an |
|
a1 |
: : : ; |
ak 1; ak; ak+1 |
: : : ; |
an |
порядок ее равен k, т.е. длине цикла.
Те о р е м а 8. Порядок перестановки ' 2 S(An), раскладывающейся
впроизведение взаимно простых циклов длины k1; : : : ; km соответственно, есть наименьшее общее кратное чисел k1; : : : ; km:
Доказательство. Согласно теореме 5, перестановку ' можно представить в виде взаимно простых циклов: ' = '1 'm . В силу леммы взаимно простые циклы перестановочны и поэтому имеет место равенство
'k = ('1 '2 'm) ('1 '2 'm) = 'k1 'k2 'km:
| |
|
{z |
|
} |
|
k |
раз |
|
|
x 6: Группы перестановок |
45 |
Из этого равенства следует (проверьте !), что 'k = e тогда и только тогда, когда 'kj = e 8j = 1; : : : ; m. Если перестановки '1; : : : ; 'm есть циклы длины k1; : : : ; km , соответственно, т.е. имеют порядок k1; : : : ; km , то наименьшее число k, для которого выполняются все равенства 'kj = e; 1 j m, равняется наименьшему общему кратному чисел k1; : : : ; km . Теорема доказана.
Т е о р е м а 9 (теорема Кэли). Каждая конечная группа G изоморфна некоторой подгруппе группы перестановок S(G) группы G.
Доказательство. Пусть G = fg0 = e; g1; : : : ; gn 1g: Каждому элементу g группы G поставим в соответствие перестановку ' = (g) 2 S(G) этой группы, определенную таблицей
|
' = (g) = |
gg00 |
gg11 |
gg22 |
:: :: :: ;; |
ggnn : |
|
|
g |
g |
g |
|
g |
Ясно, что |
(g1g2) = |
(g1) (g2); |
т.е. построенное отображение |
|||
: G ! S(G) |
является гомоморфизмом групп. Поскольку образ (G) го- |
|||||
моморфизма является подгруппой в S(G) (см. упражнение 21 из x 5) и поскольку – инъективное отображение (докажите !), то устанавливает биективное отображение между G и подгруппой (G) группы S(G). Теорема доказана.
Т е о р е м а 10 (теорема Лагранжа). Пусть G – конечная группа. Тогда для любой нормальной подгруппы H из G имеет место равенство
jGj = jHj jG=Hj;
где jSj обозначает число элементов конечного множества S .
Доказательство. Из леммы 2 x 5 следует, что имеет место равенство
m
S
giH = G; причем классы эквивалентности g1H; : : : ; gmH взаимно непе-
i=1
ресекаются, имеют одно и то же число элементов, равное jHj, и m = jG=Hj: Поэтому jGj = jHj jG=Hj. Теорема доказана.
Замечание. Нами сформулирован "ослабленный" вариант теоремы Лагранжа. В действительности в теореме Лагранжа (см., например, [9]) условия нормальности подгруппы H нет. В частности, отсюда следует, что число jGj делится на число jHj.
Определение 9. Группа G называется циклической, если существует элемент a 2 G такой, что для всякого элемента g 2 G существует целое число n 2 Z такое, что g = an .
Примером циклической группы являются группы Z и Zm: Ясно, что всякая циклическая группа абелева.
46 |
Глава 2. Алгебраические объекты; Алгебра многочленов |
Упражнения к § 6
1. Докажите, что подгруппа из S6 , состоящая из перестановок вида
1 |
2 |
3 |
4 |
5 |
6 |
; |
2 |
3 |
1 |
6 |
4 |
5 |
; |
3 |
1 |
2 |
5 |
6 |
4 |
; |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
4 |
5 |
6 |
1 |
2 |
3 |
; |
5 |
6 |
4 |
3 |
2 |
1 |
; |
6 |
4 |
5 |
2 |
3 |
1 |
; |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
изоморфна группе S3 .
2.Разложите следующие перестановки в произведение простых циклов и проверьте их четность (постройте графы этих перестановок)
'1 |
= |
4 |
3 |
2 |
5 |
1 ; '2 = |
5 |
6 |
1 |
4 |
3 |
2 |
; |
||||
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
'3 = |
7 |
9 |
3 |
1 |
5 |
8 |
4 |
2 |
6 : |
|
|
|
|||
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
3. Докажите указанные при доказательстве теоремы 5 три свойства
m
S
разложения An = Mj:
j=1
4.На стенах круглого зала картинной галереи висели картины. Как-то решили разместить их в другом порядке, меняя картины, которые висят рядом. Всегда ли можно с помощью таких перемещений разместить картины как задумано ?
5.Докажите, что перестановка ' четная, если ее порядок – нечетное число.
6.Найдите порядок следующих перестановок
a) |
3 |
5 |
7 |
9 |
6 |
8 |
1 |
2 |
4 |
; |
b) |
3 |
5 |
4 |
6 |
7 |
8 |
9 |
2 |
1 |
10 |
: |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
7.Какой наивысший порядок могут иметь перестановки на множестве, состоящем из а) пяти элементов, б) десяти элементов ?
8.Сколько существует перестановок 15-го порядка на множестве из 8 элементов ?
