
SalimovRB_matematika_gl_1-20_2011_web
.pdf
MM1 f x kx b . |
(3) |
Так как мы рассматриваем наклонную асимптоту, то считаем, что угол не равен  2. Это означает, что cos Пусть точка N – основание перпендикуляра, опущен-ного из точки M на асимптоту. Получили прямоугольный треуголь-ник NMM1 . Из него найдем выражение MN MM1 cos поэтому, учитывая, что cos , будем иметь
2. Это означает, что cos Пусть точка N – основание перпендикуляра, опущен-ного из точки M на асимптоту. Получили прямоугольный треуголь-ник NMM1 . Из него найдем выражение MN MM1 cos поэтому, учитывая, что cos , будем иметь
|
MM1 NM / cos . |
(4) |
Прямая y kx b есть асимптота линии |
y f x , следовательно, расстоя- |
|
ние MN от точки M до прямой стремится к нулю, когда точка M неограниченно удаляется от начала координат, т. е. её абсцисса x стремится к бесконечности.
Итак, MN 0 |
при x , значит, согласно (4) |
MM1 0 при |
x , |
т. е. |
|
lim MM1 0. |
Подставим сюда вместо MM1 выражение (3) и получим |
|
|
||
x |
|
|
|
|
|
|
|
lim f x kx b 0. |
|
(5) |
|
|
|
x |
|
|
|
Из (5) видно, что выражение под знаком предела – бесконечно малая функ-
ция, которую |
обозначим |
через p(x) . Тогда p( x) f x kx b |
или |
f (x) kx b p(x), |
где p(x) |
при x . Это соотношение поделим на x, |
пе- |
рейдем к пределу при x и учтем, что предел суммы есть сумма пределов. Получим
lim |
f x |
lim k lim b |
lim |
p(x) |
. |
|
|
||
|
|
|
|
||||||
x |
x |
|
x |
x x |
x |
x |
|
|
|
Поскольку 1 x 0 при x , |
произведение постоянной b на 1 x есть беско- |
||||||||
нечно малая величина, а её предел равен нулю. Аналогично |
lim( p(x) / x) 0. |
||||||||
|
|
|
|
|
|
|
|
|
x |
Предел постоянной k равен k, поэтому |
|
|
|
|
|
|
|||
|
|
|
|
|
k lim[ f |
x / x]. |
(6) |
||
|
|
|
|
|
|
x |
|
|
|
Соотношение (5) запишем так: lim f x kx b 0. Учтём, что слева предел
x
разности равен разности пределов и limb b. Поэтому
x
x |
|
f |
|
x |
|
kx |
|
x |
x |
|
f |
|
x |
|
kx |
|
b 0, |
|
|
lim |
|
|
|
|
lim b 0, |
lim |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
b lim |
f |
x kx . |
(7) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
141 |
5354.ru |
|
Итак, мы показали, что если линия y f x имеет наклонную асимптоту y kx b, то обязательно существуют два конечных предела (6) и (7) для чи-
сел k |
и b, входящих в уравнение асимптоты. И наоборот, если для линии |
||||||
y f x |
существуют два конечных предела (6), (7), то |
эта линия имеет |
|||||
наклонную асимптоту y kx b. В этом можно убедиться, |
проведя изложен- |
||||||
ные выше рассуждения в обратном порядке. |
|
||||||
Пример. Возьмём кривую с уравнением y f x , где |
f x x2 /(1 x). Эта |
||||||
кривая имеет вертикальную асимптоту с уравнением x 1. В самом деле, |
|||||||
lim[x2 /(1 x)] . |
|
|
|
||||
x 1 |
|
|
|
|
|
|
|
Найдём наклонную асимптоту этой линии. Вычислим сначала предел (6): |
|||||||
k lim |
f x |
lim |
|
x |
. Последний предел найдём по правилу Лопиталя, так как |
||
|
|
x |
|||||
x |
x |
|
x 1 |
|
|
||
здесь и числитель, и знаменатель стремятся к бесконечности. Получим
lim |
x |
lim |
x |
lim1 1. |
Итак, k 1. |
Теперь найдём предел (7): |
||||||
1 x |
1 x |
|||||||||||
x |
x |
x |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
x2 |
|
|
x |
|
|
|
|
|
|
b lim f x kx lim |
|
x 1 |
lim |
|
|
. |
|||
|
|
|
1 x |
|
|
|||||||
|
|
|
|
x |
x |
|
x |
1 x |
||||
Последний предел равен 1, следовательно, b 1. |
Зная k |
и b , запишем урав- |
||||||||||
нение наклонной асимптоты y x 1. |
|
|
|
|
|
|
||||||
§6. Общая схема исследования функций
ипостроения графиков
Общая схема исследования функции y f x заключается в следующем:
|
находим область определения функции и ее точки разрыва; |
|
отыскиваем сначала критические точки, в которых производная f x |
обращается в нуль или не существует; затем находим интервалы возрастания
и убывания функции, в которых f x сохраняет знак, |
точки максимума и |
минимума, максимальное и минимальное ее значения; |
|
определяем точки, в которых вторая производная |
f x обращается в |
нуль или не существует, затем находим интервалы выпуклости вверх и вы-
пуклости вниз функции f x , в которых |
f x сохраняет знак, и точки пере- |
гиба; |
|
142 |
5354.ru |
|

отыскиваем асимптоты кривой.
При построении графика целесообразно сначала изобразить асимптоты. Пример. Исследуем функцию y f (x) x2 /(1 x) . Имеем
f x x x 2 1 x 2 , f x 2 1 x 3 . Далее следуем вышеуказанной схеме.
Функция определена всюду, кроме точки x 1, |
которая является точкой |
||
разрыва, и f x при |
x 1. Областью определения является совокуп- |
||
ность интервалов ; 1 , |
1; . |
Производная f x обращается в нуль в |
|
точках x 2 и x 0 и не существует в точке x 1. |
Итак, критическими точ- |
||
ками являются x1 2, x2 1, x3 0. |
Ими определяются интервалы возраста- |
||
ния и убывания функции: |
; 2 , |
2; 1 , 1; 0 , |
0; . На них соответ- |
ственно f x 0, f x 0, |
f x 0, |
f x 0, т. е. |
f x сначала возрастает, |
потом убывает, опять убывает и снова возрастает. Точка x1 2 является точкой максимума, так как знак первой производной изменяется с «+» на «-»;
ymax f x x 2 4. Точка x2 1 не является точкой
экстремума, так как она – точка разрыва функции. Точка x3 0 – точка минимума функции f x , так как при переходе через неё первая производная из-
меняет знак с «-» на «+», и ymin f x x 0 0. Вторая производная f x не существует в точке
x 1; на интервале ; 1 она отрицательна, значит, кривая выпукла вверх, а на интервале 1; кривая выпукла вниз, так как здесь f x 0. Точка
x 1 не является абсциссой точки перегиба, поскольку функция в этой точке не определена. Кривая имеет асимптоты: вертикальную x 1 и наклон-
ную |
y x 1. График исследуемой функции пред- |
Рис. 75 |
|
ставлен на рис. 75.
143
5354.ru

ГЛАВА 8. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПРОИЗВОДНЫХ
§ 1. Производная длины дуги кривой
Пусть в плоскости Oxy задана кривая |
y f x (рис. 76), точка M0 с абс- |
||
циссой x0 – фиксированная точка кривой, а точка M с абсциссой x – пере- |
|||
менная точка. Введём понятие длины дуги части M0 M заданной кривой. Дугу |
|||
M0M разделим на n |
частей точками M1 |
, M2 |
, ... , Mn 1. Каждые две соседние точ- |
|
|
|
|
|
ки, включая M0 , M, соединим хордой и получим |
||
|
ломаную M0 M1M 2 ... M , соеди-няющую точки M0 |
||
|
и M и состоящую из n звеньев. Длину ломаной |
||
|
обозначим через ln. Число n всех звеньев устре- |
||
|
мим к бесконечности так, чтобы длины звеньев |
||
|
стремились к нулю. При этом вышеуказанная |
||
|
ломаная по форме будет приближаться к дуге |
||
Рис. 76 |
|
|
|
M0 M . Поэтому за длину дуги кривой M0 M есте- |
|||
ственно принять s limln. Так как M – переменная точка с абсциссой x, то с |
|||
|
n |
|
|
изменением положения точки M (с изменением абсциссы x |
этой точки) дли- |
||||||
на дуги s |
изменяется. Следовательно, эта дуга есть функция от x – абсциссы |
||||||
точки M . |
Обозначим ее s s x . |
|
|
|
|
|
|
На кривой возьмём точку M1 с абсциссой x x. |
На рис. 76 показан слу- |
||||||
чай, когда x 0. |
Длина дуги кривой |
|
получается из функции s x |
заме- |
|||
M0 M1 |
|||||||
ной x на x x, |
т. е. заменой абсциссы x |
точки M на абсциссу x x |
точки |
||||
M1. |
|
|
|
|
|
|
|
Итак, |
длина дуги кривой |
|
есть |
s x x . |
Длина |
дуги |
|
M0 M1 |
|||||||
|
s x x s x s |
– это приращение функции |
s x |
MM1 |
ствующее приращению x. Поэтому
lim s s x .
x 0 x
в точке x, соответ-
(1)
144
5354.ru

Точка |
M с абсциссой x |
кривой |
y f x |
имеет ординату |
f x , а ордината |
|||||||||||||
точки |
M1 |
равняется |
f x x . |
|
Тогда |
|
|
разность |
этих |
ординат есть |
||||||||
f x x f x y – приращение функции, |
соответствующее приращению |
|||||||||||||||||
x и вычисляемое для |
точки |
|
x , |
причем |
|
lim( y / x) yx . |
Из треугольника |
|||||||||||
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
||
MKM |
1 |
, у которого сторона KM |
1 |
y, |
получаем MM 2 x 2 |
y 2 . Это от- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
ношение разделим на x 2 и получим MM1 2 |
/ x 2 |
1 y 2 / x 2 . Отсюда |
||||||||||||||||
|
|
|
|
|
|
|
|
MM |
|
2 |
s |
2 |
|
y 2 |
(2) |
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|||||||
|
|
|
|
|
|
|
|
s |
|
|
x |
|
|
|
|
|
||
Будем считать, что кривая с уравнением y f x такова, |
что функция y f x |
|||||||||||||||||
имеет непрерывную производную |
f x . Можно показать, что для такой кри- |
|||||||||||||||||
вой (принимается без доказательства) имеет место условие |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
lim MM1 1. |
|
|
(3) |
||||
|
|
|
|
|
|
|
|
|
|
|
s 0 |
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M1 M |
|
|
|
|
|
|
|
Иначе говоря, предел отношения длины хорды |
MM1 , |
|
стягивающей дугу с |
|||||||||||||||
длиной s , |
к длине s |
этой дуги |
|
равен 1. |
В соотношении (2) перейдём к |
|||||||||||||
пределу, когда M1 M и |
x 0. |
Учтём, что слева предел произведения равен |
||||||||||||||||
произведению пределов. Справа предел суммы равен сумме пределов и предел квадрата (произведения) равен квадрату (произведению) пределов. В итоге имеем
|
lim |
MM |
1 |
2 |
|
|
s 2 |
|
|
y |
2 |
|
s |
|
lim |
|
1 lim |
. |
|||||
M1 M |
|
|
|
x 0 |
x |
|
x 0 |
x |
|
||
Слева первый предел согласно (3) равен 1, а второй предел равен s x |
со- |
гласно (1). Справа предел равен y x . Значит, s x 2 1 y x 2 , т. е. |
|
s x 1 yx 2 . |
(4) |
Получили формулу для вычисления производной длины дуги кривой s s x , когда эта кривая задана уравнением y f x .
§ 2. Кривизна кривой на плоскости
Пусть на плоскости Oxy задана кривая. Возьмем на ней дугу и в точ-
MM1
ках M, M1 проведём касательные к кривой (рис. 77). Угол , на который по-
145
5354.ru

ворачивается касательная к кривой в точке M1 , когда точка M1 стремится к
|
|
|
|
|
точке M , называется углом смежности дуги MM1. Отношение угла смежно- |
||||
сти |
|
|
|
|
к длине дуги MM1 |
|
|
|
|
|
|
|
(5) |
|
|
MM1 |
|
|
|
характеризует искривленность дуги |
|
данной дли- |
|
|
MM1 |
|
|||
ны. |
|
|
|
|
|
В самом деле, чем больше дуга |
|
искривлена, |
Рис. 77 |
|
MM1 |
|||
тем больше угол смежности и тем больше отношение (5). Например, для
|
|
|
|
|
|
дуги |
|
|
|
||
M M1 |
той же длины, что и дуга MM1 |
, угол смежности , так как дуга |
|||
|
|
|
|
|
|
|
|
|
|
||
M M1 |
искривлена больше, чем исходная дуга, и |
/ M M1 |
/ MM1. Но нас инте- |
||
|
|
ресует искривлённость не всей дуги MM1, а искривлённость кривой в точке |
|
M . Ясно, что чем ближе точка M1 к точке M, тем лучше отношение (5) ха- |
|
рактеризует искривлённость кривой в точке M . Ясно также, |
что искривлён- |
ность кривой в точке M наиболее полно характеризует предел отношения (5), |
|
когда M1 M. Этот предел называют кривизной кривой в точке M и обозна- |
|
чают K . Итак, |
|
|
(6) |
K lim [ / MM1 ]. |
|
M1 M |
|
Легко показать, что кривизна окружности радиуса R в любой её точке равна числу 1 R. Теперь получим формулу для вычисления кривизны кривой.
R. Теперь получим формулу для вычисления кривизны кривой.
Пусть |
на |
плоскости |
Oxy |
задана кривая |
|
|
y f x (рис. |
78) и функция f x имеет вторую |
|
|
|||
производную. В точке M этой кривой с абсцис- |
|
|
||||
сой x требуется вычислить кривизну K этой кри- |
|
|
||||
вой. Пусть на рассматриваемой кривой M0 – |
|
|
||||
фиксированная точка, а M – переменная точка с |
|
|
||||
абсциссой |
x. |
Длину дуги |
|
обозначим s x . |
|
|
M0M |
Рис. 78 |
|||||
|
|
|
|
|
||
На кривой возьмём точку M1 с абсциссой x x. Длина дуги |
|
|||||
M0M1 s x x . |
||||||
|
|
|
|
|
– приращение функции |
|
Поэтому длина дуги MM1 s x x s x s, где s |
||||||
s x в точке |
x , соответствующее приращению x. |
Поэтому |
lim( s / x) sx . |
|||
|
|
|
|
|
|
x 0 |
Известно, |
что вычисленная в точке x производная |
yx f (x) |
равна тангенсу |
|||
|
|
|
|
146 |
|
5354.ru |
|
|
|
|
|
|
|

угла , образованного с осью абсцисс касательной к кривой в её точке M с абсциссой x. Ясно, что этот угол будет изменяться с изменением абсциссы x точки M . Это значит, что есть функция от x , которую обозначим x . В
точке кривой M1 с абсциссой x x |
этот угол будет равен |
x x . Ясно, что |
|||||||||||||
разность x x x – приращение функции x |
в точке x, |
соответ- |
|||||||||||||
ствующее приращению x. Поэтому |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
lim[ / x] x. |
|
|
(7) |
|||
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
Из треугольника N1N2 N3 (см. рис. 78), образованного вышеука-занными каса- |
|||||||||||||||
тельными и осью Ox , видно, что x x x |
– угол между касатель- |
||||||||||||||
ными, следовательно, есть угол смежности дуги |
|
длина которой рав- |
|||||||||||||
MM1, |
|||||||||||||||
на s. |
Поэтому согласно формуле |
(6) (в которой |
нужно заменить на |
) |
|||||||||||
для K – кривизны кривой в точке M – имеем |
|
|
|
|
] lim[ / s]. В |
||||||||||
K lim [ / MM1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
M1 M |
|
x 0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
s 0 |
|
|
правой |
части и числитель, |
и |
знаменатель поделим |
на |
x, |
получим |
|||||||||
K lim |
x . Предел отношения равен отношению пределов, поэтому |
|
|||||||||||||
x 0 |
s x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K (lim x) / lim s x. |
|
|
|
|
|
|||||||||
|
|
x 0 |
|
|
|
x 0 |
|
|
|
|
|
|
|
||
Согласно (7) предел числителя равен x , |
а предел знаменателя равен sx . |
Сле- |
|||||||||||||
довательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
K x / sx . . |
|
|
|
(8) |
||
Но tg yx , следовательно, arctg yx . |
Возьмём отсюда производную по x, |
||||||||||||||
при этом учтём, что правая часть – сложная функция от x. |
Имеем |
|
|
||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
yx |
|
|
yxx |
. |
|
|
|
|
|
||
|
|
yx 2 |
|
|
|
|
|
|
|
||||||
|
1 |
|
x |
1 yx 2 |
|
|
|
|
|
|
|||||
Это выражение подставим в числитель (8), а в знаменатель запишем выражение (4) вместо sx . Тогда
yxx |
(9) |
K 1 yx 2 3 2 . |
Эта формула позволяет вычислить кривизну кривой в её точке M с абсциссой x, когда кривая задана уравнением y f x . Сказанное относится к любой
147
5354.ru

точке M, т. е. в каждой точке кривой будет своя кривизна K – функция от x
–абсциссы точки M . Иногда кривизну K считают величиной положительной
ив формуле (9) берут абсолютную величину правой части,
принимая, что в исходной формуле (6) угол смежности бе-
рётся без знака. Например, пусть |
2 |
, |
|
|
|
y x |
yx 2x, |
yxx 2. Фор- |
|
||
мула (9) даёт K 2 1 2x 2 3 2 . Эта формула определяет кри- |
|
||||
визну параболы с уравнением y x2 |
(рис. 79) в любой её точке |
|
|||
M с абсциссой x. Например, в начале координат (0.0) кривиз- |
Рис. 79 |
||||
на K 2. |
|
|
|
|
|
|
|
|
|
|
|
§ 3. Радиус, центр и круг кривизны кривой на плоскости
Пусть в плоскости Oxy задана кривая с урав- |
|
|||||
нением y f x , |
причем функция |
f x |
имеет вто- |
|
||
рую производную (рис. 80). Для этой кривой по |
|
|||||
формуле (9) найдем кривизну в точке M с абсцис- |
|
|||||
сой x. Будем считать, что K 0. |
|
|
|
|||
Радиусом кривизны этой кривой в точке M |
|
|||||
называется |
число, обозначаемое |
R |
и равное |
Рис. 80 |
||
R 1/ K, где |
K – только что найденная кривизна. |
|||||
|
||||||
В точке |
M |
проведём нормаль (прямую, перпендикулярную к касатель- |
||||
ной) в сторону вогнутости кривой. На этой нормали отложим отрезок MC R. Точка C называется центром кривизны кривой y f x для её точки M . Круг
радиуса R с центром в точке C называется кругом кривизны этой кривой для точки M . Ясно, что для каждой точки M будут свои радиус, центр и круг кривизны, т. е. с изменением положения точки M они изменяются.
148
5354.ru
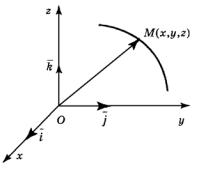
§ 4. Параметрические и векторное уравнения линии в пространстве
Пусть |
в пространстве |
Oxyz задана |
точка |
|
M x; y; z |
(рис. 81), а ее координаты представляют |
|
||
собой заданные функции некоторого аргумента t – |
|
|||
параметра, т. е. |
|
|
|
|
|
x x t , y y t , |
z z t . |
(10) |
|
С изменением t значения этих функций изменяют- |
Рис. 81 |
|||
ся, следовательно, изменяются координаты x, |
y, z |
|||
точки M , и эта точка описывает некоторую линию в пространстве. Соотно-
шения (10) называются параметрическими уравнениями этой линии. Каждое |
|||
из уравнений (10) умножим соответственно на базисные векторы |
i, |
j, |
k и |
сложим. Получим |
|
|
|
xi y j zk x t i y t j z t k. |
|
|
(11) |
Левую и правую части этого соотношения обозначим |
|
|
|
r xi y j zk. |
|
|
(12) |
r t x t i y t j z t k. |
|
|
(13) |
Тогда соотношение (11) запишется так: |
|
|
|
r r t . |
|
|
(14) |
Формула (14) называется векторным уравнением рассматриваемой кривой. Как видно из (12) и (13), выражение (14) есть радиус-вектор точки M,
начало которого всегда совпадает с началом координат, а его конец – точка M – описывает вышеуказанную линию.
Пример (винтовая линия). Пусть в системе координат Oxyz задан круговой цилиндр с образующими, параллельными Oz. Его направляющей служит расположенная на плоскости Oxy окружность радиуса a с центром в начале координат 0; 0; 0 . Пусть M x; y; z – произвольная точка цилиндра. Через неё проведём образующую, пересекающую плоскость Oxy в точке P. Пусть t есть угол, образованный радиусом OP с осью Ox. Этот угол отсчитывается от Ox и считается положительным, когда отсчёт ведётся против хода часовой стрелки,
149
5354.ru
если смотреть навстречу оси Oz, и этот угол считается отрицательным, если
он отсчитывается в противоположном направлении. |
|
Как видно из рис. 82, координаты точки P определяются формулами |
|
x a cos t, y a sin t. Такими же будут абсцисса и ордината точки M . |
Пусть ап- |
пликата z точки M выражается формулой z ht /(2 ), где h – заданное поло- |
|
жительное число. |
|
Итак, координаты точки M определяются формулами |
|
x a cos t, y a sin t, z ht /(2 ). |
(15) |
Ясно, что положение точки M зависит от значения t. При t 0 точка M совпадает с точкой P и находится на оси Ox. С увеличением t точка P движется по окружности, а точка M, находясь с ней на одной
образующей, движется по цилиндрической поверхности, поднимаясь вверх. При t 2 точка M окажется на плоскости Oxz на высоте z h. Эта линия называется винтовой. При неограниченном увеличении t точка M поднимается вверх, а когда t принимает отрицательные значения и стремится к ,
точка |
M винтовой линии уходит неограниченно вниз. |
Рис. 82 |
|
Ясно, что (15) представляют собой параметрические уравнения этой винтовой линии. Поступая, как ранее, запишем векторное уравнение винтовой линии в виде (14), где
|
|
|
h |
|
|
r |
t a cos ti |
a sin t j |
|
tk. |
|
2 |
|||||
|
|
|
|
§ 5. Предел и производная векторной функции скалярного аргумента
Введённое выше выражение
r t x t i y t j z t k |
(16) |
называется векторной функцией скалярного аргумента t. Пределом функции
(16) при t t0 , где t0 – заданное число, называется вектор, определяемый формулой
lim r t lim x t |
i lim y t |
j lim z t k. |
(17) |
|
t t0 |
t t0 |
t t0 |
t t0 |
|
150
5354.ru
