SalimovRB_matematika_gl_1-20_2011_web

векторами. Норма каждого из них равна единице, это видно из формулы (56).

n -мерном пространстве.

Как и в трёхмерном пространстве, каждой точке M x1 , x2 , , xn будем ставить в соответствие её радиус-вектор r x1, x2 , , xn , концом которого является точка M , а началом – точка O 0, 0, , 0 .

Пусть в n -мерном пространстве заданы точка M0 своим радиус-вектором r0 и ненулевой вектор a . Прямой в этом пространстве называется множество

точек, радиус-векторы которых определяются формулой r r0 at , где t – скаляр (параметр), который принимает любые действительные значения.

Пусть в пространстве заданы точка M0 своим радиус-вектором r0 и два

ненулевых вектора a и b , для которых не выполняются условия коллинеар-

ности a1 / b1 a2 / b2 an / bn .

Плоскостью в n -мерном пространстве называется множество точек, ра-

диус-векторы которых определяются формулой r r0 at bs , где t , s – дей-

ствительные скалярные величины, принимающие любые действительные значения.

Аналогично можно ввести понятие сферы в n -мерном пространстве.

§ 18. Поверхности второго порядка. Сфера. Цилиндр

Поверхностью второго порядка в пространстве Oxyz называется по-

верхность, определяемая уравнением второй степени относительно текущих

координат a11x2 a22 y2 a33z2 2a12 xy 2a13 xz 2a23 yz 2a14 x 2a24 y 2a34 z a44 0.

Здесь a11, a22 , ... – действительные числа, называемые коэффициентами. В зависимости от коэффициентов это уравнение может определять поверхность или точку (например, уравнению x2 y2 z2 0 отвечает точка O(0,0,0) ) или пару плоскостей (например, уравнению x2 y2 0 отвечает пара плоскостей

51

5354.ru

Рис. 32

Нетрудно проверить, что уравнение второй степени относительно x, y, z, в котором коэффициенты при x2 , y2 , z2 равны между собой, а члены с произ-

ведениями координат отсутствуют, представляет собой уравнение сферы (если не имеет место случай, когда это уравнение не определяет поверхность).

Цилиндры второго порядка. Цилиндрической

называется поверхность, описываемая прямой, остающейся параллельной некоторому направлению и пересекающей данную линию. Последняя называется

направляющей цилиндрической поверхности, а прямая

– образующей.

Пусть, например, образующие цилиндрической поверхности параллельны оси Oz и направляющей служит эллипс (рис. 33) в плоскости Oxy с уравнением

52

5354.ru

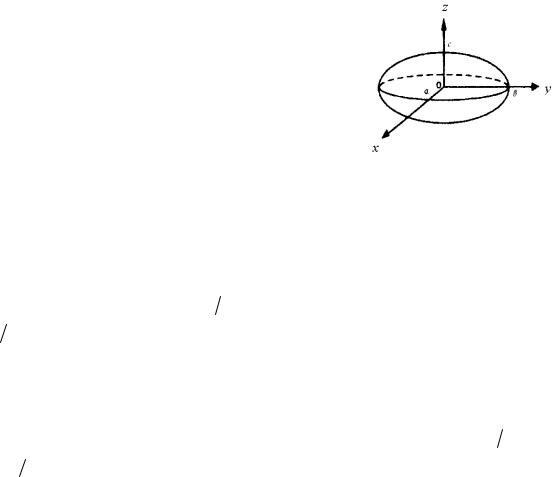
Эта поверхность называется эллиптическим цилиндром. Пусть M (x, y, z) – произвольная точка этого цилиндра, а точка K(x, y) – проекция M на плоскость Oxy. Ясно, что абсциссы и ординаты точек M и K совпадают. Так как точка K лежит на эллипсе, то её координаты x и y удовлетворяют уравнению (57). Но тогда этому уравнению удовлетворяют координаты x и y точки M цилиндра. Значит, (57) есть уравнение цилиндра.

Итак, уравнение (57) на плоскости Oxy определяет эллипс, а в пространстве Oxyz – эллиптический цилиндр с образующей, параллельной Oz, направ-

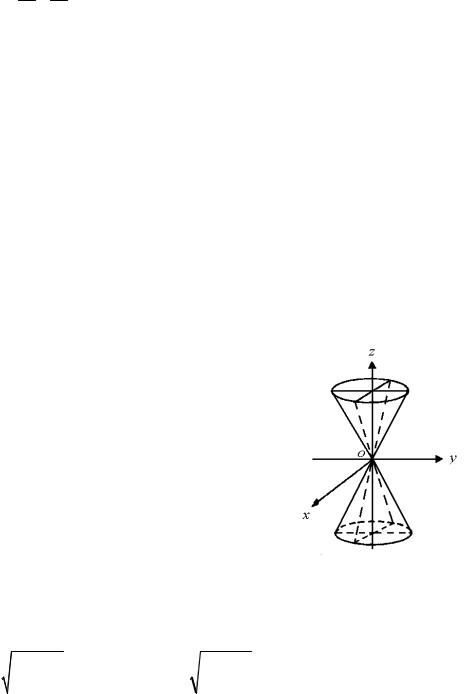
плоскости Oxy получаем эллипс наибольших размеров. При | h | c значения a1 и b1 достигают наименьших значений a1 0 и b1 0. Это означает, что плоскости z c и z c имеют с эллипсоидом по одной общей точке (0,0,c) и (0,0, c) соответственно. При | h | c эллипсоид с плоскостью z h общих точек не

При a b имеем эллипсоид вращения, поскольку в плоскости z h вместо эллипса получаем окружность. Эта поверхность получается при вращении

вокруг оси Oz эллипса ax22 cz22 1, расположенного в плоскости Oxz.

§ 20. Конус

Конусом второго порядка называется поверхность, определяемая уравнением

где a, b, c – заданные положительные числа (см. рис. 35). Исследовав форму

этой поверхности, как и эллипсоида, методом сечений, получим, что при сечении плоскостью z h ( h – постоянная) получается эллипс с полуосями a1 a | h |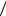c и b1 b | h |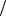c. Очевидно, что при h 0 a1 b1 0, т. е. конус (59) имеет с плоскостью Oxy одну общую точку – начало координат. С увеличением | h | значения a1 и b1 увеличиваются. Покажем теперь, что

при сечении поверхности (59) плоскостью с уравнением y kx ( k – постоянная), проходящей через Oz, получается пара прямых, проходящих через начало координат.

В самом деле, при таком сечении получается линия, определяемая системой уравнений

54

5354.ru

Поэтому последняя система равносильна совокупности двух систем

Все уравнения в этих системах определяют плоскости, проходящие через начало координат. Значит, каждая система определяет в пространстве прямую, проходящую через начало координат. При a b получаем конус вращения (вокруг оси Oz ).

§ 21. Однополостный и двуполостный гиперболоиды

Однополостный гиперболоид – это поверхность, определяемая уравнени-

ем

сечениях поверхности (60) плоскостью Oyz (с уравнением x 0 ) и плоскостью Oxz ( y 0 ) получаются гиперболы

y2 / b2 z2 / c2 1 и x2 / a2 z2 / c2 1

соответственно. Поверхность имеет вид, указанный на рис. 36. При a b по-

лучаем однополостный гиперболоид вращения ( Oz – ось вращения).

На рассматриваемой поверхности лежат семейства прямых, которые называются прямолинейными образующими. В частности, система уравнений

где k – произвольное заданное число, в пространстве Oxyz определяет прямую. Перемножив почленно уравнения системы, перейдём к уравнению (60). Следовательно, координаты любой точки M (x, y, z) этой прямой удовлетворяют уравнению (60), т. е. точка M принадлежит поверхности (60). Таким образом, прямая (61) лежит на поверхности. Изменяя значение величины k в системе (61), получим семейство прямолинейных образующих однополостного гиперболоида (60). Другое семейство прямолинейных образующих этого гиперболоида определяется системой

x / a z / c l(1 y / b),x / a z / c l 1 (1 y / b),

где l – произвольное число.

Двуполостный гиперболоид – это поверхность, определяемая уравнением

но. При a b получим двуполостный гиперболоид вращения ( Oz – ось враще-

ния).

§ 22. Эллиптический и гиперболический параболоиды

Эллиптический параболоид – это поверхность, определяемая уравнением

где p и q – заданные положительные числа. Расcекая поверхность (63) плоскостью z h ( h ), в сечении получим эллипс с полуосями 2hp и 2hq (см. рис. 38). Поверхность (63) пересекается с плоскостью Oxz ( y 0 ) по параболе x2 2 pz, а с плоскостью Oyz ( x 0 ) – по параболе y2 2qz. При p q получим

параболоид вращения ( Oz – ось вращения).

Гиперболический параболоид – это поверхность, определяемая уравнени-

ем

56

5354.ru

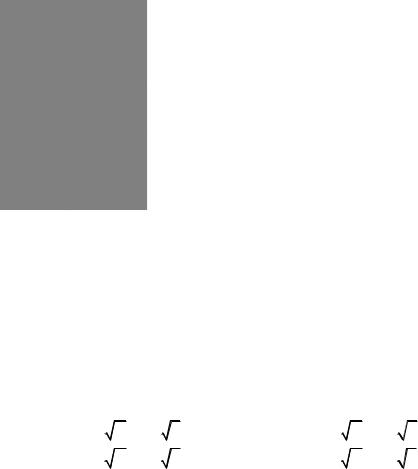
где p и q – заданные положительные числа. Поверхность (64) пересекается с

Рис. 39

Первое уравнение запишем так: y2 2q(z h2 /(2 p)). Оно определяет на плоскости x h параболу с ветвями, направленными в отрицательную сторону оси Oz, причём вершина параболы имеет координаты x h, y 0, z h2 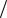(2 p). При

изменении h парабола (65) описывает поверхность, определяемую уравнением (64). Гиперболический параболоид содержит два семейства прямолинейных образующих, определяемых системами уравнений

где k и l – произвольные постоянные. Доказательство проводится так же, как и для однополостного гиперболоида.

57

5354.ru

ГЛАВА 3. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

§ 1. Определители высших порядков

Определитель четвёртого порядка содержит 16 элементов и обозначается

a11 a12 a13 a14

a21 a22 a23 a24 . a31 a32 a33 a34

a41 a42 a43 a44

Как и раньше, элементы этого определителя обозначаются aij , где i – номер

делитель третьего порядка, получаемый вычёркиванием строки и столбца, которым принадлежит элемент aij . Зная этот минор, определим алгебраическое

дополнение Aij для элемента aij определителя четвёртого порядка

Таким образом, определитель четвёртого порядка выражается через определители третьего порядка. Аналогично, с помощью определителя четвёртого порядка введём понятие определителя пятого порядка, шестого порядка и т. д. Зная определение определителя ( n 1)-го порядка, введём понятие определителя n -го порядка

Здесь A11, A12 , , A1n – алгебраические дополнения элементов первой строки a11, a12 , ..., a1n . Эти алгебраические дополнения по формуле (1) выражаются через миноры Mij для соответствующих элементов первой строки. Миноры –

определители ( n 1)-го порядка. Таким образом, определительn -го порядка выражается по формуле (3) через определители ( n 1)-го порядка. Соотношение (3) – разложение определителя n -го порядка по элементам первой строки.

58

5354.ru

Элементы a11, a22 , , ann определителя образуют его главную диагональ.

Можно показать (принимается без доказательства), что определитель раскладывается по элементам любой строки или любого столбца. Например, разло-

Таким образом, определитель равен сумме произведений элементов како- го-либо ряда (строки или столбца) на их алгебраические дополнения.

§2. Свойства определителей

1.Определитель не изменится, если его столбцы сделать строками с теми же номерами (эта операция называется транспонированием):

Доказательство этого свойства опускаем (оно основано на (4) и (5)).

2. Определитель лишь изменит знак, если поменять местами два какихлибо ряда (две строки или два столбца). Например,

В справедливости последнего равенства убедимся, разложив определители слева и справа по элементам соответственно первого и второго столбцов.

3. Определитель с двумя одинаковыми строками (столбцами) равен нулю. Чтобы доказать это свойство, достаточно переставить одинаковые ряды и

воспользоваться свойством 2.

4. Множитель, общий для элементов некоторого ряда определителя, можно вынести за знак определителя. Например, пусть – определённое число, тогда

59

5354.ru

Чтобы доказать это свойство, достаточно разложить определитель по элементам ряда, содержащим указанный множитель.

5.Если все элементы какой-либо строки (столбца) равны нулю, то определитель равен нулю. Это свойство доказывается разложением определителя по нулевым элементам соответствующей строки (столбца).

6.Если к элементам некоторого ряда (строки или столбца) прибавить соответствующие элементы другого ряда, умноженные на одно и то же число, то определитель не изменится:

Чтобы доказать это свойство, нужно разложить определитель в правой части по элементам первого столбца и учесть третье свойство.

7. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов другого параллельного ряда равна нулю. Например,

a11 A21 a12 A22 a1n A2n 0.

Рассматриваемое свойство доказывается разложением определителя по элементам второго ряда с последующей заменой его элементов на соответствующие элементы первого ряда.

Приведенные выше свойства для определителей третьего порядка доказываются проверкой.

§ 3. Матрицы и действия над ними. Обратная матрица

Числа a11, a12 , называются элементами матрицы. Коротко эту матрицу