SalimovRB_matematika_gl_1-20_2011_web

Теорема 3. Пусть функция y f x непрерывна в замкнутом интервалеa; b и величины m, M – соответственно наименьшее и наибольшее значения этой функции в интервале a; b . Тогда для любого числа заключённого

крайней мере в одной точке. На чертеже таких точек две, их абсциссы равны c и c. Ясно, что ординаты указанных точек графика f c и f c равны .

Таким образом, значение функция y f x принимает в точках c и c.

§ 2. Теоремы Ферма и Ролля

Теорема Ферма. Если функция f (x) определена в интервале (a,b), принимает в точке x c ( a c b ) своё наибольшее (наименьшее) значение в [a,b] и дифференцируема в точкеx c, то в этой точке производная f x обращается в нуль, т. е. f c 0.

Доказательство. Пусть f (c) – наибольшее значение. Возьмём точку c x,

В этих неравенствах перейдём к пределу при x 0 и согласно теории пределов (теорема 14 главы 4) будем иметь

121

5354.ru

дящему в предыдущие неравенства. Этот предел является обычным двусторонним и существует независимо от знака x . Следовательно, в двух предыдущих неравенствах пределы одинаковы и равны f c . Поэтому предыдущие

Теорема Ролля. Если функция y f x непрерывна в замкнутом интервале a; b , дифференцируема во всех внутренних точках этого интервала и, кроме того, на концах интервала принимает одинаковые значения, то в этом

значение функция f x примет в некоторой точке x c, лежащей внутри ин-

y f x в её точке с абсциссой c параллельна оси Ox. В самом деле, вычис-

122

5354.ru

ляемая в точке c производная f c равна тангенсу угла наклона к оси абсцисс касательной к кривой y f x в её точке с абсциссой x c. Если эта производная равна нулю, то f c tg 0 и 0, т. е. касательная параллельна оси Ox.

§ 3. Теоремы Коши и Лагранжа

Теорема Коши. Если функции f x и x непрерывны в замкнутом интервале a; b и дифференцируемы во всех внутренних точках этого интервала, причём всюду в этом интервале x 0, то в a; b найдется хотя бы одна точка x c ( a c b ), для которой справедлива формула

Она удовлетворяет следующим условиям:

непрерывна на a; b , действительно, x непрерывна в этом интервале по условию, поэтому произведение дроби и x также есть непрерывная

функция на этом интервале согласно теореме о произведении непрерывных функций;

разность, стоящая в правой части (4), – непрерывная функция согласно теореме о разности непрерывных функций;

F x дифференцируема во всех внутренних точках интервала a; b и

так как производные f x и x существуют согласно условию теоремы;

123

5354.ru

Но f x0 0 и x0 0. Следовательно, эта формула примет вид

Согласно условию теоремы существует предел отношения производных

что предел правой части существует. Тогда будет существовать и предел левой части, равный первому:

Сравнив формулы (9) и (10), придем к формуле (7). Теорема для указанного случая доказана. Случай, когда x , приводится к рассмотренному заменой

стремятся к нулю или к бесконечности при x x0 или x . Тогда к пределу отношения производных вновь можем применить правило Лопиталя, т. е.

следнего предела снова можем воспользоваться правилом Лопиталя. Поэтому

126

5354.ru

но этот предел не существует, так как при неограниченном изменении угла x, измеренного в радианах, функция принимает значения, заключённые между –1 и 1, следовательно, 1 cos x ни к какому пределу не стремится. Итак, предел отношения производных не существует. Однако предел (11) отношения функций существует. Убедимся в этом.

Предел (11) запишем так: Согласно теореме о пределе суммы он равняется сумме пределов, а предел постоянной равен ей самой.

является ограниченной функцией при x , так как sin x 1. Но произведе-

ние бесконечно малой функции и ограниченной функции есть снова бесконечно малая функция. Итак, предел в правой части последней формулы равен

Таким образом, предел (11) отношения функций существует и равен 1, в то время как предел отношения их производных не существует.

§ 5. Раскрытие неопределённостей

Всюду в настоящем параграфе будем рассматривать предел, когда

предел отношения lim[ f x / x ]. Чтобы найти этот предел, мы не можем воспользоваться теоремой о пределе частного, так как предел знаменателя ра-

127

5354.ru

вен нулю. Говорят, что здесь имеется неопределённость типа 00 . Эта не-

определённость раскрывается по правилу Лопиталя.

Пусть теперь f x , x одновременно стремятся к бесконечности, и требуется найти предел их отношения lim[ f x / x ]. Говорят, что здесь имеется неопределённость типа 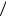. Эта неопределённость также раскрывается с

помощью правила Лопиталя. Рассмотрим другие виды неопределённостей. Требуется найти

0 . Эту неопределённость можно привести к одному из двух предыдущих

Получили неопределённость типа 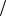. Для нахождения предела в правой части применим правило Лопиталя:

Здесь снова и числитель, и знаменатель стремятся к бесконечности при x 0, и для нахождения этого предела снова можно воспользоваться правилом Лопиталя. Тогда вновь придем к неопределённости , так как в числителе

появится дробь 1 x2 , а в знаменателе дробь 1 x3 . Этот процесс можно продолжать, никогда не доходя до конца. Поэтому к (14) правило Лопиталя применять не нужно, а достаточно просто преобразовать предел. Он будет равен

128

5354.ru

lim x . Искомый предел функции (13) также равен нулю. Таким образом,

x 0

lim x ln x 0.

x 0

Рассмотрим предел

Пока будем искать не сам предел A, а ln A. Согласно предыдущему соотношению имеем ln A ln lim f x x . Но логарифм, как основная элементарная функция, является непрерывной функцией, поэтому знак логарифма и знак предела можно переставить местами, и получим ln A lim ln f x x . В правой части воспользуемся свойством логарифмов: ln A lim x ln f x . Но здесь

ln A a, a – найденное число. Отсюда A ea .

Пример 2. Вычислить предел lim xx .

x 0

Здесь имеем неопределённость типа 00. Искомый предел обозначим через

129

5354.ru

ГЛАВА 7. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИИ ОДНОГО ПЕРЕМЕННОГО

§ 1. Возрастание и убывание функции

Функция называется возрастающей в интервале, если большему значению аргумента отвечает большее значение функции, а интервал называется

интервалом возрастания функции.

Функция называется убывающей в интервале, если большему значению аргумента отвечает меньшее значение функции, а интервал называется интервалом убывания функции.

Интервалы возрастания и убывания функции называются интервалами монотонности, а сама функция называется монотонной.

Ясно, что график возрастающей функции

Рис. 61

y f x на плоскости Oxy является восходящей

линией (рис. 61), так как ордината y f x точки графика функции увели-

чивается с увеличением абсциссы x этой точки (график убывающей функции является нисходящей линией).

Теорема 1 (необходимый признак возрастания и убывания функции).

Если дифференцируемая функция f x возрастает в интервале, то всюду в этом интервале f x 0 ; если она убывает в интервале, то всюду в нём