SalimovRB_matematika_gl_1-20_2011_web

2 / 2.

231

5354.ru

§ 10. Приближенное вычисление определенного интеграла методом трапеций

случаях определённый интеграл вычисляют приближённо. Рассмотрим лишь

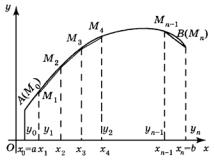
интеграл равен площади SaABb криволинейной трапеции, основание которой – отрезок ab оси Ox, а сверху она ограничена кривой AB с уравнением y f (x). Разделим интервал a, b на n равных частей длины x b a n, число n за-

точек кривой AB, абсциссы которых есть соответственно x0 , x1, x2 , ... , xn 1, xn . Обозначим точки

M 0 x0 , y0 , M1 x1, y1 , M 2 x2 , y2 , ... , M n 1 xn 1, yn 1 , M n xn , yn .

Каждые две соседние из них соединим хордой. Получим фигуру, состоящую из n трапеций, высоты которых одинаковы и равны x. Длины оснований трапеций равны y0 , y1, y2 , ... , yn 1, yn . Площадь фигуры Sn , состоящей из этих n трапеций, равна сумме площадей трапеций:

Sn x ( y0 yn ) / 2 y1 y2 ... yn 1 .

232

5354.ru

Ясно, что найдённую площадь Sn приближённо можно взять в качестве площади криволинейной трапеции SaABb , следовательно, приближённо можно принять ее равной искомому интегралу. В итоге получим формулу

Она называется формулой трапеций для приближённого вычисления опреде-

лённого интеграла. Чем больше число делений n, тем формула точнее. Пред-

лагаем самостоятельно, использовав ее, вычислить интеграл sin xdx, взяв

0

n 6.

233

5354.ru

ГЛАВА 13. КРАТНЫЕ ИНТЕГРАЛЫ

§ 1. Объём цилиндрического тела

Пусть на плоскости Oxy, в области D, задана функция двух переменных z f x, y , непрерывная и положительная всюду в D. В пространстве Oxyz уравнение z f x, y определяет поверхность. Так как f x, y 0 в области D, то указанная поверхность расположена выше плоскости Oxy (рис. 130).

Рис. 130

Требуется найти объем цилиндрического тела, основанием которого является область D, сверху оно ограниченно поверхностью с уравнением z f x, y , а с боков – цилиндрической поверхностью с образующими, парал-

лельными оси Oz и проходящими через границу области D.

Разобьем область D на n частей, которые будем называть частичными областями. Эти области и их площади обозначим 1, 2 , ... , i , ... , n .

Через границу каждой частичной области проведём цилиндрическую поверхность с образующими, параллельными оси Oz. Тем самым рассматриваемое цилиндрическое тело разобьём на n частей – цилиндрических тел. Внутри ча-

плоскости Oxy . На этой плоскости цилиндрическая поверхность, проведённая

234

5354.ru

через границу области i с образующими, параллельными оси Oz, отсечёт фигуру с площадью i (см. рис. 130). Таким образом получится цилиндр с площадью основания i , высотой f i , i , и, следовательно, объёмом, равным f i , i i . Этим цилиндром заменим i –ю часть цилиндрического тела с основанием i . Такое же построение выполним для всех частей области D, на которые мы её разбили. Тогда получим ступенчатое тело, состоящее из n цилиндров. Объём этого тела обозначим Vn . Он равен сумме объёмов цилиндров, из которых тело состоит:

между точками границы этой области. Например, для прямоугольника диаметром является длина диагонали, а для прямоугольного треугольника – это длина гипотенузы.

Обозначим через di диаметр области i . Пусть max di есть наибольший

Тогда вышеуказанное ступенчатое тело по форме будет приближаться к исходному цилиндрическому, поэтому естественно за объём V цилиндрическо-

области. Будем считать, что эта функция принимает любые значения. Область D разобьём на n частей с площадями , 2 , ... , n . Внутри области i возьмём произвольную точку Pi с координатами i , i и вычислим в ней значение заданной функции, т. е. найдём f i , i f Pi . Это значение умножим на площадь i i -й частичной области. Подобные вычисления проведем для всех частей, на которые разбили область D. Просуммируем все произведения,

235

5354.ru

стягиваются в точки. Тогда, если существует конечный предел вышеуказанной интегральной суммы и он не зависит ни от способа разбиения области D ,

(4) предел правой части (5) равен V – объёму соответствующего цилиндрического тела. Итак, объём цилиндрического тела, основанием которого служит

В этом заключается геометрический смысл двойного интеграла.

236

5354.ru

§5. Тройной интеграл и его механический смысл. Теорема существования кратных интегралов

Пусть в области V с границей S в пространстве Oxyz задана функция f x, y, z f P , где P(x, y, z) – любая точка области V (рис. 131).

операцию проделаем со всеми частями, на которые разбили область V , и, сложив все произведения, получим интегральную сумму для заданной функ-

раньше, di – диаметр области Vi , т. е. наибольшее расстояние между точками границы области Vi , и max di есть наибольший из всех диаметров частичных областей Vi области V .

Если существует конечный предел вышеуказанной интегральной суммы при n , max di 0 и он не зависит ни от способа разбиения области V , ни от выбора точек Pi i , i , i , то этот предел называют тройным интегралом по

Здесь dV называется элементом объёма, а остальные термины называют так же, как и в случае двойного интеграла. Поскольку область интегрирования расположена в системе Oxyz , принято dV dxdydz. .

Отметим частный случай. Формула (7), когда всюду в области

рования V . В самом деле, в этом случае правая часть формулы (7) под знаком предела содержит сумму всех объёмов частичных областей. Ясно, что эта сумма будет равна объёму области, и предел этого объёма тоже будет равен

V .

Рассмотрим механический смысл тройного интеграла. Пусть область V

сплошь заполнена веществом и mi – масса вещества, заключённого внутри объёма Vi , содержащего внутри себя точку Pi . Тогда предел lim( mi / Vi ), когда Vi 0 и стягивается в точку Pi , называется плотностью вещества в

характеризующая распределение плотности по телу, известна всюду в области V. Требуется найти M – массу вещества, заключённого в объёме V (массу тела V ).

Область V разобьем на n частей с объёмами V1, V2 , ... , Vn . Внутри области Vi (см. рис. 131) возьмём произвольную точку Pi i , i , i и найдём в ней значение заданной плотности, т. е. значение i , i , i . В силу малости части Vi приближенно можно считать, что внутри Vi плотность остаётся постоянной и равной i , i , i . Умножив эту плотность на объём Vi , найдём приближенно массу mi вещества внутри Vi . Это проделаем со всеми частями, на которые разбили область V. Сложив, приближенно найдем искомую

n

массу M : M i , i , i Vi . Ясно, что для нахождения точного значения M

i 1

x, y, z . Таким образом, масса определяется формулой

238

5354.ru

M x, y, z dxdydz.

V

Теорема (о существовании двойного (тройного) интеграла). Если функция непрерывна всюду в области включая границу, то существует конечный предел интегральной суммы для этой функции и области, в которой

§ 6. Свойства двойного (тройного) интеграла

Запишем эти свойства для двойных интегралов, для тройных интегралов они аналогичны.

1. Постоянный множитель можно вынести за знак двойного интеграла, т. е. если A const, то

Af (x, y)d A f (x, y)d .

D D

2. Двойной интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме двойных интегралов от слагаемых функций. Например, для двух функций

f (x, y) (x, y) d f (x, y)d (x, y)d .

которой справедлива формула

239

5354.ru

f x, y d f , S.

Для тройного интеграла свойства формулируются так же, только в свойствах 4 и 5 площадь S области D нужно заменить на объём области V . Эти свойства доказываются так же, как соответствующие свойства определённого интеграла с учётом определения двойного интеграла.

§ 7. Вычисление двойного интеграла

Пусть в области D на плоскости Oxy задана функция f (x, y) которая принимает положитель-ные значения всюду в области D (рис. 132).

Рис. 132

Тогда двойной интеграл от этой функции по области D, как мы знаем, ра-

Пусть область D лежит между прямыми x a и x b, параллельными оси Oy и имеющими общие точки с границей области D (это означает, что цилиндрическое тело лежит между плоскостями, перпендикулярными к оси Ox

240

5354.ru